Przeciwko liczbom rzeczywistym
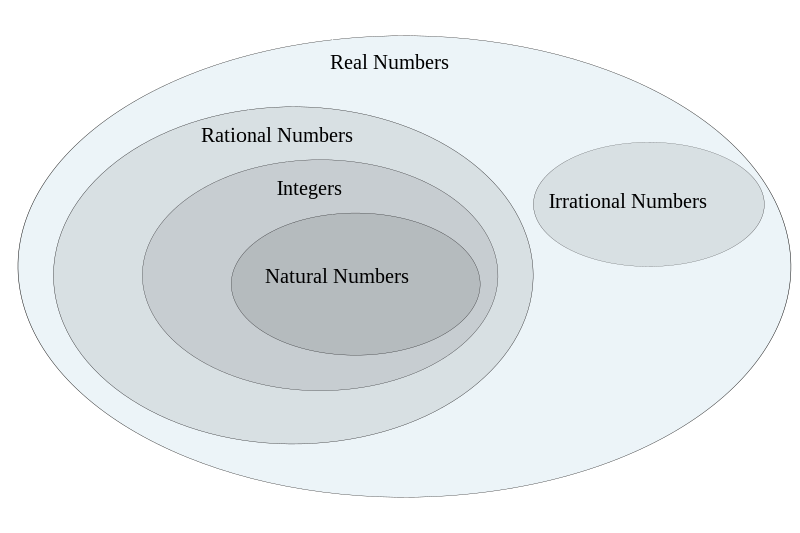
Pamiętamy ze szkoły kolejne zbiory liczb: naturalnych, całkowitych, wymiernych. Miło, przyjemnie, logicznie. A potem nie wiedzieć czemu zbiór liczb rzeczywistych. Będziecie ich Państwo bronić? A używaliście ich kiedykolwiek?
Naukę matematyki zaczynamy zwykle od liczb naturalnych N (na rysunku Natural Numbers), których używamy po prostu do liczenia. Definiuje się je nawet fachowo dosyć prosto (tzw. Aksjomatyka Peana): wprowadzamy pojęcia liczby 0 i liczby S następnej po danej liczbie (np. 3 jest następnikiem 2, 3 = S(2)), przy czym każda liczba ma następnik, 0 nie jest następnikiem żadnej liczby i jeśli liczby są równe, to ich następniki też. Zbiór po pierwsze zawierający 0 i po drugie mający taką właściwość, że jeśli zawiera liczbę a, to zawiera też jej następnik S(a), zawiera wszystkie liczby naturalne. To tzw. aksjomat indukcji – mówi on, że nasz zbiór zawiera 0, a skoro zawiera 0, to zawiera 1, a skoro zawiera 1, to i 2 – i tak do nieskończoności, by nie użyć stosowanego przez niektórych prawników ad mortum defecatum.
Jak teraz zdefiniować dodawanie? Dla dowolnej liczby naturalnej a suma a + 0 to dalej a, natomiast a + następnik b to następnik sumy a + b: (a + S(b) = S(a+b)). A więc a + 1 to a + S(0) = S(a+0) = S(a). Dodawanie 1 oznacza wzięcie następnika danej liczby, w ten sam sposób dodawanie 2 oznacza wzięcie następnika następnika itd. Z mnożeniem podobnie: a razy 0 daje 0, a razy S(b) daje a razy b dodać a: (a*S(b) = a*b + a). Proste.
To teraz zapytajmy, jaką liczbę należy dodać do a, żeby otrzymać c? Skoro a + x = c, to x otrzymamy, odejmując a od c. W ten sposób dochodzimy do odejmowania. Możemy teraz zapytać, co jeśli c jest mniejsze od a? Jaką liczbę dodać do 5, by otrzymać 3? Dlatego wprowadzono, dość późno, liczby ujemne. Jak je zdefiniować? Skoro chodzi nam o wynik odejmowania c – a, gdzie c jest mniejsze od a, to liczbę tą możemy zdefiniować formalnie jako właśnie tą parę liczb (c,a). Jak zdefiniować dodawanie takich par? Oczywiście (a-b) + (c-d) = (a+c) – (b+d). Z mnożeniem jest trudniej, ale po chwili namysłu piszemy (a-b)*(c-d) = (ac+bd) – (bc+ad).
No dobrze, ale zauważamy, że liczba ujemna 2-4 jest równa 6-8. A więc możemy utożsamić ze sobą wszystkie pary wyrażające tą samą różnicę (matematycy nazywają to klasą abstrakcji). Można też umówić się, by pisać np. zamiast 2-4 itd. zawsze 0-2, w sumie 0 można wywalić, przecież wiadomo, że 0 to nic, i pisać samo –2. Zauważamy dalej, że -a + a daje 0, więc -a jest przeciwnością a, i tak dzięki wprowadzeniu liczb ujemnych możemy odejmowanie zdefiniować jako dodawanie liczby przeciwnej. Tak otrzymaliśmy zbiór liczb całkowitych, Z (Integers). Ponieważ każdą liczbę naturalną n można przedstawić jako pewną parę n-0, zbiór liczb całkowitych obejmuje zbiór liczb naturalnych. Jednak liczb całkowitych jest dokładnie tyle, co naturalnych. Jeśli elementy danego zbioru możemy ułożyć w ciąg, to każdemu z nich można przypisać pewien numer, a więc liczbę naturalną. Skoro dla każdego znajdzie się jedna liczba naturalna (i dla każdego inna), to elementów jest tyle samo, co liczb naturalnych. Ciągiem będzie choćby 0, 1, -1, 2, -2…
Tak samo jak z odejmowaniem możemy postąpić z dzieleniem. Przez jaką liczbę należy pomnożyć a, by otrzymać c? Przez c/a. Zauważamy, że pytanie ma sens, o ile a nie jest równe 0, bo 0 pomnożone przez cokolwiek i tak da 0. To c/a rozumiemy jako dzielenie c przez a i tak samo możemy spytać o wynik dzielenia, gdy c nie jest wielokrotnością a. Tak wprowadzamy liczby wymierne jako kolejne, inaczej rozumiane pary liczb a/b. Definiujemy działania (tym razem mnożenie idzie łatwo: a/b razy c/d to po prostu ac / bd, zauważamy przy okazji, że a/b będzie równe ka / kb (matematycy znowu będą gadać o klasach abstrakcji), z dodawaniem radzimy sobie, zauważając, że a/b + c/d = (ad + bc) / bd. Otrzymane w ten sposób liczby nazywamy wymiernymi Q (jak ang. quotient, na rysunku Rational Numbers). Jako że każda liczba całkowita c = c/1, zbiór Z zawiera się w Q.
Szkoła proponuje dalej fascynujący przeskok do liczb rzezcywstych R (Real Numbers). Po co? Ano – tłumaczy – istnieją liczby niewymierne, i już starożytni Grecy to wiedzieli (a nawet próbowali ukryć, jako że burzyło to ich obraz świata). Przekątna kwadratu o boku 1 jest liczbą niewymierną, długość okręgu o promieniu 1 jest niewymierna. Wracając do równań – nie potrafimy dalej rozwiązać x*x = 2. I dlatego potrzebujemy liczby rzeczywistych – mówi szkoła. Nie potrafimy ich zazwyczaj zapisać, ale pokłońcie im się, są potrzebne.
A jak je zdefiniować? Można to zrobić, wszak matematycy ich używają. Choćby za pomocą przekrojów Dirichleta. Opis, jak to zrobić, zająłby pewnie tyle, co cały ten wpis. Nie da się tego zrobić w żaden prosty, intuicyjny sposób. A czy potrafimy ich używać? Dodawać, mnożyć? Dość słabo, skoro większości z nich nie jesteśmy w stanie zapisać nawet. Tak, jest ich znacznie więcej niż liczb naturalnych czy wymiernych (tego już dzieciom w szkole nie powiedzą). A pozwalają chociaż na rozwiązanie wszystkich równań? A guzik, weźmy x * x = -1.
Ale ich używamy… Chwila, jakich liczb niewymiernych używamy? Pierwiastków – istotnie. Ponadto π i e. To wszystko. Dwie ostatnie liczby możemy po prostu dołączyć do liczb wymiernych. To się fachowo nazywa rozszerzeniem ciała (czyli zbioru z dwoma działaniami o właściwościach dodawania i mnożenia). Ktoś powie: w logarytmie naturalnym ich używamy, a tego rozszerzenie ciała nie rozwiąże. W teorii istotnie, w praktyce używamy przybliżeń wymiernych.
Co zaś z nieskończoną liczbą pierwiastków? Istnieją tzw. rozszerzenia algebraiczne, a więc rozszerzenie o liczbę będącą rozwiązaniem (pierwiastkiem) pewnego wielomianu o współczynnikach z tego ciała. Tylko że rozszerzenie ciała nie musi być skończone. Istnieje w końcu domknięcie algebraiczne danego ciała, będące jego rozszerzeniem o wszystkie pierwiastki wszystkich takich wielomianów.
Elementy tegoż ciała nazywamy liczbami algebraicznymi. Zawierają się tu wszystkie pierwiastki we wszelkich kombinacjach, w tym także liczba będąca rozwiązaniem równania x*x = -1 zwana i. Po wprowadzeniu kilku dodatkowych założeń dalej potrafimy podać zasady wykonywania podstawowych działań. Dowód byłby nieco dłuższy, ale liczb algebraicznych jest tyle samo co naturalnych (bo i samych wielomianów o współczynnikach wymiernych jest tyle samo). Żadnych paradoksów nieskończoności, choć niektórych liczb algebraicznych zapisać prosto nie umiemy (np. rozwiązania x^5 + x = -1).
Tutaj jednak ktoś obeznany z matematyką powie: tylko że bez ciągłości zbioru liczb rzeczywistych nie sformułujemy rachunku różniczkowego i całkowego. Być może. Ale zagadnienia te wymagają tylko istnienia liczb rzeczywistych, nie zaś jakiegokolwiek ich użycia. Ponadto kto dzisiaj uczy całek w szkołach? Pochodnej większość uczniów nie zazna. Po co więc męczyć dzieci, zwłaszcza w podstawówce, liczbami rzeczywistymi? A z drugiej strony czemu nie, od kiedy szkoła uczy rzeczy przydatnych?
Marcin Nowak
Ilustracja: Damien Karras, Real Numbers, za Wikimedia Commons, w domenie publicznej
Komentarze
Gdybym byl nauczycielem matematyki w szkole podstawowej, to na pierwszej lekcji w klasie, w ktorej po raz pierwszy rysuje sie os liczb rzeczywistych powiedzialbym tak:
kochane dzieci, czy uwierzycie, ze na tej osi, ktora biegnie bez konca w obie strony jest tyle samo punktow ile na odcinku [0 1] tejze osi?
Przy spodziewanym chorze odglosow niedowierzania i chichotu wykazalbym ten fakt stosunkowo prostym rysunkiem na tablicy (czy dzis w szkolach sa jeszcze kreda, linial i tablica?)
Na koniec, kiedy juz dzieci naocznie(!) przekonaly sie, ze to ‚rzeczywiscie’ prawda, i ochlonely troche z wrazenia, zastapilbym (w ich glowach) odcinek [0 1] dowolnie malym odcinkiem osi…z tym samym rezultatem i byc moze spokojniejsza reakcja uczniow.
Matematyka to m. in. szkola wyobrazni a tej dzieci maja w nadmiarze… do zabicia?
Przypomniała mi się taka autentyczna historyjka sprzed ponad 50 lat.
Graliśmy sobie w piłkę „fuchą” ( czy ktoś jeszcze pamięta, co to było?) na placu i na rowerze przejeżdża obok pan Jasiu – urzędnik magistracki. Zatrzymał się i nawiązał z nami rozmowę mówiąc – ” Wos tam w szkole uczom jakiś iksów, piksów a w życiu wystarczy dodawanie, odejmowanie, mnożynie, dzielynie i procynty”
kaesjot,
nawet tego nie trzeba umiec jak sie ma kalkulator. Wystarczy, by np. robic fortuny z wyksztalceniem podstawowym.. i checia szczera.
A w życiu … 2+2= … a pan kierownik ile chce żeby było … Tak sobie myślę prywatnie … o rzeczywistości …
Cytuję: „wprowadzamy pojęcia liczby 0”, ale wtedy zaczynają sie problemy z dzieleniem przez zero, nieskończonościami etc, a co dowodzi, że matematyka nie ma w rzeczywistości NIC wspólnego z racjonalnym, naukowym myśleniem, że jest ona rodzajem religii (sytemu wiary), opartej na aksjomatach, które są nadane z góry i które są z definicji niepodważalne, nawet, jeśli prowadzą one do logicznych sprzeczności, tak jak w przypadku idei zera czy idei nieskończoności.
Poza tym, to 0 czyli zero, to NIE jest nic, gdyż jest ono zerem, a więc czymś zdecydowanie różnym od niczego.
Liczby niewymierne są zaś tylko pseudo-problemem dla matematyków, gdyż w praktyce wystarcza nam w ponad 99% przypadków przybliżenie liczby pi czy e do dwóch cyfr po przecinku, tak samo jak wystarczają nam w praktyce przybliżone rozwiązania złożonych równań różniczkowych, dla których obecnie nie istnieją rozwiązania dokładne w takim sensie, jak równanie nie 2+x=3 ma, jako rozwiązanie, dokładnie liczbę 1a nie około 1.
Dalej – rachunek różniczkowy i całkowy oparte są de facto na dzieleniu przez zero, tyle, że matematycy nauczyli się to zero dość sprytnie ukrywać pod postaciami „dążenia do zera”. Np. różniczkę funkcji nazywa się częścią główną (liniową) przyrostu funkcji: różniczka jest funkcją liniową przyrostu DELTAx i choć błąd oznaczany, jako epsilon może nie być liniowy, to dąży on szybko do zera, gdy DELTAx dąży do zera. Ale co to znaczy „dąży do zera”? Jak blisko zera może być ta DELTAx, aby nie być zerem i aby wiec mogła ona być w mianowniku?
@SŁOWIANIN STANISŁAW
Słyszałeś tę anegdotę o konkursie na Gł. Księgowego we firmie ?
Pytanie komisji rekrutacyjnej brzmiało – ile jest 2×2
Wgrał kandydat, który odpowiedział – a ile Państwo sobie życzą ?
Firmie, w której była taka właśnie Gł. Księgowa Urząd Skarbowy po kontroli naliczył ponad 1 mln zł zaległych podatków.
Czy im się to opłaciło ?
Zdefiniowanie różniczki bezpośrednio, jako rodzaju pochodnej kierunkowej:
df (x,h) = lim (f(x+th) – f(x))/t gdzie t -> 0 czyli gdzie ‘t’ dąży do zera. Czyli że mamy de facto dzielenie przez zero, gdyż jak w praktyce odróżnimy liczbę bardzo bliską zeru, np. 1/10**1000000 od „prawdziwego” zera?
kaesjot 18 CZERWCA 2022 12:21
Otóż to. Jesli można zdefiniować za Einsteinem arytmetykę, gdzie 1+x=1, jeśli x=c, czyli szybkość światła w próżni, to można też zdefiniować arytmetyki, gdzie 2 razy 2 jest więcej albo mniej niż cztery. Poza tym, to księgowość jest arbitralnie przyjętym systemem rejestracji wydarzeń gospodarczych wyrażonych w pieniądzu, ale że obecnie pieniądz oparty jest na kredycie, czyli na czymś mniejszym od zera, to nie takie cuda jak 2*2>4 można w niej dziś wyczyniać. ;-)
kaesjot 18 CZERWCA 2022 12:21
Oplaciło, jeśli są oni dziś np. w Brazylii…
Czas przejscia fotonu przez molekule wodoru:
247 zeptosekund. Jedna zeptosekunda to 10 do potegi – 21 sekundy.
daleko to do czasu Plancka ok. 5.391 × 10 **-44
act 18 czerwca 2022 11:13
Nie każdemu jest on potrzebny. Mój wnuk gdy jeszcze chodził do przedszkola spytał mnie, ile mam lat. Odpowiedziałem mu że urodziłem się w 1954. A ile lat babcia – pyta dalej. Jest ode mnie 3 lata młodsza – odpowiedziałem. A teraz mamy 2021? – upewnił się. Potwierdziłem. Pomruczał sobie coś pod nosem i po chwili mówi – razem macie 131 lat. Po chwili mówi – a wszyscy mamy 222 lata !
Wszyscy czyli kto ? – pytam.
No ty, babcia, mama, tata, mój brat i ja !
Zgadzało się !
@kaesjot, 11:04:
Lata temu i urzędnik? Ja kilka tygodni temu słyszałem młodzież dyskutującą, że uczą się w szkole głupot, bo komu potrzeba czegoś więcej z matematyki niż dodawania i odejmowania, no, ewentualnie — tu młodzież się zawahała — procentów.
PS.
Młodzież, wyciągającą komórki i uruchamiający kalkulator, by dodać dwie liczby jednocyfrowe, też już widziałem.
@rem:
Hm… jako informatyk używam „liczb rzeczywistych” w pewnym przybliżeniu. I mam wrażenie, że ta świadomość, że używam pewnego „ziarnistego przybliżenia”, jakieś „ciągłej rzeczywistości” jest bardzo przydatna.
No, ale „jako informatyk”. Tu pojawia się wielkie pytanie, czego ma uczyć szkoła. Mamy przykład tej młodzieży, cytowanej w odpowiedzi do kaesjota, której się nie chce i która żyje w świecie gardzącym wiedzą. Przynajmniej taką, która nie daje się łatwo spieniężyć.
Po drugiej stronie jest ideał edukacji, pod którym bym się podpisał — szkoła, która ma dać podstawy poznania i zrozumienia świata, świadomego i krytycznego podejścia do rzeczywistości. O możliwości dalszego kształcenia się nie wspominając… Tu się przydają różniczki i całki, tak jak filozofia, czy jakaś aplikacja studiów genderowych.
Podobno 80% populacji ma problemy z podstawowa arytmetyka.
Ja, na szczescie, jestem w tej drugiej polowie.
Liczby rzeczywiste … to rachunki … Tak sobie myślę prywatnie … w takim ciągu od do pierwszego …
Nauczyciel do ucznia:
daje ci 10 zlotych i ojciec ci daje 10, to ile masz razem?
Uczen: no to mam 10.
Nauczyciel: siadaj pala, ty w ogole nie znasz podstawowych dzialan!
Uczen: taaak, to pan nie zna mojego ojca!
Ćwiartka i ćwiartka to pół litra … odpowiada Jasiu … Tak sobie myślę prywatnie … przyziemność domowa …
act 18 CZERWCA 2022 12:54
Bliskie zero, ale wciąż nie zero…
Czas Plancka – jednostka czasu w naturalnym systemie jednostek, oznaczana jako Tp = Lp/c = SQRT (dG/c**5) = 5,39116(13)*10**(-44) sekundy
gdzie:
Lp – długość Plancka, czyli 1,616229(38)*10**(-35) metra,
c – prędkość światła w próżni, czyli 299792458 metra na sekundę,
d – zredukowana stała Plancka = h/2*PI =1054571817*10** (-34) Js= 6,582119569 *10**(-16) eV s (jest ona kwantem momentu pędu, a więc tym samym i spinu i z tego też powodu przez wielu fizyków uważana jest za stałą bardziej podstawową niż sama stała Plancka. Oznaczenie to wprowadził brytyjski fizyk Paul A.M. Dirac.)
h – stała Plancka, czyli 6,62607015* 10** (-34) kg m**2 s**(-1)
G – stała grawitacji, czyli = 6,67430(15)*10**(-11) m**3/kg s**2 (zgodnie z prawem powszechnego ciążenia Newtona, dwa ciała punktowe, czyli takie, że ich wzajemna odległość jest większa od ich własnych rozmiarów) o masach m1 i m2 a odległe o r, działają na siebie z siłą, której wartość wynosi F=G(m1*m2)/r**2
SŁOWIANIN STANISŁAW 18 CZERWCA 2022 14:51
A ile setek wchodzi do pół litra?
act 18 CZERWCA 2022 14:02
Twoja mieć mnostwo za bardzo problemy z podstawowa polska języka.
kalvarya01 14:53,
ja wpadlem tylko na jedno piwo a Ty mi chcesz sprzedac caly browar.
PAK4 18 CZERWCA 2022 13:42
Rozumiem, że według ciebie, to informatyk jest synonimem informatora. ;-)
Swoją drogą, to powszechna szkoła, która ma dać podstawy poznania i zrozumienia świata, świadomego i krytycznego podejścia do rzeczywistości etc., NIE jest potrzebna elitom, które nami rządzą – ona jest dla nich wręcz szkodliwa. Ona jest potrzebna tylko dzieciom członków owych elit, które nami rządzą (Pareto się tu kłania). Powszechna wiedza powoduje bowiem, że zwyczajni ludzie zaczynają myśleć i wtedy buntują się przeciwko nierządom owych elit.
Różniczki i całki nigdy mi się zaś w praktyce nie przydały (poza zdawaniem egzaminów na studiach), podobnie jak filozofia, a tzw. studia genderowe to taka sama pseudonaukowa brednia jak np. astrologia czy egzorcystyka.
act 18 CZERWCA 2022 15:00
No, powiedzmy beczkę dobrego lagera.
No to pytam się matematyków, kiedy liczba staje się tak mała, że staje się ona praktycznie zerem? I kiedy liczba staje się tak wielka, że staje się ona praktycznie nieskończonością?
@kalvarya01
18 CZERWCA 2022
Nie ma żadnych problemów z dzieleniem przez 0, co tekst jasno podaje. Problemy takie mają jedynie laicy intuicjonistycznie postrzegający arytmetyke.
„Nie potrafimy dalej rozwiązać x*x = 2”.
Czyżby?
SQRT(2)*SQRT(2) = 2. Tak więc x=SQRT(2) Q.E.D.
act
18 CZERWCA 2022
Pytanie, czy dzieci są to w stanie pojąć.
mpn 18 CZERWCA 2022 15:17
Dzielenie przez zero daje nam zawsze nieskończenie wielką liczbę, czyli w praktyce absurdalny wynik, a czego nie mogą pojąc jedynie laicy błędnie postrzegający arytmetykę i całą matematykę jako naukę, a nie poprawnie, czyli jako rodzaj wiary zbliżonej w swej strukturze do religijnej. Stąd też w arytmetyce komputerowej mamy NaN (Not a Number) jako wynik dzielenia przez zero. „In computing, NaN is standing for Not a Number, is a member of a numeric data type that can be interpreted as a value that is undefined or unrepresentable” – NaN (ang. Not a Number czyli „nie liczba”) jest to element numerycznego typu danych, który może być interpretowany jako wartość niezdefiniowana lub nieprzedstawialna.
mpn 18 CZERWCA 2022 15:18
Zależy czyje dzieci i w jakim wieku.
Matka … jest tylko jedna … ! zawołał syn na widok ostatniej flaszki w lodówce … Tak sobie myślę prywatnie … jedyna na pocieszenie …
mpn, 15:18,
nie mam watpliwosci – rysunek/diagram, o ktorym pisze nie wymaga zadnej wiedzy o zbiorach nieskonczonych. Relacja 1 – 1 przedstawiona wizualnie przemowi do kazdego srednio rozgarnietego dziecka.
Potem oczywiscie nastapia trudne pytania.. I o to chodzi a nie o mechaniczne przeksztalcanie np. wielomianow, czy takiez obliczanie pochodnych juz na maturze.
„weźmy x * x = -1.”
Już w roku 1777 Euler wprowadził symbol ‘i’, który oznacza jednostkę urojoną wynoszącą pierwiastek z minus jeden czyli SQRT (-1). I tym właśnie jest ‘i’ – pierwiastkiem kwadratowymz minus jeden. A więc ponieważ i**2= -1, to i * i = -1, a więc x = i Q.E.D.
act 18 CZERWCA 2022 15:34
A ile jest nieskończność minus nieskończoność?
Zalezy od rodzaju nieskonczonosci moim zdaniem. Jesli jest to c= aleph- 1 rodzaj nieskonczonosci, to odejmujac jedna od drugiej powiedzialbym (z roznymi kwalifikacjami np. jakie elementy odejmujemy od jakich), to zero, null, zilch.
Tak mowi mi intuicja, nie studiowalem gleboko transfinites.
Po angielsku liczby niewymierne zwane są błędnie „irrational numbers”, czyli liczbami irracjonalnymi, gdy tymczasem są one jak najbardziej racjonalne, realne etc. Wzięło się to z wierzeń religijnych starożytnych Greków, konkretnie Pitagorejczyków, którzy zauważyli, że przekątna kwadratu o boku 1 jest niewspółmierna z jego bokiem, co właśnie oznacza niewymierność liczb, a oni przecież wierzyli, że Bogowie Olimpijscy stworzyli świat idealny, gdzie wszytko da się sprowadzić do prostych formuł matematycznych (w ich przypadku głównie geometrycznych). Błąd ten powtórzył nawet sam Kopernik, błędnie przyjmując, że planety muszą mieć idealne, czyli kołowe orbity.
act 18 CZERWCA 2022 15:47
Intuicja mówi nam, że Słońce krąży wokół płaskiej Ziemi i że jeśli Ziemia byłby kulista, to na antypodach ludzie musieli by chodzić do góry nogami. 😉
Intuicja mi mowi, ze zolw na ktorym stoi Ziemia stoi na innym zolwiu, ten na innym… i tak do samego konca.
act 18 CZERWCA 2022 15:44
Zakładasz, więc, że są skończone nieskończoności. Ale ten sam błąd popełnił nawet sam Cantor - idea tzw. najmniejszej liczby nieprzeliczalnej, czyli contradictio in adiecto („sprzeczność w przymiotniku”) – błąd logiczny polegający na zestawieniu dwóch wyrazów: określanego i określającego, które wzajemnie się wykluczają, np. kwadratowe koło, żonaty kawaler, czarna biel, głośna cisza itd. Określenie takie nie jest błędem logicznym tylko wtedy, jeżeli pełni ono funkcje poetyckie.
act 18 CZERWCA 2022 16:01
Mnie też! 🙂 Ale u mnie to są smoki.
act 18 CZERWCA 2022 15:44
A mnie zawsze nieskończoność wychodzi. Moze mój sofon się popsuł?
Cantor zwariowal, Goedel zaglodzil sie na smierc, Boltzmann popelnil samobojstwo – tego nie nalezy mowic aspirujacym matematykom 🙂
Są twórcy ( także ci przez duże TFU ) i wykonawcy.
Często jest tak, że owi „twórcy” mają „pomysł” ( genialny, zwariowany lub taki sobie ) lecz nie potrafią lub im się „nie chce” przerobić go w realny produkt.
Do tego potrzebny jest „wykonawca”, który sam na pomysł nie wpadnie ale jak mu sie powie CO ma zrobić to on to zrobi, bo wie JAK to się robi.
Każdemu z nich potrzebna jest inna wiedza i praktyka choć wskazane jest aby „twórca” także przeszedł „staż praktyczny” – wtedy jego projekty stają się „wykonalne”.
kaesjot,
np. ‚praktyka budowlana’ po pierwszym roku architektury: dwa tygodnie stania po pachy w blocie w upale i kopanie rowow pod okiem sadysty majstra. 🙂
act 18 CZERWCA 2022 16:33
Raczej należy mówić! Także o tym, że Galois umarł młodo w niepotrzebnym pojedynku, Turing popełnił samobójstwo z powodu swego zboczenia płciowego, Markow umarł młodo na gruźlicę etc.
kaesjot 18 CZERWCA 2022 16:37
Ci „twórcy” brzydzą się często pracą.
act 18 CZERWCA 2022 16:51
Bzdura. Praktyka w biurze budowy, przy poprawianiu planów, wykonywaniu kosztorysów etc. Pamiętam dobrze moje studenckie praktyki w FSO czy Rafinerii Płockiej. Jeśli byli tam jacyś sadyści, to trzymali się ode mnie z daleka.
To, co zrobiono z Turingiem wola o ‚pomste do nieba’. Niebotyczna hipokryzja i okrucienstwo.
kalvarya01 16:51,
mowie ‚z pierwszej reki’.. ale niewazne.
k. 16:58…
kalvarya01
18 CZERWCA 2022
Bzdura, dzielenie przez 0 nic nie daje, bo dać nie może. Wynika to jednoznacznie z aksjomatów Peano.
Na temat matematyki się nie wypowiem.
Natomiast na temat matematyków, warto.
Bez matematyki nie ma konstrukcji, przemysłu, postępu technicznego, wynalazków, badań biologicznych, chemii, wielu innych dziedzin PRAKTYCZNYCH.
Dar matematyczny jest zjawiskiem skrajnie rzadkim.
Talenty sa rozchwytywane.
Pytanie brzmi.
KTO najwięcej za nie płaci?
I to moim zdaniem zaczyna stanowić problem.
Najwięcej płaci za talent sektor finansowy, nie produkujacy niczego poza algorytmami umozliwiającymi ogranie „kasyna”.
Te talenty wykorzystane w rozwiazywanie REALNYCH problemów technicznych, światowych, byłyby zdecydowanie efektywniejsze, choć gorzej opłacane.
Potentatami w matematyce jest jedynie kilka krajów inwestujących w naukę na poziomie podstawowym.
Zgadnijcie, które….
Przeciwko … 13 i w piątek … Tak sobie myślę prywatnie … komu na tym zależy …
Rozbawiło mnie kilka artykułów w UNZ, które dowodziły, że matematyka jest RASISTOWSKA, trzeba wyrównać szanse….
W tym ujeciu, szanse talentów matematycznych, są ZEROWE….
act 18 CZERWCA 2022 17:00
On był sam sobie winien, że nie chciał się leczyć…
kalvarya01
18 CZERWCA 2022
18:30
Elektrowstrząsy nie sa leczeniem, są WARUNKOWANIEM.
A takie metody stosowano w tamtych czasach.
Powtórzę.
To nie choroba, to genetyczna dysfunkcja.
Nawet obecnie niepodatna na korekcję znanymi metodami.
Pryzpomina mi się jakeś stare opowiadanko, o umieszczeniu ludzi w polu elektromanetycznym o określonej częstotliwosci.
Wzmacnialo to talent matematyczny, rujnując jednocześnie zdrowie osobników w nim umieszczonych.
Ciekawe, jak osobniki umieszczane obecnie w takim polu wytwarzanym przez współczesne media będą reagowały?
5G, 6G…
Populacje testowe są liczne.
Uprzedzenie do 13 pachnie homofobią … Tak sobie myślę prywatnie … nie jest naukowe …
Czytałem kiedyś o przeprowadzonej przez władze chińskie akcji akcji wynajdywania dzieci wybitnie zdolnych. Znaleziono ich ok. 200 tys. Nie pisano, co z nimi zrobiono ale znając chiński pragmatyzm można się domyślać, że otoczono je specjalną opieką – odrębne szkoły, internaty, odpowiednie, dostosowane do talentu programy nauczanie, studia w najlepszych uczelniach, staże w czołowych, innowacyjnych firmach a w przyszłości praca w OBR-ach.
I to oni będą motorem napędowym chińskiej gospodarki.
Przyjmując założenie , że wskaźnik udziału tych wybitnie zdolnych dzieci u nas jest zbliżony do chińskiego to powinno ich być u nas ok. 5 tys. czyli 130 na 1 mln mieszkańców. Oznacza to od jednej ( woj. opolskie) do 5-6 ( W-wa + woj. mazowieckie ) specjalnych zespołów szkół ( SP +średnia ukierunkowana ) .
Szczegółowe rozwiązania dostosować do potrzeb i możliwości.
Trzeba tylko chcieć !!!
Problem w tym, że rządzący w Polsce po 1989 roku tego NIE CHCĄ CHCIEĆ i na siłę chcą stworzyć hybrydę – pingwino -orło-strusia zamiast rozwijać każdego osobno, z maksymalnym wykorzystaniem jego zdolnosci.
mpn 18 CZERWCA 2022 17:24
Opierasz sie na arbitralnie przyjętych i nieweryfikowalnych aksjomatach, tak jak ksiądz. A teraz usiądź i pomyśl:
½ = 1/2**1 = 0.5
¼= 1/2**2 = 0.25
1/16 = 1/2**4 = 0.0625
1/256 = 1/2**8 =0.00390625
…
1/274 877 906 944 = 1/2**38 = 3.63797880709171295166015625e-12, przy czym 2**38 to jest szacowana liczba gwiazd w Drodze Mlecznej (ok. 400 mld)
…
1/302 231 454 903 657 293 676 544= 1/2**78 = 3.3087224502121106994856347682799e-24, przy czym 2**78 jest to szacowana liczba gwiazd we Wszechświecie (3*10**23), niewiele mniejsza niż Liczba Avogadro (6,023*10**23) – Liczba Avogadra jest wielkością stałą informującą o liczbie cząsteczek lub atomów zawartych w jednym molu (jednostce liczności materii) substancji, przy czym jeden mol jest taką liczbą atomów jaka jest zawarta w 12 gramach izotopu węgla 12C
…
1/158 456 325 028 528 675 187 087 900 672 = 1/2**97 = 6.3108872417680944432938285223419e-29, przy czym 2**97 jest to teoretyczny czas rozpadu protonu w latach (2,1*10**29)
…
1/463 168 356 949 264 781 694 283 940 034 751 631 413 079 938 662 562 256 157 830 336 031 652 518 559 744 = 1/2**258 =2.1590421387736111563465879657001e-32
…
1/926 336 713 898 529 563 388 567 880 069 503 262 826 159 877 325 124 512 315 660 672 063 305 037 119 488 = 1/2**259 = 1.0795210693868055781732939828501e-32, przy czym 2**259 jest to ilość atomów w obserwowalnym Wszechświecie (ok. 10**78)
Większe liczby niż 10**78 nie mają więc sensu, podobnie jak liczby mniejsze niż około 1.08e-32, ale jakże daleko jest tej pierwszej do nieskończoności, a tej drugiej do zera… I jak je zapisać jeszcze większe liczby w pamięci komputera?
O swiatowym prymacie nie rozstrzygną godziny poświęcone religii, socjologii, gender, filozofii.
Tylko godziny poswęcone matematyce, biologii, fizyki, chemii.
Inzynierowie, nie kapłani.
wiesiek59 18 CZERWCA 2022 18:37
Jeśli homoseksualizm nie jest chorobą a „genetyczną dysfunkcją”, to rację ma Putin nazywając wojnę na Ukrainie „wojskową operacją specjalną”. Recesja nie jest też recesją a dekoniunkturą, inflacja – nadmiarem podaży pieniądza, bezrobocie – niepełnym zatrudnieniem a policja – anielicją. 😉
On most computer architectures, the space allocated for any integer is four bytes. Four bytes is equivalent to 32 bits which can represent an integer no larger than 2**31-1 (about 2 billion). If the integer is signed, then the largest number that can be arithmetically manipulated at one time is 2**30-1 (about 1 billion). Many architectures, however, will also support manipulation of 64 bit integers if the programmer explicitly asks for the space. Still, this is quite a limitation considering the context of RSA encryption. Decrypting a typical message may involve something like 200**150 mod 400 . It would not be possible to compute 200**150 on any desktop machine because this is approximately; much bigger than any integer that can fit in a computer’s register where it can be manipulated.
Decrypting a message is possible because it also uses modular arithmetic. There is no way to compute 200**150 with the standard architecture, but because there is modular arithmetic involved, there is a way to keep the numbers small at each step of the computation, never allowing them to exceed 2**32 (or for certain, 2**64). The algorithm to do so is as follows: Factor the desired number into powers so that each factor can be easily computed from the previous factor. To compute each factor, we square the previous factor and then reduce modulo n.
Decrypting a message is possible because it also uses modular arithmetic. There is no way to compute with the standard architecture, but because there is modular arithmetic involved, there is a way to keep the numbers small at each step of the computation, never allowing them to exceed (or for certain, ). The algorithm to do so is as follows: Factor the desired number into powers so that each factor can be easily computed from the previous factor. To compute each factor, we square the previous factor and then reduce modulo n.
https://www.math.arizona.edu/~ura-reports/021/Singleton.Travis/resources/bignums.htm
P.S. 200**150 mod 400 means it is the remainder when you divide 200**150 by 400.
Enough mathematics! It causues head aches!
wiesiek59 18 CZERWCA 2022 18:25
Matematyka jest abstrakcyjna i po uwzględnieniu natury aksjomatów często jest ona całkiem logiczna, a więc rzadko która kobieta jest w stanie ją zrozumieć…
wiesiek59 18 CZERWCA 2022 18:20
Bez „wyższej” matematyki możliwe są konstrukcje, przemysł, postęp techniczny, wynalazki, badania biologiczne, chemiczne i wszystkie niemal dziedziny PRAKTYCZNE, które wymagają tylko opanowania podstaw arytmetyki i geometrii. Np. cała teoria mnogości nie jest nikomu w praktyce potrzebna, gdyż nasz Wszechświat jest przecież skończony w czasie i przestrzeni.
Zgda, prawdziwy dar matematyczny jest zjawiskiem skrajnie rzadkim, ale talenty matematyczne wcale nie są rozchwytywane, gdyż w praktyce liczą się umiejętności praktyczne a nie abstrakcyjne matematyczne myślenie oparte na nieweryfikowalnych założeniach. Sektor finansowy opanowany jest zaś przez głupków, którzy myślą, z metodami matematycznymi „przechytrzą” rynek, szczególnie finansowy, który jest jednak system tak złożonym i tak chaotycznym, że żaden model matematyczny nie jest i nigdy nie będzie go w stanie opisać, chyba że ktoś wynajdzie zupełnie inną matematykę, nie opartą na żadnych apriorycznych a nieweryfikowalnych założeniach. Pamiętam doskonale, jak matematycy, zatrudnieni w towarzystwie ubezpieczeniowym, gdzie pracowałem jako informatyk (programista), dorowadzili to towarzystwo do bankructwa, gdyż ich model źle oszacował trendy na giełdzie i kupili oni i to na dodatek na kredyt, nie te akcje, które powinni kupić. A trzeba wiedzieć, że towarzystwa ubezpieczeniowe najwięcej zarabiają grając na giełdzie, czyli w kasynie, pieniędzmi otrzymanymi od osób, które się w nich, w swej naiwności, ubezpieczyły, najlepiej na życie.
Natomiast rozwiazywanie REALNYCH problemów technicznych a szczególnie społecznych leży poza domeną matematyki, jako iż większość tych problemów nie da się „zdigitalizować”, czyli opisać w postaci liczbowej.
Data zgonu jedną z liczb rzeczywistych … Tak sobie myślę prywatnie … na jej podanie nie ma mocnych … z przyczyn naturalnych … oczywiście …
Kto dzisiaj uczy całek w szkołach?
MATURA 1950
Drwal ściął drzewo za 100 złotych,
5 % odpala.
Drugie tyle – koszt roboty.
Oblicz dochód drwala.
MATURA 1980
Drwal ściął drzewo za 100 złotych,
Na pniu sprzedał całość.
Przepił dychę do soboty.
Ile mu zostało?
MATURA 2000
Drwal ściął drzewo za 100 złotych,
Dychę wziął pan Czesio.
Koszt odejmij od tej kwoty.
Zaznacz: dziewięćdziesiąt.
MATURA PO REFORMIE
Z tym zadaniem ma kłopoty
Niejeden mądrala:
Drwal ściął drzewo za 100 złotych.
Pokoloruj drwala.
Przypomnijmy:
List otwarty rosyjskich naukowców i dziennikarzy naukowych przeciwko wojnie z Ukrainą
My, rosyjscy naukowcy i dziennikarze naukowi, wyrażamy stanowczy protest przeciwko działaniom militarnym sił zbrojnych naszego kraju na terytorium Ukrainy. Ten fatalny krok prowadzi do ogromnych ofiar w ludziach i podważa fundamenty ustalonego międzynarodowego systemu bezpieczeństwa. Odpowiedzialność za rozpoczęcie nowej wojny w Europie spoczywa wyłącznie na Rosji. Ta wojna nie ma żadnego sensownego usprawiedliwienia. Próby wykorzystania sytuacji na Donbasie jako pretekstu do rozpoczęcia operacji wojskowej nie są wiarygodne. To dość oczywiste, że Ukraina nie stanowi zagrożenia dla bezpieczeństwa naszego kraju. Wojna przeciwko niej jest niesprawiedliwa i w sposób oczywisty bezsensowna. Ukraina była i pozostaje bliskim nam krajem. Wielu z nas ma na Ukrainie krewnych, przyjaciół i współpracowników naukowych. Nasi ojcowie, dziadkowie i pradziadkowie wspólnie walczyli przeciwko nazizmowi. Rozpętanie wojny w imię ambicji geopolitycznych przywódców rosyjskich, napędzane wątpliwymi fantazjami historiozoficznymi, jest cyniczną zdradą ich pamięci.
Szanujemy państwowość ukraińską, która opiera się na realnie funkcjonujących instytucjach demokratycznych. Rozumiemy europejski wybór naszych sąsiadów. Jesteśmy przekonani, że wszystkie problemy w stosunkach między naszymi krajami można rozwiązać pokojowo. Po rozpoczęciu wojny Rosja skazała siebie na międzynarodową izolację, na pozycję kraju wyrzutka. Oznacza to, że my, naukowcy, nie będziemy teraz mogli właściwie wykonywać swojej pracy: w końcu prowadzenie badań jest nie do pomyślenia bez pełnej współpracy z kolegami z innych krajów. Izolacja Rosji od świata oznacza dalszą degradację kulturową i technologiczną przy całkowitym braku pozytywnych perspektyw. Wojna z Ukrainą to krok donikąd.
Z goryczą zdajemy sobie sprawę, że nasz kraj, który w decydujący sposób przyczynił się do zwycięstwa nad nazizmem, stał się inicjatorem nowej wojny na kontynencie europejskim. Żądamy natychmiastowego zaprzestania wszelkich działań wojennych przeciwko Ukrainie. Domagamy się poszanowania suwerenności i integralności terytorialnej państwa ukraińskiego. Żądamy pokoju dla naszych krajów.
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Domyślam sie, ze naukowcy rosyjscy, po uplywie 100 dni wojny, stracili koncept.
@MARKOT
Stare…
uaktulniona wersja
… udowodnij ze drwal jest katolikiem i patriota
u nas (USA) aby uczen szkoly licealnej mogl dostac sie do szkoly medycznej
musi miec zaliczony calculus oraz chemie organiczna.
Dla wielu jest to bariera nie do przebycia.
@R.S.
Stare? Wiem, ale ja już tylko stare pamiętam 🙁
Take it with a grin of salt 😉
Wzór na powierzchnię całkowitą kuli: pole podstawy dodać pole powierzchni bocznej.
Trójkąt to kwadrat o trzech kątach.
act 18 CZERWCA 2022 15:44 napisał: Zależy od rodzaju nieskończoności moim zdaniem. Jesli jest to c= aleph- 1 rodzaj nieskończoności, to odejmując jedna od drugiej powiedziałbym (z rożnymi kwalifikacjami np. jakie elementy odejmujemy od jakich), to zero, null, zilch.
- A słyszałeś o Hotelu Hilberta? W skrócie jest to paradoks opisany przez Davida Hilberta w celu ilustracji trudności w intuicyjnym rozumieniu pojęcia „ilości” elementów zbioru z nieskończoną liczbą elementów. Wyobraźmy sobie, że jesteśmy recepcjonistą w hotelu, w którym jest nieskończona liczba pokoi. Wszystkie pokoje są już zajęte, gdy przychodzi do nas kolejny klient chcący wynająć pokój. Wydawałoby się, że sytuacja jest bez wyjścia i musimy klienta „odprawić z kwitkiem”, ale na szczęście nasz hotel ma nieskończoną liczbę pokoi, więc możemy klienta z pokoju numer 1 przekwaterować do pokoju nr 2, tego z pokoju nr 2 do pokoju nr 3, itd. Ogólnie można powiedzieć, że dokonujemy przekwaterowania klientów z pokojów o numerze ‘n’ do pokojów o numerze ‘n+1’. W ten sposób wszyscy nasi wcześniejsi klienci mają gdzie mieszkać, a my mamy wolny pokój nr 1, do którego możemy zakwaterować naszego nowego gościa. Tak więc, mimo że hotel był pełny, znalazło się w nim miejsce dla nowego klienta.
Mówiąc zaś prościej – jeśli mamy nieskończoną ilość pokojów do dyspozycji, to pomieścimy w nim nieskończoną ilość wycieczek z nieskończoną ilością osób. I wcale nie musimy robić tych tricków zaproponowanych przez Hilberta, gdyż jeśli mamy nieskończoną ilość pokojów do dyspozycji, do nigdy nie wyczerpiemy ich zasobu. A jeśli nieskończoność + nieskończoność = nieskończoność, to także nieskończoność – nieskończoność = nieskończoność, gdyż mając nieograniczony zasób pokojów, to możemy nieskończoną ilość razy odejmować od niego nieskończoną ilość pokojów, wciąż mając do dyspozycji ich nieskończoną ilość.
Jedyny realny problem jest tu zaś taki, że nieskończoności w naturze nie ma, gdyż nasz Wszechświat jest skończony zarówno w czasie jak i w przestrzeni i co do tego, to zgadzają się wszyscy poważni fizycy, astronomowie, kosmologowie etc., gdyż istnieją na to naukowe, czyli empiryczne dowody, np. na jego rozszerzanie się, a przecież nieskończenie wielki Wszechświat, zajmując z definicji „wszystko”, nie mógł by się przecież powiększać gdyż byłby on nieskończenie wielki. Innymi słowy -rozważania o nieskończoności prostu NIE mają sensu, chyba, że służą one do ilustracji krytyki tzw. „chłopskiego” czy też „zdrowego” rozumu („common sense”), który mówi nam że płaska Ziemia krąży dookoła okrągłego Słońca, że na antypodach ludzie chodzą do góry nogami i że dając księdzu „co łaska”, kupujemy sobie odpuszczenie grzechów i tym samym miejsce w raju…
I na koniec – każdy zbiór z nieskończoną ilością elementów jest z definicji nieprzeliczalny, gdyż nigdy nie ma on i to z definicji ostatniego elementu. Definicja zbioru nieskończonego jest bowiem taka, że jest to zbiór niewyczerpalny, zbiór w którym nie ma ostatniego elementu, gdyż jeśli „dojdziemy” do elementu numer ‘n’, to zawsze jest w nim element numer ‘n+1’ i to niezależnie od tego, jak wielką liczbą jest ‘n’. Jeśli więc mamy plik banknotów z ich nieskończoną ilością, to nigdy, nawet dysponując nieskończoną ilością czasu (a co, jak wiadomo jest zresztą niemozliwe, gdyż nie żyjemy wiecznie a nasz Wszechświat jest przecież skończony także i w czasie) nie „dojdziemy” do ostatniego banknotu, gdyż w naszym pliku znajduje się nieskończona ich ilość, a więc choć mamy pierwszy banknot, to mając ich nieskończoną ilość, nigdy nie możemy „dojść” do ostatniego banknotu. Pomijam tu już problem praktyczny, czyli że taki nieskończenie wielki plik banknotów musiałby zajmować nieskończenie wielką przestrzeń, a więc nic poza nim nie mogło by istnieć, w tym i jego właściciel. A to jest kolejny paradoks nieskończoności. Nic więc dziwnego, że Cantor zwariował…
Teraz kolej na list israelskich naukowców przeciwko pacyfikowaniu sąsiadów … Tak sobie myślę prywatnie … Holokaust-bis sąsiadów jest grzechem … pod pretekstem przestrzeni życiowej …
R.S. 19 CZERWCA 2022 0:27
I dobrze. W Polsce egzaminy na studia medycynę są zbyt łatwe, a więc później mamy takich lekarzy, jakich mamy… A calculus to jest po naszemu rachunek różniczkowy i całkowy czyli europejska matematyka z XVII wieku. Ciekawe, czy na tym egzaminie wymagają umiejętności rozwiązywania równań różniczkowych? Ja bym tam dodał jeszcze geometrię różniczkową i mechanikę kwantową. 😉
Orteq 18 CZERWCA 2022 23:52
NIE na temat i bzdura. Odpowiedzialność za rozpoczęcie nowej wojny na wschodzie Europy spoczywa przecież praktycznie wyłącznie na Zachodzie, w tym głównie na USA, które to państwo dąży do włączenia Ukrainy do NATO i tym samym do utworzenia swoich kolejnych baz wojskowych tuż przy granicy z Rosją. To jest wojna o światową hegemonię, a nie tylko o Ukrainę. Państwowość ukraińską NIE opiera się zaś na realnie funkcjonujących instytucjach demokratycznych, a tylko na korupcji, fałszowaniu historii, dyskryminacji mniejszości etnicznych i językowych oraz last but not least na kulcie faszyzmu (S. Bandera, UPA, OUN, ukraińska dywizja Waffen SS etc.).
SŁOWIANIN STANISŁAW 19 CZERWCA 2022 6:36
Taki list to mogli by oni wysłać chyba tylko ze Szwajcarii czy innego Monako, ale NIE z Izraela…
mpn 18 CZERWCA 2022 17:24 Napisał: „Bzdura, dzielenie przez 0 nic nie daje, bo dać nie może. Wynika to jednoznacznie z aksjomatów Peano.”
Już odpowiedziałem (kalvarya01 18 CZERWCA 2022 19:25) ale jeszcze tylko trochę o aksjomatach Peano. Otóż niektórzy matematycy zaliczają zero do liczb naturalnych a inni nie. I NIE jest to wyłącznie kwestia nazewnictwa, gdyż liczba zero ma zupełnie inne właściwości niż liczba jeden, np. nie ma problemów z dzieleniem przez jeden, ale są i to poważne problemy wynikające z każdej próby dzielenia przez zero. Jak więc widać, wszystkie liczby naturalne maja takie same właściwości, ale istnieje liczba, konkretnie zero, która ma zupełnie inne właściwości niż wszystkie pozostałe liczby. Zauważ też, że aksjomatyka Peano NIE zawiera definicji dzielenia.
Banderowcy żałują wyzwolenia przez Armię Czerwoną … pod niemiecką okupacją to oni rządzili na Wołyniu … Tak sobie myślę prywatnie …. sprzedajni są politycy w ramach rusofobii …
Skandal. Biden prześladuje gejów!
Jak donosi Associated Press, prezydent USA Joe Biden upadł, kiedy próbował zsiąść z roweru pod koniec sobotniej przejażdżki w pobliżu swojej wakacyjnej posiadłości w Delaware. Do przywódcy USA od razu podbiegli agenci Secret Service, którzy otoczyli prezydenta i pomogli mu stanąć na nogi.
Biden miał powiedzieć otaczającym go dziennikarzom, że miał problemy ze zdjęciem butów z PEDAŁÓW, gdy próbował się zatrzymać. Prezydent USA chciał przystanąć, by porozmawiać ze stojącymi przy drodze ludźmi.
https://wiadomosci.gazeta.pl/wiadomosci/7,114881,28596139,usa-wypadek-joe-bidena-podczas-wycieczki-rowerowej-prezydent.html#s=BoxOpImg8
Komentarz:
lechpierwszy „Gdzie protesty grup LGBTQI+?!? Oto prezydent mocarstwa swiatowego Bajden „miał problemy ze zdjęciem butów z pedałów” inic? Taka dyskryminacja, niewolnictwo wlasciwie i nic? Jeszcze niedawno tak slodko sie o nich wypowiadal, a tu taki afront? Gdzie teczowe protesty, pytam? No gdzie?”
SŁOWIANIN STANISŁAW 19 CZERWCA 2022 7:16
Od roku 1989 rządzą nami PPA – Płatne Pachołki Ameryki.
kalvarya01 6:35,
A i owszem znam: Hilbert’s Hotel, Mary’s Room, Leibniz’ Mill i wiele
innych paradoksow, alegorii, ‚thought experiments’ zwiazanych z matematyka, qualiami, swiadomoscia, epistemologia, logika etc.
A propos nieskonczonosci: w matematyce mozna m. in. byc Intuicjonista, Konstruktywista, czy np. Formalista jak sam Hilbert. It’s all fun and games!
Bez wielkosci nieskonczenie malych natomiast caly calculus trzeba by budowac ‚from scratch’!
Leibniz’s Mill..
Dzięki wyzwoleniu kraju nad Wisłą przez Armią Czerwoną Szaleni naukowcy mają możliwość prezentowania swoich poglądów … Tak sobie myślę prywatnie … w GG takich możliwości zapewne nie byłoby … o czym przypomina Kaczyński … wrażliwy na germanizację …
kalvarya01 – 6:53
„Orteq 18 CZERWCA 2022 23:52 –
NIE na temat i bzdura. Odpowiedzialność za rozpoczęcie nowej wojny na wschodzie Europy spoczywa przecież praktycznie wyłącznie na Zachodzie, w tym głównie na USA”
Jak może byc ‚nie na temat’, jeśli ogólnym tematem jest ‚szaloność naukowców’ ? Dowodzisz tego już sam, w reszcie swojej oświeconości unaukawionej.
Natomiast z bzdura zgoda. Szczególnie w odniesieniu do Twojej oświeconości.
Bez wylewnego podziwu
https://www.picuki.com/media/2860517274897506743
SŁOWIANIN STANISŁAW 19 czerwca 2022 9:30
Dodam więcej – posiedli by jedynie umiejętność podpisania się i liczenia w zakresie do 100. Mogliby zatem dyskutować jedynie o pasaniu bydła i machaniu łopatą ewentualnie dyskutować, czy do podcierania tyłka lepsza świeża trawa czy suche siano albo liść łopianu. Do tego jeszcze, co mozna zrobić, aby dynia ( po naszymu korbol) wyrosła naprawdę olbrzymia.
@kalvarya01:
> Różniczki i całki nigdy mi się zaś w praktyce nie przydały
A mi owszem. Często i gęsto. Oczywiście, z uwagą, że w informatyce, przestrzeń i czas są praktycznie skwantowane 🙂
> Państwowość […] NIE opiera się zaś na realnie funkcjonujących instytucjach demokratycznych, a tylko na korupcji, fałszowaniu historii, dyskryminacji mniejszości etnicznych i językowych oraz last but not least na kulcie faszyzmu
Pięknie podsumowałeś rządy PiS. Serio. Ja bym lepiej tego nie zrobił.
Nawet Watykan nie jest absolutną demokracją … Tak sobie myślę prywatnie … dlaczego państwo Watykan omijają sankcje tzw. zachodniej cywilizacji …. już za sam fakt wykluczenia kobiet ze stolca …
Zastanowić się należy, kto za kilka lat będzie nauczał matematyki.
Skoro kasjerka w Biedronce zarabia 2X więcej niż początkujący nauczyciel..
@kalvarya01
19 CZERWCA 2022
W Polsce od lat nie ma egzaminów na studia. Naprawdę wypadałoby mieć przynajmniej elementarne pojęcie, o czym się pisze.
@wiesiek59
W czasach PRL-u kasjerki po Zasadniczej Szkole Handlowej potrafiły liczyć „w pamięci ” szybciej niż profesorowie matematyki. Kasy były tylko zwykłymi sumatorami więc musiała zidentyfikować towar ( dzisiaj załatwia to w 90% skaner kodu kreskowego ) znać cenę jednostkową i pomnożyć ją w pamięci przez ilość i wtedy wynik wbijała do kasy, Dodatkowo musiała obliczyć „resztę” do wydania.
Dzisiaj wystarczy , że umie WYDAĆ RESZTĘ bo jej wielkość też kasa sama wylicza po wbiciu wpłaconej kwoty. A i to tylko w przypadku, gdy klient płaci gotówką a to coraz rzadziej ma miejsce.
Czy do tego potrzeba ukończyć studia ?
Jak wytłumaczyć zamieszkiwanie Donbasu i okolic przez Rosjan … Tak sobie myślę prywatnie … ich sytuacja przypominała rezerwaty u jankesów dla rdzennej ludności … ktoś ruszył w celu ich uwolnienia … Ukrainiec to pojęcie administracyjne … nie ma korzeni historycznych … jak pisowiec …
Gwoli ścisłości, to na medycynę i prawo można startować dopiero po bakałarzu.
Potrzeba mieć tez wysoki wynik w MCAT a do szkoły prawniczej LSAT. To takie testy bardzo ostre sprawdzające wiedzę.
Czy obywatel Watykanu to narodowość … Tak sobie myślę prywatnie … Rusini to już powód do dumy … z Kijowem w herbie …
kaesjot
19 CZERWCA 2022
11:52
Matematyka, chemia, fizyka, ćwiczą pamięć, logikę, umiejętność wnioskowania, kojarzenia.
A to przydaje się na późniejszym etapie życia.
Nawet nudne wkuwanie aksjomatów, definicji, wzorów, służy rozwojowi kory mózgowej.
Jestem za daleko od obecnego systemu nauczania, by wnioskować, jakie będą skutki tych wszelkich dotychczas przeprowadzonych reform, polegających na obcięciu ilosci godzin przedmiotów ścisłych i okrojeniu materiału.
Nie mówiąc już o realnym cięciu płac nauczycieli, wpływających bezpośrednio na ich jakość.
Wyborca ma wiedzieć gdzie postawić krzyżyk … Tak sobie myślę prywatnie … o likwidacji ciemności nad urną …
wiesiek59 19 czerwca 2022 12:48
Mam kolegę – kilka lat starszego ode mnie. Po 7-mej klasie SP poszedł w „naukę zawodu” , zaliczył zawodówkę a potem wieczorowo zrobił technikum i maturę. Lubił popisywać się dobrą pamięcią cytując różne definicje, twierdzenia i wzory .
Na moje pytanie czy rozumie co to znaczy , do czego służy i jak to zastosować w praktyce odpowiadał, że nie. To po cholerę tobie ta wiedza ? – pytam się go.
Wielokrotnie przytaczałem przykłady absolwentów politechniki, którzy nie znali a jeśli nawet znali to nie potrafili w praktyce zastosować zasad maszyn prostych – dźwigni jedno – lub dwustronnej , równi pochyłej i związanymi z nią klinami i śrubami itp. Sam byłem świadkiem, jak student politechniki przyszedł do sklepu metalowego ŻĄDAJĄC by mu pokazano, jak wygląda śruba. Dobrze, że wiedział do jakiego sklepu się udać.
To jest zwyczajne „rzucanie pereł przed wieprze”!
@Markot
Ja już tylko stare pamiętam
… obsmialem się
Ja bym jeszcze dodał, ze kiedyś miałem więcej cierpliwości i tolerancji do bzdur.
Powracając do liczb rzeczywistych.
W dzisiejszych czasach gdy chcemy narysować okrąg, prawdopodobnie robimy to za pomocą komputera i punkty znajdujemy z rozwiązania równania
X^2 + Y^2 = R^2
Mając to na uwadze można zacząć perorować na temat bitowości, fixed point calculations, kwantyzacji w procesorach, propagacji i kumulacji błędów w obliczeniach, itd.
Wkrótce po tym oznajmić światu, ze liczby rzeczywiste nie istnieją no, bo jak.
A starzy ludzie tak jak tu piszący R.S., Markot i nieliczna grupka innych, pamięta takie urządzenie co się nazywało cyrkiel.
I tak to proste urządzenie znane od czasów starożytności, jest w stanie wyrysować w sposób ciągły bez kwantyzacji zbiór punktów rzeczywistych na płaszczyźnie, których to odległość od ustalonego punktu (zwanego środkiem okręgu), jest równa zadanej odległości (zwanej promieniem okręgu).
W pierwszej klasie liceum, poznawaliśmy geometrie z użyciem cyrkla i linijki, nauka ta została na cale życie.
Jeśli chodzi o śruby to spirale Archimedesa i inne heliksy tez konstruowaliśmy.
Prośba o pokazanie śruby wcale nie jest pozbawiona sensu…
może byc prawoskrętna, lewoskrętna, metryczna, calowa, ocynkowana, stalowa, z głowicą pod klucz hexagonalny, torx, mająca nacięcie phillipsowskie, itd.
kaesjot
19 CZERWCA 2022
13:39
Sądzę że nasze pokolenie jest ostatnim, które posługiwało się narzędziami.
Potrafiło skonstruować szałas, wbić prosto gwóźdź, wymienić gniazdko, itp. banalne czynnosci codziennego zycia, bez pomocy fachowców.
Obecne pokolenie poza perfekcyjnym posługiwaniem się dwoma kciukami, zaczyna być bezradne wobec prozy życia.
Zdolności manualne zanikaja, wraz z brakiem skojarzeń wynikających z braku obserwacji innych przy pracy.
Niedawno pomogłem pewnej wysoce kształconej jednostce wymienić dętkę w rowerze.
Ani nie wiedziała jak, ani że coś takiego istnieje…
Dlatego jestem bardzo sceptyczny wobec perspektyw wasko wyspecjalizowanej, białej cywilizacji.
Szcególnie patrząc na wyczyny rzadzacej obecnie klasy politycznej.
Nie jest w stanie powiązać przyczyn ze skutkami swych decyzji.
Ich tzw. „eksperci” mają podobną wadę.
Są teoretykami ze stopniami naukowymi, nie parającymi się w zyciu żadną pracą.
Szczelnie odizolowanymi od plebsu i jego problemów.
Cyrkiel, pion, sznurek, trzy paliki….
To wystarcz do wybudowania większości konstrukcji.
Reszta to doświadczenie i znajomość materiału który jest dostępny, jego własciwości.
Niektóre systemy irygacyjne, akwedukty, mosty, budowle, dalej stoją.
wiesiek59 19 CZERWCA 2022 14:29
Otóż to!
wiesiek59 19 CZERWCA 2022 14:24
Coś bardzo podobnego chciałem właśnie napisać…
Drodzy Panowie, drogie Panie,
ale czy Państwo w tych zachwytach, że kiedyś to było i że potrafią coś, czego młodzi nie potrafią, zadają sobie pytanie odwrotne — czy młodzi może potrafią coś, czego starsze pokolenie nie kuma?
PS.
Z gwoździem prosto to różnie. Ursusem C-330 uczyłem się dopiero w ub. roku jeździć. Szałasu w życiu nie budowałem. Gniazdko — oczywiście, bez problemu; w ogóle elektryka na plus, nawet jeśli moje luty były najbrzydsze na świecie. Swoją drogą, a propos uzdolnień manualnych, to ktoś ćwiczył copperplate? Bo całkiem nieźle idzie minuskuła karolińska, czy gotyk, ale copperplate nie na moje ręce, młodego i niewyrobionego manualnie pokolenia. Dętka w rowerze… no trochę się z nią męczę, wolę gdy młodzi to robią — ci młodzicy w warsztatach rowerowych są dużo sprawniejsi niż ja.
R.S. 19 czerwca 2022 14:09
„Prośba o pokazanie śruby wcale nie jest pozbawiona sensu…
może byc prawoskrętna, lewoskrętna, metryczna, calowa, ocynkowana, stalowa, z głowicą pod klucz hexagonalny, torx, mająca nacięcie phillipsowskie, itd.”
Czy ta wiedza szczegółowa na temat rodzajów śrub potrzebna jest komuś kto nie łapie ogólnej zasady działania i stosowania śrub ?
Najlepszą definicję śruby usłyszałem od sprzedawcy ( mniej więcej w moim wieku ) na stoisku elementów złącznych w ( innym ) sklepie metalowym. Wg niego śruba to równia pochyła nawinięta na walec. Oczywiście najlepsza tylko dla tych co pojmują zasadę równi pochyłej.
@wiesiek59 – mój pradziadek, stelmach z zawodu przy wyznaczaniu kąta prostego stosował zasadę 3-4-5 pojęcia nie mając że jest ona pochodną prawa Pitagorasa.
Do wyznaczania poziomu stosował wypełniony wodą wąż gumowy ze szklanymi rurkami na końcach choć nie wiedział, iż działa to na zasadzie naczyń połączonych.
@PAK4
Ursus model C 330 zaczęto produkować w 1967 a zaniechano jej 20 lat później czyli nie są produkowane od 25 lat a nadal wielu rolników je stosuje.
Oznacza to, że były to bardzo dobre , niezawodne i trwałe traktory. Zdarza się jeszcze zobaczyć pracujące Ursusy C4011 , którego produkcję zakończona w 1970 a więc ponad 50-letnie.
To chyba nie kiepska jakość produkowanych traktorów sprawiła, że Zakłady Ursus rozp…..no ?
Zatem co ?
@PAK
ale tabliczkę mnożenia to chyba warto znać?
Z innymi urządzeniami np. silnikiem samochodowym to mogę sobie tylko na niego popatrzeć.
Świecy samemu już się nie da zmienić.
I szczerze mówiąc mam to w nosie.
Ale do komputera nikomu nie dam się dotknąć i co z tego?
Gdy chodzi o IPhone i gesty operacyjne to znam tylko trzy może cztery,
wiec osoba mloda potraktuje mnie jako analfabetę iPhoniczną.
kaesjot 19 CZERWCA 2022 13:39
Otóż to… 🙁
R.S. 19 CZERWCA 2022 15:08
Dziś świece (spark plugs) są o wiele lepszej jakości jakieś 30 lat temu. Nie trzeba więc ich czyścić, regulować czy też tak często wymieniać jak dawniej.
kaesjot 19 CZERWCA 2022 15:06
To nie kiepska jakość produkowanych traktorów, a tzw. Plan Balcerowicza sprawił, że Zakłady Ursus celowo zniszczono, aby nie były one konkurencją dla takich zachodnich firm jak np. John Deere, Massey Ferguson, Kubota czy Deutz.
PAK4
19 CZERWCA 2022
14:42
Kluczem do zrozumienia procesu społecznego który obserwujemy w krajach bogatych, jest waska specjalizacja.
To działa w czasach normalnych, przewidywalnych, pozbawionych zawirowań.
Tyle że ten okres trwał – i to jedynie w Europie- zaledwie 70 lat.
Wchodzimy zdaje się w okres w którym szeroka gama umiejętności może się BARDZO przydać.
A niedostosowani, zbyt wolno adaptujący się do zmian środowiska?
Cóż, Darwinizm…..
Cywilizacja związana jest bezpośrednio z dostępem do coraz wyższych poziomów energii. Bez jej dopływu, więdnie.
Bariści, influencerzy, programiści, celebryci, moga być zbędni w nowym rozdaniu cywilizacyjnym.
Wymiana świecy to zdaje się jeden klucz, i wiedza w którą stronę należy kręcić…
Zbyt skomplikowane?
Wymiana „płynów ustrojowych” to wiedza w który otwór co lać.
Wymaga serwisanta?
Cóż….
EMP załatwi większość problemu nowoczesnych technologii opartych na elektronice.
Co to jest impuls elektromagnetyczny?
Jakie samochody przetrwają impuls elektromagnetyczny?
Mercedes W123 200D.
Fiat 126p.
Aston Martin DB5.
Toyota Corolla E90.
Citroen 2CV.
Skoda 120.
Porsche 356.
Mini.
kaesjot 19 CZERWCA 2022 14:51
Mój Ś+P wujek, maszynista parowozu, najprawdopodobniej nie słyszał o zasadzie naczyń połączonych, nie studiował analizy matematycznej ani termodynamiki etc., ale doskonale wiedział, że musi sprawdzać przede wszystkim stan wody w kotle przy pomocy wskaźnika, ktory działa na zasadzie naczyń połączonych i wiedział jak prowadzić parowóz, aby spalał on jak najmniej węgla i jednocześnie dojechał na czas do kolejnych stacji. Jakoś potrafił to wszystko zrobić, nie znając równań różniczkowych ani rozwiązania problemu minimaks. Czy matematycy mogą mi to wszystko wytłumaczyć?
wiesiek59 19 CZERWCA 2022 15:44
Niekoniecznie. Ja jakieś 30 lat temu miałem Nissana, gdzie były po dwie świece zapłonowe na cylinder i aby je wymienić, to trzeba było mieć w tym celu podnośnik albo kanał. W niektórych współczesnych samochodach to jest jeszcze bardziej skomplikowane. To już nie są czasy Syrenek czy Maluchów. I dobrze jest mieć do tego celu klucz dynamometryczny…
wiesiek59 19 CZERWCA 2022 15:44
FSO Syrena, FSO Warszawa – wszystkie modele. A FSO już nie ma…
wiesiek59 19 CZERWCA 2022 15:38
Otóż to. Znów liczyć się będą tylko REALNE i PRAKTYCZNE umiejętności…
PAK4 19 CZERWCA 2022 14:42
Młodzi może potrafią coś, czego starsze pokolenie nie kuma, ale to sa głównie zbędne i często społecznie szkodliwe umiejętności, np. jutjubowania, tłyterowania czy też influencjonowania. ;-)
Marcin Nowak 19 CZERWCA 2022 11:49
De facto są – konkurs świadectw maturalnych, tak jak np. w Australii. Ale powinny one wrócić, gdyż to uczelnia wyższa wie lepiej, kogo chce mieć za studenta, a nie szkoła średnia.
wiesiek59 19 CZERWCA 2022 10:46
Widać więc, że kasjerka w Biedronce jest w realnym kapitalizmie, w jego nadwiślańskiej wersji, dwa razy więcej użyteczna społecznie niż początkujący nauczyciel.
PAK4 19 CZERWCA 2022 10:06
1. Konkretnie do czego?
2. Ukraina to jest dziś jak Polska minus jej zalety ale plus dwa razy jej wady.
Ukłony!
SŁOWIANIN STANISŁAW 19 CZERWCA 2022 10:16
Tak samo jak Arabia Saudyjska, Emiraty, Katar, Izrael etc. – to są s-syny, ale NASZE, czyli „zachodnie” s-syny.
Orteq 19 CZERWCA 2022 9:48
To było ad personam, ale co masz do powiedzenia ad rem?
kaesjot 19 CZERWCA 2022 11:52
Odróżnij talenty rachunkowe od talentów matematycznych. Lem w de facto niemal autobiograficznym „Szpitalu Przemienienia” opisał debila, który był genialnym rachmistrzem, bo miał w głowie „takie siufladki, które się wysuwają”. Zdaje się, że Banach miał ten problem, że sprzedawczynie w sklepach były zdziwione, że liczą one w pamięci szybciej niż on – w całym Lwowie znany geniusz matematyczny pierwszej klasy…
wiesiek59 19 CZERWCA 2022 12:48
Matematyka może ćwiczy pamięć, logikę, umiejętność wnioskowania, kojarzenia etc. ale ponieważ oparta jest ona na nieweryfikowalnych aksjomatach, to należy ją nauczać tylko w ramach fizyki i innych nauk ścisłych. Co do chemii, fizyki etc, to nie ma tu dyskusji – kto ich nie zna, ten nie jest człowiekiem wykształconym, a tylko wykształciuchem, tzw. humanistą.
Natomiast nudne wkuwanie aksjomatów, definicji, wzorów, służy tylko degeneracji kory mózgowej.
act 19 CZERWCA 2022 7:54
Rachunek różniczkowy i całkowy działa, ale tylko dla niezbyt dużych i niezbyt małych liczb. I nie moja to wina, że jest to zamek zbudowany na ruchomych piaskach…
R.S. 19 CZERWCA 2022 14:09
Ludzie myślą analogowo a nie cyfrowo („dyskretnie”, jak to mówią naukowcy), a więc matematycy zawsze wydawać sie będą normalnym ludziom – dziwakami. Dawniej jeden myśliwy mówił drugiemu, że widział male, średnie albo duże stado bawołów, bo jak policzyć ilość bawołów w stadzie, jeśli one uciekają przed myśliwym i na dodatek wzniecają one przy tym tumany kurzu? Matematyka na dobre rozwinęła się zaś dopiero razem z kapitalizmem i jego kultem pieniądza, który ma jedną tylko zaletę – daje się łatwo policzyć…
6:1, 6:4.
Pierwsze takie liczby rzeczywiste , nie calkiem naturalne (-nie) ?
mpn 18 CZERWCA 2022 17:2
Generalnie, to aksjomaty Peano dowodzą, że arytmetyka z zerem nie jest symetryczna, a więc jest ona ułomna, przynajmniej z punktu widzenia matematycznej estetyki, gdyż operacje z zerem NIE są symetryczne: można bowiem dodawać zero, odejmować zero i mnożyć przez zero, ale nie można dzielić przez zero. Stąd też wynika potrzeba stworzenia nowej, lepszej arytmetyki, gdzie bedzie można dzielić przez każdą liczbę, a nie jak dziś, czyli z wyjątkiem zera. Stawiam butelkę dobrej whisky single malt każdemu, kto taką arytmetykę stworzy – ljkel2(at)netscape.net.
olborski 19 CZERWCA 2022 16:45
A co jest naturalne w matematyce?
kalvarya01
19 CZERWCA 2022
16:58
Jak dla mnie, laika, w matematyce naturalny jest WYNIK, zgodny za każdym razem.
Powtarzalny wynik to podstawa działania w swiecie rzeczywistym.
Powiedzmy mocniej, fundament na którym opiera się cała abstrakcyjna nadbudowa.
W innych naukach tego fundamentu czesto brak.
Ewentualnie, niewiele jeszcze wiemy bądź nie mamy narzędzi by to zmierzyć.
Historia, psychologia, kulturoznawstwo, nie ma fundamentów.
Jedynie hipotezy i domniemania.
Jakąś próbą była cybernetyka społeczna.
Ale, tego tematu nie sledziłem zbyt uwaznie.
Próby zaprogramowania społeczeństwa jednak trwają, intensywnie i nie szczędząc pieniędzy.
Stworzenie marionetek których zachowanie można przewidzieć, stymulować, to marzenie lalkarzy.
Nie wiem ale w tenisie nie wszystko i wszystko jednocześnie np – €113,785
Tzw tenis kwantowy nie symetryczny – ( zera mile widziane ale widziane niesymetrycznie , z jednej , przeciwnej strony ) – Speyside Single Malt
olborski 19 CZERWCA 2022 17:19
Marycha czy też może nawet Heroina? 😉
wiesiek59 19 CZERWCA 2022 17:15
Powtarzalne są np. obserwacje nocnego nieba, fazy Księżyca, przypływy i odpływy etc. a w matematyce powtarzalny jest zaś błąd wynikający z dzielenia przez zero, a więc matematyka współczesna jest mocno kulawa. Jak to już napisałem, jest ona ułomna, przynajmniej z punktu widzenia matematycznej estetyki, gdyż operacje z zerem NIE są symetryczne: można bowiem dodawać zero, odejmować zero i mnożyć przez zero, ale nie można dzielić przez zero. Stąd też wynika potrzeba stworzenia nowej, lepszej arytmetyki, gdzie bedzie można dzielić przez każdą liczbę, a nie jak dziś, czyli z wyjątkiem zera.
I zgoda co do reszty…
olborski 19 CZERWCA 2022 17:19
Żaden tenis nie jest symetryczny, gdyż nie ma tam remisów.
„Pamiętaj cholero – nie dziel przez zero” – przypomniało mi się ze szkoły.
I jeszcze jedno – pisane po rosyjsku :
Что я знаю о кругах = 3,1416
Tak nawiasem, to matematyka NIE jest nauką, a tylko jednym z wielu języków używanych przez nauki, głównie ścisłe, stąd też np. nie ma Nobla z matematyki.
Ponadto należy pamiętać, że matematyka oparta jest na aksjomatach, a więc odrzucając, zmieniając albo wprowadzając nowe aksjomaty, można tworzyć praktycznie dowolną ilość matematyk.
kaesjot 19 CZERWCA 2022 17:59
Pamiętam, a więc i nie dzielę ani też nie mnożę przez zero. ;-)
Cytuję: „długość okręgu o promieniu 1 jest niewymierna”. A mnie wychodzi praktycznie każdy pomiar długości każdego okręgu, którego długość nie przekracza długości mojej taśmy mierniczej. A ma ona kilka metrów długości. 😉
Takoż: „bez ciągłości zbioru liczb rzeczywistych nie sformułujemy rachunku różniczkowego i całkowego”. Otóż to, ale przecież- każdy zbiór liczb jest z definicji nieciągły, a „dyskretny”, gdyż nie ma bytów (entities), które byłby „łącznikami” między sąsiednimi liczbami – między każdą parą liczb na każdej osi liczbowej istnieje bowiem tylko szereg liczb i nic poza nimi. Np. pomiędzy 3 a 4 jest 3 i ½, między 3 i ½ a 4 jest 3 i 3/4 etc. Każdy zbiór liczb jest więc „dyskretny” tak jak materia, która też, jak wiadomo, składa się z cząstek, te składają się z atomów, atomy zaś z tzw. cząstek elementarnych (elektronów, kwarków, gluonów etc.), a więc nasza rzeczywistość materialna jest „dyskretna’ a nie ciągła.
A więc, jak to już pisałem, rachunek różniczkowy a więc też i całkowy, to są piękne zamki, ale zbudowane na ruchomych piaskach…
Przy mierzeniu wielkości fizycznych ( np. wymiarów ) istotna jest kwestia DOKŁADNOŚCI użytego narzędzia pomiarowego a ponadto POTRZEBNA jego dokładność. No i oczywiście ZGODNOŚĆ ZE WZORCEM jednostki miary.
kawaleria (kalvarya 01 )
„Marycha czy też może nawet Heroina? ”
…………
Nasz duch jest z nami bo pilnuje naszych skojarzeń ( np . kalvarya z kawaleria bo galopuje , umysłowo). Poznaj go .. własnego ducha
………………………..
„… ewolucja dlatego tylko mogła wytworzyć nasz mozg i nasza świadomość , ze realne istnienie tego , co określamy mianem ducha , umożliwiło jej powołanie w naszych głowach narządu dysponującego zdolnością polaczenia materialnego wymiaru z tym wymiarem duchowym „. skoro zatem ow duch realnie istniał przed nami i zarazem nie spadł z nieba , skąd, u licha wziął się w naszym dziwnym świecie ?
(….)
„Czyż nie jest zastanawiające , ze nasza tak przemożna chęć poznania świata zawsze w końcu zmusza nas do usiłowań poznania i zrozumienia samych siebie ? „(M. Ił. ze wstepu do H.vD.
…………………….
Wszystko co wydaje się dziwne i nie zrozumiale powinno przynajmniej cos nam przypominać … cos znajomego , albo cos co się takim wydaje . Kojarzyć się z czymś znajomym ..
Ale z własną d…ą nie może sie kojarzyć bo wtedy o poznawaniu świata nie ma mowy . Tak jak kiedy , duch z d..ą
kaesjot 19 CZERWCA 2022 20:53
Tak, ale wytłumacz to matematykom i humanistom. Oni przecież nigdy niczego na serio nie mierzyli i nie mieli na studiach ćwiczeń w laboratoriach fizycznych, chemicznych, elektrycznych (podzbiór fizycznych) etc.
olborski 19 CZERWCA 2022 20:59
Piękny, niemalże podręcznikowy przyklad „strumienia świadomości” schizofrenika. Ten „strumień świadomości” jest to albo zapis umysłowego przeżywania człowieka, nie tylko tego co aktualnie słyszy, widzi i czuje, lecz również jego myśli, skojarzeń, które mu się nasuwają. Wiąże się z tym zapis myśli i odczuć, narracja wyłącznie subiektywnymi odczuciami. Jest to także swoistym stylem, połączeniem umysłu rzeczywistej chwili i sumą odczuć jednej chwili. W strumieniu świadomości zdarza się też często relacja narratora wszechwiedzącego, który nie tylko opowiada myślami głównego bohatera, ale i wieloma innymi tworząc tzw. przestrzeń świadomości. Doskonale widoczne jest to w „Ulissesie” Joyce’a, gdzie w grę wchodzą myśli wielu opisywanych osób. Termin „strumień świadomości” bywa również stosowany również w odniesieniu do innych dziedzin sztuki. Koronny przykład filmu nakręconego za pomocą takiej techniki to „Osiem i pół” (1963) Federico Felliniego. Prawie że nic z niego nie zrozumiałem, ale bardzo mi się on podobał.
Pozdrawiam.
Ja, czyli ja (a może i my?).
olborski 19 CZERWCA 2022 20:59
Ta „kalwaria” to jest oczywiście nawiązanie do dziadów kalwaryjskich, czyli żebraków, proszących o jałmużnę po odpustach, pod kościołami – zjawisko, które praktycznie znikło w czasach PRL-u, ale odrodziło się pod nierządami solidaruchów. To jest też aluzja do mojej śmiesznie wręcz niskiej emerytury, którą wypłaca mi ZUS. Gdyby nie emerytury zagraniczne, na które zapracowałem na przymusowej emigracji, to została by mi dziś już tylko żebranina. Wielkie dzięki panom Wałęsie, Mazowieckiemu, Kaczyńskim, Tuskowi oraz, last but not least, Balcerowiczowi.
Proponuję dyskutantom obejrzeć film
https://www.youtube.com/watch?v=41iGGSQ-QHE&t=404s
w laboratoriach fizycznych, panuje duch zaokrąglania , przybliżeń po przecinku i współczynników bezpieczeństwa ( mech. gruntów )
Co kalwarii zero tak przeszkadza, kompleks jakiś czy co?
Pojawiła się też nowa definicja nauki, jest to dyscyplina w której przyznawane są Noble.
Czy jest jakiś górny limit bzdur na tym blogu? Może autorzy się dowartościowują przez kontrast.
izka,
milo Cie tu widziec 🙂
olborski 19 czerwca 2022 21:35
Pewien niemiecki uczony poza pracą naukową miał pasję – pszczelarstwo.
Przy swej daczy miał pasiekę składającą się z kilku uli. Pragnął podglądać życie pszczół „na bieżąco” i wymyślił sobie , że najlepiej będzie mógł to robić, gdy w ściankę ula wstawi sobie szklaną płytkę o wymiarach 200x200x5 mm. Ponieważ jedyną firmą branży „szklarskiej” jaką znał był Karl Zeiss Jena do niej wysłał zamówienie. Firma przyjęła to zlecenie pytając tylko o to, z jaką dokładnością mają wykonać.
Najdokładniej jak możecie – odpowiedział im profesor.
W mówionym czasie na daczę przyjeżdża samochód z dość duża skrzynią, którą tam wyładowali. Po otwarciu jej zobaczył, że w niej jest mniejsza skrzynka obłożona wełną drzewną a w tej mniejszej wyściełanej watą bawełnianą mocno owinięta płótnem owa zamówiona szklana płytka. Szczęka mu opadła gdy spojrzał w dostarczoną z towarem fakturę. Nie tylko pasieką ale i cała działkę z daczą musiał sprzedać by zdobyć pieniądze potrzebne na jej zapłacenie.
No ale sam chciał wykonania jej z największą jaką mogli dokładnością czyli do 1 mikrona. A to kosztuje !
Cz była ona w tym zastosowaniu niezbędna ?
A może doskonale spisałby się w tej roli kawałek zwykłej szyby okiennej pozyskany u miejscowego szklarza za butelkę piwa ?
Nie mam nic przeciwko liczbom, nawet rzeczywistym, ale gdyby skupić się wyłącznie na statystyce to jak się mówi strach się bać.
Zacytowane tu przykłady z amerykańskich miast mogą przyprawić o ból głowy tamtejszych statystyków.
Jeżeli ubywa połowa mieszkańców miasta, a zdecydowana większość tych co zostaje to kolorowi, to z tą białą mniejszością musi być naprawdę źle.
Podobno najwięcej obrońców Ukrainy pochodzi z Polski. Tu nie mam zdania, czy to dobrze czy źle o nas świadczy. Liczę na jakąś podpowiedź
Hej act, Ciebie też zawsze miło widzieć. I co ważniejsze czytać.
Ja tu już kiedyś pisywałam, ale przegoniła mnie jedna nieco szurnięta blogowiczka.
A teraz pojawił się kolejny typ z obsessive-compulsive.
Taki fajny matematyczny temat. Zupełna rzadkość wśród biologicznych dziwadeł. Zgadzam się, że liczby rzeczywiste muszą przede wszystkim istnieć, ale używać ich też można. Trzeba tylko trochę tolerancji.
Nasz tenisista klasyfikowany w drugiej dziesiątce ATP pokonał dzisiaj w finale turnieju tenisistę z numerem jeden.
To naprawdę duży sukces takie dwa do zera w meczu w dobrym stylu. Nawiasem mówiąc to piąty wygrany turniej
Drodzy Panowie, Drogie Panie,
myślę, że mnie nie zrozumieliście. Krytykujecie młodzież, brak jej umiejętności z perspektywy „bo ja umiem”. Czy zadajecie sobie pytanie, jak ta młodzież patrzy na Was — Dziadersów? Czy nie mówi: „bo ja umiem, a oni to jacyś przedpotopowi”? Bo dziadek nie potrafił drukarki podłączyć? Mejla wysłać? Załatwić sprawy w urzędzie online? Chodzi na pocztę by przelać pieniądze?
Ale — pokolenie to raz. Podkreśliliście pokolenie to i ja na nie wsiadłem. Ale nie tylko o to mi chodzi — chodzi mi o łatwość takich porównań, że ja coś umiem, a inni nie. Jak wielu jest tych innych? To ogólna tendencja czy jednostkowy przypadek? (W dyskusjach „naukowych” mówi się o „dowodzie anegdotycznym”, który w rozmowie potocznej często uchodzi za właściwy, a w nauce się go wyśmiewa.) No i wracając na początek — czy aby nie jest tak, że ja wielu rzeczy nie umiem, które dla innych są oczywiste? (W tej ostatniej roli występował ten Ursus. Dla wielu prowadzenie Ursusa jest oczywiste, ja zaś dorosłem całkiem dorosłego wieku, zanim dane było mi na niego wsiąść i nim pojechać.
Z dzisiejszą młodzieżą nie mam wielkich związków. Słyszę od wychowawców i opiekunów słowa raczej dobre — że najlepsza od dekad. Widzę, że z dekady na dekadę wzrastają ambicje edukacyjne — ci młodzi są już zwykle lepiej wykształceni niż My. Że jeśli coś niepokoi, to poziom problemów psychiatrycznych i liczba samobójstw (kolega-dyrektor liceum: u mnie, co roku jedno dziecko próbuje popełnić samobójstwo).
Uzdolnienia manualne? Przez pewien czas kaligrafowałem — fantastycznie odczułem wtedy, że przechodzę od klepania w klawiaturę w coś, czego moje ręce potrzebowały, a co przebywało w stanie uśpienia. Tak, każdemu polecę. Ale to nie jest tak, że w starszych pokoleniach wszyscy, a teraz nikt. Ci co potrzebują, radzą sobie pięknie.
Ukłony!
Tymczasem: Rosja zdobywa kolejne tereny w Donbasie
Siły rosyjskie przeprowadziły w niedzielę szturm na Toszkiwkę, kluczową ukraińską pozycję obronną w pobliżu Siewierodoniecka i Łysyczańska. Walka uwypukliła słabnącą obronę dwóch ostatnich miast w obwodzie ługańskim w regionie Donbasu, które nie są jeszcze kontrolowane przez Rosję.
Po tym, jak wojska rosyjskie otoczyły oba miasta, siły ukraińskie zajmują obecnie tylko niewielką część Siewierodoniecka. Ministerstwo Obrony Rosji nie skomentowało natychmiast sprawy Toszkiwki, ale poinformowało, że jego siły zajęły Metołkine, miasto położone na wschód od Siewierodoniecka.
Institute for the Study of War (dosł. Instytut Studiów Wojny) , waszyngtońska grupa badawcza, stwierdziła, że Rosja prawdopodobnie będzie w stanie zająć Siewierodonieck w ciągu najbliższych kilku tygodni, ale będzie się to wiązało ze znacznymi kosztami. Powolne tempo walk osłabia morale obu stron, a sekretarz generalny NATO, Jens Stoltenberg, ostrzegł, że wojna może trwać latami.
Żniwo śmierci: Wojna na Ukrainie przyniosła ogromne żniwo w postaci ofiar śmiertelnych. Nikt jednak nie jest pewien, ile wynosi ta liczba – wiadomo jedynie, że zginęło wiele osób.
New York Times
kaesjot 19 CZERWCA 2022 22:50 Dobre!
kwant25 19 CZERWCA 2022 21:30
Jutjub to sąsiednie blogi. Takie dla tych, do których należy Królestwo Niebieskie.
olborski 19 CZERWCA 2022 21:35
Bowiem np. każdy miernik ma swoją dokładność, a więc tylko kilka cyfr po przecinku ma sens. Kiedy studiowałem, to każdy pomiar (a był on wówczas analogowy) wykonywało się kilka razy i wyciągało średnią arytmetyczną z kolejnych wyników, zakładając, że te pomiary wykonano w takich samych warunkach.
izabella 19 CZERWCA 2022 22:04
Nie wtrącaj się do dyskusji, z której nic nie rozumiesz i do ktorej nikt ciebie nie zaprosił. I czy uważasz, ze polityka jako zawód, zajęcie, etc., i literatura to są dziedziny nauki?
ls42 19 CZERWCA 2022 23:04
Detroit to jest dziś USA „w pigułce”. A Ukrainy bronią dziś tylko faszyści: zwolennicy Bandery, UPA, OUN, ukraińskiej dywizji SS etc. Może są wśród nich jacyś byli Polacy – przecież wiemy jak dużo Polaków podpisało tzw. folkslistę. Wikipedia podaje za Wilhelm Deist, Bernhard R Kroener, Germany (Federal Republic). Militärgeschichtliches Forschungsamt, Germany and the Second World War, Oxford University Press, 2003, pp. 132,133, ISBN 0-19-820873-1, citing Broszat, Nationalsozialistische Polenpolitik, p. 134, że to było prawie 3 miliony osób.
Znasz też może taki wierszyk:
Kto ty jesteś? Volksdeutsch cwany.
Jaki znak twój? Krzyż złamany.
Kto cię stworzył? Zawierucha.
Co cię czeka? Gałąź sucha.
izabella 19 CZERWCA 2022 23:04
Powtarzam używając eleganckich, tzw. salonowych określeń: spadaj z tego blogu.
Swoją drogą, to tzw. liczby rzeczywiste oczywiście istnieją, ale tak samo jak np. elfy, krasnoludki, Hobbity czy też bogowie i boginie, czyli tylko w ludzkich umysłach. Reguły działań na liczbach są więc ustalane arbitralnie, jak to w matematyce, która, po raz kolejny powtarzam, NIE jest nauką. I wstrzymaj się kobieto z wydawaniem opinii na tematy, o którch nigdy nie będziesz mieć nawet najmniejszego pojęcia.
PAK4 20 CZERWCA 2022 5:11
To przeczytaj w całości to: „Krzysztof Wróbel na co dzień zajmuje się kręceniem filmów reklamowych, teledysków i reportaży. Niedawno aż się zagotował, gdy zobaczył w internecie reklamę mobilnej gry hazardowej. – W tym momencie uświadomiłem sobie, ile widuję dzieciaków wpatrzonych w telefony i grających na co dzień w autobusach, knajpach czy sklepach. Grają w kolorowe monety i inne skarby. Nic nie jest w stanie ich oderwać. Gdy tylko któryś z rodziców próbuje, dziecko reaguje niesamowitą agresją, krzyczy, syczy albo histeryzuje – opowiada. I dodaje: – Te gry są zaprojektowane tak, żeby jak najmocniej zaangażować uwagę i uzależnić mózg na poziomie podświadomym. Wszystko jest starannie przemyślane i intensywne: kombinacja kolorów, tempo gry, błyski, dźwięki…”
Więcej tu: https://weekend.gazeta.pl/weekend/7,177344,28581241,autokar-z-dzieciakami-przypominal-kasyno-w-las-vegas-slychac.html
kalvarya01,
zmien lekarza! Natychmiast!
PAK4 20 CZERWCA 2022 5:11
Dalej – jestem dziadkiem, ale takim dziadkiem który potrafi drukarkę nie tyko podłączyć ale i naprawić, e-mails wysłałem kiedy jeszcze miałem dostęp do Internetu poprzez system operacyjny DOS, załatwiam, jeśli się da, sprawy w urzędzie online a chodzę na pocztę by zapłacić rachunki, bo wolę je płacić gotówką. Po co wszyscy maja znać numery moich rachunków bankowych? Pomyślałeś o tym?
Dla mnie prowadzenie traktora czy ciężarówki to żaden problem, gdyż różnych zawodów się podejmowałem, a np. pracując w Afryce jako „software engineer” dla pewnej amerykańskiej firmy komputerowej, musiałem także czasami prowadzić ciężarówkę ze sprzętem komputerowym, gdyż dyrekcja nie dowierzała tubylcom, którzy mieli, jakby tu powiedzieć, aby nie ogłoszono mnie rasistą, dośc nietypowy styl prowadzenia pojazdów mechanicznych, który zagrażał stanowi ich ładunku.
Dalej – młodzi (jako całość, pomijając tzw. wyjątki potwierdzające regułę) NIE są dziś lepiej, a tylko znacznie gorzej wykształceni niż My. Piszę to jako wieloletni nauczyciel akademicki, także na tzw. przodujących polskich tzw. wyższych tzw. uczelniach (tzw. uniwersytetach). Zniesienie egzaminów wstępnych, płacenie przez Ministerstwo za ilość, a nie za jakość studentów oraz generalny upadek polskiej nauki na skutek tzw. Planu Balcerowicza, czy wreszcie dyrektywy unijne i tzw. polityczna poprawność – to wszystko spowodowało, że jakość obecnego magistra jest niż niższa niż jakość maturzysty z czasów PRL-u czy też z czasów II RP.
Niepokojąco wysoki poziom problemów psychiatrycznych i ogromna liczba samobójstw to jest zaś efekt powrotu kapitalizmu rynkowego – systemu gdzie człowiek jest człowiekowi wrogiem, gdzie liczy się nie inteligencja i wiedza, a tylko brak moralnych skrupułów, gdzie do władzy i bogactw dochodzą nie najlepsi, a najgorsi.
Uzdolnienia manualne się zaś zawsze przydadzą, czy to do gry na instrumentach muzycznych, czy też do malowania (ale w szeroko pojętych stylach „realistycznych” a nie „abstrakcyjnych”). Nie mówiąc już o drobnych naprawach czy ulepszeniach „w domu i zagrodzie”.
act 20 CZERWCA 2022 8:40
Znów nie masz nic do powiedzenia poza chamskim atakiem ad personam. 🙁
ls42 19 CZERWCA 2022 23:31
Przecież tenis uprawiany zawodowo to jest biznes a NIE sport. A on reprezentuje siebie i swoich sponsorów, a nie Polskę!
izabella 19 CZERWCA 2022 22:04
Mnie zero nie przeszkadza, ja tu tylko zwracam uwagę na fakt, że ceną za jego używanie jest niesymetryczność arytmetyki i różne problemy z jego używaniem, np. z dzieleniem przez zero, które są nierozwiązywalne w ramach aksjomatów przyjętych obecnie przez ogromną większość matematyków.
@kalvarya01, 8:39:
Ale to jest kwintesencja dowodu anegdotycznego — jedna osoba uogólnia swoje obserwacje, a potem ktoś to publikuje, po czym Ktoś jeszcze cytuje jako prawdę objawioną.
„Zagrożenia dzieci i młodzieży” nowymi technologiami doczekały się sporej literatury, ale to co do mnie dociera, to właśnie taka mniemanologia — bo mi się wydaje, bo widziałem młodzież w autobusie. (Uwaga: sam wyżej, pod tym blogiem, takie dwie obserwacje podrzuciłem; bo to czasem zabawne obserwować jak młode pokolenie wyciąga kalkulator by dodać 8 do 9…)
W każdym pokoleniu będziesz miał debili i wybitne jednostki. Jeśli należysz do plus minus elit (po kilkunastu „latach składkowych” emerytura ZUS nie musi tego oddawać), a oceniasz dzieci i młodzież średnią lub nawet gorzej (uwaga: młodzież z dobrych domów częściej jest dowożona przez rodziców ich samochodami do szkół i trudniej ją spotkać w autobusach… — pracowałem kiedyś na przeciwko „elitarnej” szkoły i widziałem ten przegląd luksusowych samochodów co rano przed lekcjami), no to trochę sorry, ale sam się prosisz o takie wyniki.
Podejrzewam zresztą, że jacyś psychologowie to już dawno rozgryźli jako błąd poznawczy, że zawsze inni mają więcej pieniędzy, zawsze inni wydają je bardziej niefrasobliwie, zawsze inni są mniej oszczędni, zawsze inni jeżdżą jak barany, zawsze inni są głupi, bo nie wiedzą czegoś co wiemy, itp. itd. Dlatego domagam się jakiś grup porównawczych, do których można by odnieść zachodzące zmiany — to raz; ale też dwa — oceny czy zmiany, jeśli zachodzą, rzeczywiście zachodzą na gorsze.
Np. Ls42 tu wrzuca uwagi o sukcesach Igi Świątech i (chyba) Hurkacza, który wczoraj pokonał Miedwiediewa, czyli tenisową jedynkę ATP. Czy, serio, dowodem upadku usportowienia polskiej młodzieży jest to, że jesteśmy świadkami największych triumfów tenisowych w historii tenisa w Polsce? Powiedziałbym, że takich subtelnych wskazówek, że pewne rzeczy w Polsce zachodzą całkiem fajne, także ze współczesną młodzieżą, rzeczywistość dostarcza nam całymi garściami.
Wyposażenie szkół w sprzęt IT czy czołgi Abrams … wygrały czołgi … Tak sobie myślę prywatnie … uczniom wystarczy tabliczka mnożenia na okładce zeszytu … po starszym rodzeństwie …
… 00 … jako liczba nie jest lekceważona … Tak sobie myślę prywatnie … w razie potrzeby każdy uznaje za rzeczywistą szansę ulżenia na ciele … nie tylko królowie …
PAK4 20 CZERWCA 2022 8:53
Ty też dajesz bardzo często jako „dowód” swoje własne obserwacje, ale ten tekst, który zacytowałem, opowiada o powszechnym zjawisku, które dziś niemal wszędzie można zaobserwować.
Poza tym, to miałem też do czynienia z potomkami tzw. elit, wykładając m. im ekonomię i zarządzanie na tzw. czołowych polskich tzw. wyższych uczelniach, a więc wiem z tzw. pierwszej ręki, że ich poziom jest dziś wręcz żałosny, tak jak poziom polskich „wyższych uczelni”. To jest opinia nie tylko moja, ale ogromnej większości polskich nauczycieli akademickich, tyle, że oni z wiadomych względów mówią o tym tylko w swoim gronie, a wiec ty nie masz szansy, aby się z nią zapoznać.
Popatrz też na miejsca, które najlepsze polskie „wyższe” uczelnie zajmują w światowych rankingach i jak daleko wyprzedziły nas w nich np. Chiny. To sa konkretne dane, publikowane latami. Oczywiście, że tym rankingom można wiele zarzucić, ale to one właśnie decydują, gdzie będą studiować najlepsi i najbogatsi, a więc które uczelnie otrzymają najwięcej pieniędzy z czesnego, od podatników i od sponsorów. To są fakty, a z nimi się nie dyskutuje.
Co do tenisa – uprawiany zawodowo to jest przecież biznes a NIE sport, a sympatyczny (niewątpliwie, oczywiście) Pan Hurkacz reprezentuje tylko siebie i swoich sponsorów, a nie Polskę.
I nie moja to wina, że tak bardzo chcesz żyć w „fool’s paradise” (a state of enjoyment based on false beliefs or hopes; a state of illusory happiness.). 🙁
SŁOWIANIN STANISŁAW 20 CZERWCA 2022 9:17
Dwa zera, czyli WC, to symbol a NIE liczba… 😉
@kalvarya01:
> Dalej – jestem dziadkiem, ale takim dziadkiem który potrafi drukarkę nie tyko podłączyć ale i naprawić […] Pomyślałeś o tym?
Kiedyś tu pisałem, że doceniam Twoje kompetencje na dostateczne na utworzenie własnego forum do pogaduszek w internecie. Tylko znowu — porównywałeś wyobrażoną zbiorowość, której ogląd wyciągnąłeś z jednostkowych przypadków z wyidealizowanym sobą. Pisałem o tym w odpowiedzi wyżej, a tu mogę dodać, że moje typowe doświadczenia z Twoimi rocznikami (OK, to rocznik mojej Mamy był), ograniczają się do ludzi nieudolnie wykładających rzeczy na kasie, zamulających kolejki na poczcie, albo proszących o pomoc z zepsutą drukarką, po czym okazuje się, że wypadła wtyczka od prądu. Z takich jednostkowych obserwacji mam równe Tobie prawo oceniać całe pokolenie.
Zresztą, Szanowny Pan tak bardzo chwali swoje kompetencje, a potrzebuje dyskusji pod blogiem w zastępstwie forum dyskusyjnego. Co to za kompetencje cyfrowe?
> Dalej – młodzi (jako całość, pomijając tzw. wyjątki potwierdzające regułę) NIE są dziś lepiej, a tylko znacznie gorzej wykształceni niż My.
Kiedy byłem małym chłopcem, hej, studiowało mały odsetek. Zresztą… ja trafiłem do fajnego liceum, gdybym nie trafił, a wzorował się na rówieśnikach z sąsiedztwa, raczej nie przyszłoby mi do głowy, że można studiować, nawet będąc piątkowym uczniem. Normą było kończenie na szkole średniej, zwykle zawodowej. W stosunku do lat 80-tych liczba studentów wzrosła nam ponad 4 razy.
Wiem, napiszesz, że poziom studentów spadł. Ja bym się nawet nie zdziwił — tylko powtórzę — 4x. Pomyśl o materiale ludzkim przy takim otwarciu szkół. I o tym, że za wykształceniem jednak idą ambicje.
Kolejna rzecz, którą obserwuję — pokolenie moich rodziców uważało tytuł inżynierski, czy magisterski za szczyt wykształcenia — do dziś śmieszą mnie na cmentarzu te podkreślenia, że ktoś był magistrem przy nazwisku; w moim już wypadało mieć dwa ukończone kierunki lub doktorat; a obecni młodzi często wybierają studia na dobrych uczelniach zachodnich. (Kolejne pytanie: jak zmieni się poziom IQ kandydatów na studia, gdy najzdolniejsi pojadą studiować za granicą?)
(I jeszcze jedno pytanie, przy okazji: gdzie studiują dzieci polityków-krytyków Zachodu z Rosji, czy z Polski?)
> Zniesienie egzaminów wstępnych, płacenie przez Ministerstwo za ilość
Znajomi pracowali na dość prestiżowej uczelni, a wiązali koniec z końcem dorabianiem na prywatnej „drukarni dyplomów”. W prywatnych rozmowach, gdzie lepiej się kształcić mówili, że prywatna uczelnia daje lepsze warunki (sprzęt itp.), przy równie dobrej kadrze (patrz oni sami), ale nie stawia progów przychodzącej młodzieży, przez co jest mniejsza konkurencja i, generalnie, mniejsze ambicje. Że jeśli ktoś ma ambicje i chce pracować, to szkoła prywatna byłaby lepsza; jeśli potrzebował motywacji otoczenia — to państwowa.
Co notuję, bo rzeczą, która mi się nie podoba, jest pewna wzgarda dla wykształcenia i nauki, oraz uczenie się dla dyplomu, a nie dla wiedzy. Nie wiem jednak, czy tego jest więcej niż było kiedyś. Wiem tylko, że jedną z rzeczy, która tak u Ciebie i paru innych się nie podoba, jest właśnie ta wzgarda dla wiedzy — uważam, że gardząc powiedzmy „gender studies” nie różnisz się od studenta, który idzie na zajęcia po dyplom, a całe „wyższe wykształcenie”, czyli zbudowanie horyzontów intelektualnych, pewnej filozofii dziedziny wiedzy itp. ma za stratę czasu.
> jakość obecnego magistra jest niż niższa niż jakość maturzysty z czasów PRL-u czy też z czasów II RP.
Jeszcze mam jedną uwagę, oprócz tej liczby magistrów kiedyś i teraz: moja licealna koleżanka skończyła matematykę. Kiedyś do niej przyszło jej własne dziecko, z zadaniem z podstawówki z matematyki do rozwiązania. I koleżanka się wyłożyła. Bo zadanie było bardziej na kreatywność i inteligencję, niż na wykute formułki, czy sprawność obliczeniową. Tak się zastanawiam, czy w tej całej krytyce młodych w ogóle zauważasz, że w tym kierunku zmienia się model edukacji — uczenia kreatywności raczej, niż wbijania formułek do głowy?
> Nie mówiąc już o drobnych naprawach czy ulepszeniach „w domu i zagrodzie”.
No właśnie, mam za sobą weekend z bólem głowy nad kwestiami hydraulicznymi, których w przeciwieństwie do elektrycznych, nigdy nie lubiłem… Ech…
@kalvarya01:
Chcesz moją własną obserwację za dowód? Cóż, znam ocaleńca, który uciekł przed Ukraińcami podczas rzezi wołyńskiej. Potem przez lata wyklinał Ukrainę i jej barwy narodowe, nawet ze śląskimi nie można się było pokazać. Dzisiaj jest, na ile zdrowie pozwala, wielkim sojusznikiem niepodległej Ukrainy przeciwko nieusprawiedliwionej agresji Putina. Q.E.D. 😀
PAK4 podaj miejscowość … tego uciekiniera przed banderowcami … Ukraińców zostaw w spokoju … bo też byli ofiarami jak Polacy za kolaborację … Tak sobie myślę prywatnie … Ukraina jest nadal banderowska jak Gruzja stalinowska … choć na czas wizyt pożytecznych idiotów z tzw. zachodniej cywilizacji symbole wynoszone są na strych …
@SŁOWIANIN STANISŁAW:
Ukraina banderowska, Gruzja stalinowska, Rosja carska-ochranna, Polska faszyzująco-endecka. Mogę ubolewać, ale do krytyki to trzeba by coś lepszego reprezentować.
Podać miejscowość: ale którą dawną, nową?
@PAK4
Dwa przypadki z relacji świadków rzezi wołyńskiej:
1. Ojciec Ukrainiec pyta się syna, po co ostrzy siekierę.
Aby matkę ubić – odpowiada syn
Matkę chcesz zabić ? – spyta zdziwiony ojciec
Jaka ona matka – przecież to Laszka jest – odpowiada mu syn.
Wzburzony ojciec wyrwał mu siekierę i własnoręcznie zabił nią swego syna.
2. Gdy do domu mieszanej , ukraińsko polskiej rodziny przyszli banderowcy to ojciec Ukrainiec własnoręcznie zabił swą żonę Polkę a córki roztrzaskał o ścianę domu, bo to też Laszki były. Wtedy obowiązywała tam zasada, że syn dziedziczył narodowość ojca a córki – matki.
Który zatem wg Ciebie przypadek należy uznać za reprezentatywny ?
Ja pamiętam , jeszcze ze szkoły, że „wyjątek nie czyni reguły”
Ps.
Było także powiedzenie, że „wyjątek potwierdza regułę”
Zatem, który wyjątek z wyżej przytoczonych jaką regułę potwierdza ?
A propos braku symetrii wobec zera we współczesnej nam arytmetyce. Piszę o tym gdyż wiem, jak wielką wagę przywiązują matematycy, a także fizycy czy chemicy do symetrii, a matematycy także do estetyki dowodu czy twierdzenia. Pamiętam, że będąc programistą wówczas jeszcze nie komputera a EMC Odra 1304 na dawnym SGPiS-ie, dziś znów jak za Sanacji, SGH, to kolega matematyk „zredukował” mój program do obliczeń statystycznych (napisany w Algol-u albo Fortrnan-ie) do mniej niż jego połowy, ale ja mu wyjaśniłem, że ten program celowo był tak napisany, aby nawet poczatkujący studenci mogli go zrozumieć i zmodyfikować. Kiedy zaś pracowałem dla HP, to byłem tzw. tool smith, czyli pisałem programy języku C (wówczas jeszcze bez plusów) pomagające pisać programy dla innych programistów. Ale kiedy nadeszła recesja, to jakiś geniusz z dyrekcji skasował moj etat, argumentując to tym, że takie programy to mogą inni programiści pisać dla samych siebie, mimo iż moj szef to właśnie mnie wyznaczył do tego zadania, gdyż ja pisałem te programy tak, że moi koledzy (a czasami nawet i koleżanki) mogli te programy z łatwością zmieniać czy też adoptować do innch celów etc., mimo iż z punktu widzenia estetyki rozumianej tak ją rozumieją matematycy, to one jakby były „przegadane’, a więc i tym samym „brzydkie”. Ale przecież beauty is in the eye of beholder.
PAK4 20 CZERWCA 2022 9:28
Jak się ten „twój” Polak nazywa, gdzie on mieszka etc. I o jakiej nieusprawiedliwionej agresji piszesz? O napadzie USA na Koreę, Kubę i Wietnam, czy też na Irak, Afganistan czy Syrię? I jeszcze to – kiedy na początku XXI pracowałem na prywatnej wyższej uczelni na Cyprze zwanej American College, to miałem tam „mnóstwo za bardzo” studentów i studentek z Zimbabwe. Wszyscy oni mieli kupę pieniędzy, jeździli pięknymi samochodami, lepszymi niż mój, a zarabiałem tam wtedy sporo. A w prasie i TV było wówczas pełno informacji o tym, jak to gospodarka Zimbabwe leży na obu łopatkach, o tym że dolar Zimbabwe jest praktycznie bez siły nabywczej na skutek hiperinflacji etc. etc. Jak to wyjaśnisz?
PAK4 20 CZERWCA 2022 9:26
1. Znów dajesz swoje niereprezentatywne obserwacje jako dowód na stan rzeczy. To jest tzw. fallacy of composition, czyli wyciąganie fałszywych wniosków o całości na podstawie znajomości tylko jego niereprezentatywnej części.
PAK4 20 CZERWCA 2022 9:26
2. To załatw mi w „Polityce” umieszczenie mojego blogu tuż obok blogu „naszych” naukowców. Stworzyć blog to jest łatwo i robiłem to już wiele razy, ale jak z nim dotrzeć do czytelników? Czy wiesz, ile to dziś kosztuje?
PAK4 20 CZERWCA 2022 9:26
3. Znów nie rozumiesz, że wyższe uczelnie otwarto w Polsce po roku 1989 dla każdego absolwenta szkoły średniej w ramach tzw. Planu Balcerowicza – tyle że nie jak dawniej jako miejsca kształcenia przyszłych elit, ale jako „przechowalnie” i „wytwórnie” bezrobotnch. Wiadomo też, a co łatwo jest sprawdzić, że tylko góra 10% każdej większej populacji ma predyspozycje do ukończenia studiów wyższych, a jeszcze mniej na kierunkach, gdzie wymagane jest ścisłe, czyli naukowe myślenie.
PAK4 20 CZERWCA 2022 9:26
4. Znów błędnie generalizujesz na podstawie swoich niereprezentatywnych obserwacji, pisząc że „obecni młodzi często wybierają studia na dobrych uczelniach zachodnich”. To dotyczy przecież tylko garstki potomków tzw. elit! Przecież ogromna większość obecnych młodych Polaków wybiera studia na złych uczelniach polskich, bo na nic innego nie jest ich po prostu stać!
PAK4 20 CZERWCA 2022 9:26
5. Pytasz się, gdzie studiują dzieci polityków-krytyków Zachodu z Rosji, czy z Polski? Ci z Rosji to na ogół w Rosji, a z Polski to różnie bywa. Uniwersytet Łomonosowa w Moskwie zajął bowiem w światowych rankingach następujące miejsca:
ARWU World 93
QS World 84
THE World 189
Dla porównania UW:
ARWU World 401-500
QS World 308
THE World 601-800
PAK4 20 CZERWCA 2022 9:26
6. Znów opierasz się na swoich niereprezentatywnych obserwacjach. A ja wiem z mojej wieloletniej praktyki jako wykładowca akademicki, że w Polsce, to na prywatnych „uczelniach” tylko kupuje się dyplomy, a studiuje tylko na państwowych.
PAK4 20 CZERWCA 2022 9:26
7. Te „gender studies” to jest klasyczna wręcz pseudonauka, tak jak np. astrologia czy teologia.
Rozkład inteligencji w populacji jest zawsze zgodny z Krzywą Gaussa….
Po wojnie, dzięki bezpłatnym wyższym uczelniom, szkolom średnim,
wyższe wykształcenie zdobyło 7% populacji, średnie 13%.
Cała reeszta to zawodówki i niewielki procent podstawowego.
Idea, że 50% populacji zdobędzie wykształcenie wyższe, jest ideologią dość kosztowną.
NIE MA takiej ilości ludzi zdolnych, by ją zrealizować bez obniżenia poziomu kształcenia.
Sprywatyzowanie uczelni obniża jakość z prostego powodu.
Czesne jest podstawą bytu takiego tworu.
Oblanie jełopa godzi w finanse.
Po 30 latach na wielu stanowskach mamy absolwentów tychże dziwacznych tworów. Jak wyglądają efekty, każdy widzi.
Poziom tych ludzi bardzo ladnie wyszedł na tasmach „U Sowy”….
Ps.
Własny blog to miesięczny koszt 20- 30 000 zł.
Te nieprawomyslne zostały w wiekszości zablokowane.
Były zbyt krytyczne wobec panującej ideologii czy poziomu naszych Ukochanych Przywódców.
Peferuje się myślenie stadne.
Przy tym poziomie edukacji cel został osiągnięty z nawiązką.
PAK4 20 CZERWCA 2022 9:26
8. NIE, dziś nie uczy się w szkołach polskojęzycznych kreatywności a tylko tresuje w nich uczniów, szczególnie zaś na zajęciach z religii, gdyż kreatywni, racjonalnie myślący obywatele są zagrożeniem dla obecnych, prozachodnich nierządów ciemniaków typu Dudy, Morawieckiego, Ziobry czy Kaczyńskich, o Wałęsie już nie wspominając. To za „moich” czasów na egzaminie wstępnym na matematykę na UW były właśnie pytania na ową kreatywność. Ale dziś nie ma już przecież egzaminów wstępnych na wyższe studia…
PAK4 20 CZERWCA 2022 9:26
9. Służę pomocą – ljkel2@netsacpe.net. 🙂
wiesiek59 20 CZERWCA 2022 11:32
1. Napisałem już, że wyższe uczelnie otwarto w Polsce po roku 1989 dla każdego absolwenta szkoły średniej w ramach tzw. Planu Balcerowicza – tyle że nie jak dawniej jako miejsca kształcenia przyszłych elit, ale jako „przechowalnie” i „wytwórnie” bezrobotnych. Wiadomo też, a co łatwo jest sprawdzić, że tylko góra 10% każdej większej populacji ma predyspozycje do ukończenia studiów wyższych, a jeszcze mniej na kierunkach, gdzie wymagane jest ścisłe, czyli naukowe myślenie.
2. Takoż – stworzyć blog to jest łatwo i robiłem to już wiele razy, ale jak z nim dotrzeć do czytelników? A na taki za 20 złotych miesięcznie, to przecież nikt praktycznie nie dotrze…
3. Generalnie to zgoda.
@kaesjot, @PAK4
Zeby tylko ten taki jeden tutaj nie dopatrzył się ‚nie na temat’ problemu…
Nasze przypominanie banderowców, rzezi wołyńskiej, oraz innych grzechów ukraińskich z historii, na nic dzisiaj. Zapanowała bowiem w Europie, głownie, powszechna mania popieranie wszystkiego co się wiąże ze ‚słuszną’ walka Ukrainy z agresja Putina.
Czy ktoś w Polsce dzisiaj odważny się pisnąć nt. DLACZEGO Putin się zdecydował na te agresje w 2022 roku? Po utworzeniu, w 2014 roku, trzech rosyjsko- języcznych republik ‚ludowych’ na wschodzie Ukrainy? Bo ten nie polski choc z polska brzmiacy Zyd, wiekowy bardzo, się odważa
https://truthout.org/articles/chomsky-us-is-playing-with-the-future-of-civilization-in-order-to-weaken-russia/?eType=EmailBlastContent&eId=ecf13d52-7ec5-4d86-b6b4-fcd416c92a9d
„W 1997 r. Clinton zaprosił tzw. kraje wyszehradzkie – Węgry, Czechosłowację i Rumunię – do NATO. Rosjanom się to nie spodobało, ale nie zrobili większego zamieszania. Potem dołączyły kraje bałtyckie – i znowu to samo. W 2008 r. drugi Bush, który był zupełnie inny niż pierwszy, zaprosił do NATO Gruzję i Ukrainę. Każdy dyplomata amerykański doskonale rozumiał, że Gruzja i Ukraina to dla Rosji czerwona linia. Będą tolerować ekspansję w innych miejscach, ale te kraje leżą w ich geostrategicznym sercu i nie będą tolerować ekspansji tam. Kontynuując ten wątek, w 2014 r. na Majdanie doszło do powstania, w wyniku którego usunięto prorosyjskiego prezydenta, a Ukraina zbliżyła się do Zachodu.
Od 2014 r. USA i NATO zaczęły dostarczać Ukrainie broń – zaawansowane uzbrojenie, szkolenia wojskowe, wspólne ćwiczenia wojskowe, działania mające na celu włączenie Ukrainy do dowództwa wojskowego NATO. Nie ma w tym żadnej tajemnicy. To było całkiem otwarte. Ostatnio chwalił się tym Sekretarz Generalny NATO, Jens Stoltenberg. Powiedział: To jest to, co robiliśmy od 2014 roku. Oczywiście, jest to bardzo świadoma, wysoce prowokacyjna akcja. Wiedzieli, że wkraczają na teren, który każdy rosyjski przywódca uważał za niedopuszczalne posunięcie. Francja i Niemcy zawetowały tę decyzję w 2008 roku, ale pod naciskiem Stanów Zjednoczonych została ona utrzymana w porządku obrad. NATO, czyli Stany Zjednoczone, przyspieszyło faktyczną integrację Ukrainy z dowództwem wojskowym NATO.”
Sa i inne przyczyny, z powodu których Putin dokonał inwazji na Ukraine. Noam Chomsky nie tylko je wymienia. On je również uważa za całkowicie te inwazje usprawiedliwiające!
Takiego stanowiska raczej trzeba dzisiaj szukać w świecie nie opanowanym przez narracje z Waszyngtonu nam narzucana. My, razem z około 20 procent populacji świata, zachodniego głownie, ja łykamy bez oporu większego. Natomiast większość ludności świata – ta mieszkająca w Chinach, Indiach, Pakistanie, Bangladeszu, Indonezji, Afryce z RPA na czele – nie poparła żadnej rezolucji ONZ, potępiającej Rosję za te inwazje.
Trudno nawet wyguglowac takie kwiatki
Na tle historycznych zbrodni jankesów od rdzennej ludności zamkniętej w rezerwatach począwszy … konflikt o Donbas jawi się jak wojna domowa … czy ciupażenie na zabawie górali … Tak sobie myślę prywatnie … tradycja wymaga ofiar … walki o miedzę …
@PAK4
„W Arabii Saudyjskiej homoseksualna orientacja jest surowo zabroniona. Zgodnie z krajową interpretacją prawa islamskiego dobrowolne zachowania seksualne osób tej samej płci są karane śmiercią lub chłostą, w zależności od wagi sprawy. Sprzeczne z prawem jest również noszenie przez mężczyzn kobiecych ubrań”.
Czy państwa UE albo USA zrywają stosunki dyplomatyczne z Arabią Saudyjską? Wstrzymują handel? Ogłaszają jakieś sankcje? Przecie wielka krzywda tam się dzieje!
https://podroze.gazeta.pl/podroze/7,114158,28600492,teczowe-przedmioty-sa-zakazane-w-arabii-saudyjskiej-promuja.html#do_w=57&do_v=428&do_st=RS&do_sid=750&do_a=750&s=BoxOpLink
Orteq 20 CZERWCA 2022 12:09
Wiem o Chomsky’m. Znajomi (Anglosasi, typowi WASPs, czyli NIE Polonusi) z USA ciągle mi o nim przypominają, kiedy przypominam im zbrodnie amerykańskiego imperializmu.
Pozdrawiam,
LK (Lech Kalwaryjski)
@kaesjot, kalvarya01:
Oui. Widzicie, ja nie wiem, czy ten ojciec mojego znajomego, z którym mam przyjemność czasem się spotkać, jest reprezentatywny. I to mnie różni od tego, co tu piszecie tak często i gęsto. Wy wiecie, że Wasze przykłady czegoś dowodzą. Ja tego nie wiem. Ja tylko się cieszę, że ten ojciec mojego znajomego, okazuje się takim fajnym i rozsądnym człowiekiem.
@kalvarya01:
> To dotyczy przecież tylko garstki potomków tzw. elit!
Oczywiście, choć moi znajomi to klasa średnia, a nie wyższa. Tyle, że z dużym kapitałem kulturowym. Ktoś taki, jaki w moich czasach mógł posyłać dziecko na polski uniwersytet.
> Uniwersytet Łomonosowa w Moskwie zajął bowiem w światowych rankingach następujące miejsca
84-189 miejsce na świecie? Widzisz co piszesz? :LOL: Dobre kilkadziesiąt miejsc dla uczelni głównie zachodnich — zerkam na ARWU: Harward, Stanford, Cambridge, MIT, UoC, Pinceton, Oxford… Pierwszy „niezachodni” jest Unwiersytet Tokijski, 24 miejsce; a potem Tsinghua (28). Teraz upraszam, porównać te rankingi do liczby ludności.
> Dla porównania UW
No i? Znowu jakieś dziwne myślenie, że skoro uważam zachodniej uniwersytety za lepsze od wschodnich, to chwalę UW…
Polski model uniwersytetu i polskie finansowanie uczelni nie dadzą nam pierwszej setki. Za Gowina był taki pomysł by PAN nazwać uniwersytetem — wtedy mielibyśmy uniwersytet w pierwszej setce. Ale to byłoby tylko propagandowe.
Swoją drogą, dalej nie odpowiadasz na moje pytanie, gdzie wysyłają swoje dzieci na naukę, czy robienie kariery, ci różni krytycy Zachodu. Zachód jest zły — to takie hasło dla biednych do manipulowania, bo sami chcieliby by tak żyły ich dzieci.
> NIE, dziś nie uczy się w szkołach polskojęzycznych kreatywności a tylko tresuje w nich uczniów, szczególnie zaś na zajęciach z religii
Może nie jestem na bieżąco, ale katecheza w polskich szkołach nie przekracza 50% godzin lekcyjnych…
> Takoż – stworzyć blog to jest łatwo i robiłem to już wiele razy, ale jak z nim dotrzeć do czytelników? A na taki za 20 złotych miesięcznie, to przecież nikt praktycznie nie dotrze…
Więc o to chodzi — pasożytować na wpisach Gospodarzy by szerzyć kłamstwa? Niby wiedziałem, ale jakoś się człowiek łudził…
BTW. Bloga można założyć za darmo. Komentując, także tu, możesz podać linka do swojej strony i taką choćby, ją promować. Ale, sorry, trzeba jeszcze z sensem pisać.
> Czy państwa UE albo USA zrywają stosunki dyplomatyczne z Arabią Saudyjską?
Czy Arabia Saudyjska, zaatakowała, powiedzmy, Iran i próbowała przeprowadzić desant powietrzny na Techeran by „zdeszyityzować” Persów? Jakoś nie zauważyłem…
@Orteq:
> [Chomsky] je również uważa za całkowicie te inwazje usprawiedliwiające!
Zieeeew, a ja nie.
Chomsky popełnia błąd, który popełniają niektórzy z Was — w odpowiedzi na propagandę Zachodu, przestawił sobie w głowie zwrot wektora sympatii na anty. Takie przypadek jak system immunologiczny pracuje za bardzo. Bo że reaguje na propagandę — OK, popieram. Ale że zamiast szukać prawa i sprawiedliwości w swoich osądach, przyjmuje postawę antyzachodniej propagandy. Innymi słowy: równa do Fox News, Kato, RM, albo FOR 😛
@PAK4
Poziom uczelni wyższych na tzw. Zachodzie musi się pogarszać, gdyż tam do pracy na stanowiska naukowo-dydaktyczne przyjmuje się dziś nie najlepszych, ale kobiety, gejów, Murzynów etc. i finansuje „gender studies” zamiast nauk ścisłych. Z tego też powodu zrezygnowałem w Komisji Europejskiej z oceniania podań o granty na badania naukowe.
Ciesze się ze wiesz o Chomskim, Lechu (@12:48). Ja sie ciesze, ze on wciąż żyje..
Zas tu bezkrytyczna AlJazeera proponuje lata trwania wojny na Ukrainie. Z nauka czy bez. O naukowcach nie wspominając, jako ze ci na wojnie
https://www.youtube.com/watch?v=t2cwVbNAR10
Mijają cztery miesiące od inwazji Rosji na Ukrainę.
Szef NATO i premier Wielkiej Brytanii ostrzegają, że konflikt może trwać latami, ponieważ Rosja koncentruje się na zajęciu strategicznych miast we wschodniej Ukrainie.
Delegaci ukraińscy i rosyjscy po raz ostatni rozmawiali twarzą w twarz w Stambule w marcu.
Od tego czasu negocjacje dyplomatyczne nie przyniosły większych postępów, a obie strony twierdzą, że osiągnęły impas. Czy konflikt może zostać zakończony na drodze dyplomatycznej?
Żydzi ukraińsko-amerykańscy, którzy powrócili z USA na Ukrainę, będącą w stanie wojny z Rosja, musza słuchać Zelenkiego i Bidena – a nie Chomskiego – jeśli wciąż wierzą w sprawiedliwość tej wojny
izabella,
sama widzisz…pogadalim.
Trzymaj sie 🙂
@Gospodarze:
A propos dzielonego newsa na FB — dwa lata temu w sakwie rowerowej znalazłem takiego pasażera na gapę:
https://1.bp.blogspot.com/-jdN2lxhNVg0/XuJcUH4DPcI/AAAAAAAA9Wk/saj5CAjL82YW3ooDw4T4yp8Yy6QjYXu6wCLcBGAsYHQ/s1600/DSCF2489.JPG
I znowu kook, psycho troll rozwalil kolejny blog.
brrrr….
@kalvarya01:
Ja sobie więcej tego Rankingu Szanghajskiego pooglądałem. Robią Chińczycy, by się dowiedzieć kogo ścigać i naśladować. Przed Uniwersytetem Moskiewskim są uczelnie z Danii, Norwegii, Szwecji, Finlandii, czy Szwajcarii. Państw, które licząc PKB, czy ludność, nie mogą się ścigać z Rosją.
Tak, że ten tego, upadek intelektualny Zachodu wciąż jest dużo, dużo lepszy od wzlotów intelektualnych Wschodu…
Z bożą pomocą woda wróciła na Krym … Tak sobie myślę prywatnie … festina lente … ! …
@act, Izabella, markot, maly fizyk, Gospodarze, G82
Don’t give up
Sięgnąłem po książkę pokryta kurzem „Fixed-Point Toolbox” i natrafiłem na problem językowy.
Otóż po angielsku liczby stało przecinkowe można zapisać według schematu
Real-world value = (slope x integer) + bias
gdzie:
Slope = fractional slope x (2 ^ fixed exponent)
No I właśnie jak przetłumaczyć na polski bias?
Google podpowiada słowo: stronniczość numeryczną co trochę brzmi jak mambo jumbo
Z kolei, jeśli zamiast bias użyjemy słowa offset to translator podpowiada przesunięcie.
Ja bym raczej zastosował piedestał numeryczny, ale może ktoś podpowie.
PAK4
20 CZERWCA 2022
14:57
Bzdury.
Zachód stworzył sobie samooceniający się system.
Bazuje na faktach sprzed 50-100 lat, kiedy rzeczywiście dominował w przestrzeni naukowej i technicznej.
Pomagały tej pozycji gigantyczne dotacje przekazywane przez agencje rzadowe i koncerny.
Również, drenaż mózgów z wszystkich stron świata.
Ten trend powoli się kończy.
Ostatnie 30 lat to schyłek mitu wykreowanego przez celową akcję dezinformacyjną.
Biegun magnetyczny nauki powoli przesuwa się na wschód.
Proces może potrwać oczywiście jeszcze kilkanaście lat.
Ale jest nieubłagany.
Zaczyna się zwykle od zrujnowania podstaw- poziomu szkół podstawowych.
Klasy przepełnione imigrantami zaniżają poziom ogólny nawet renomowanych szkół.
Azjatyccy studenci na uczelniach zachodnich stanowili podobno nawet 50% studentów, płacąc wysokie czesne.
Głownie, w naukach ścisłych, biologii, inżynierii.
Większość z nich podejmowała studia doktoranckie, staże w najlepszych koncernach przemysłowych- które zresztą sa w zaniku.
Bez tego zastrzyku intelektualnego, zachód nie ma szans w wyścigu na przełomowe technologie.
„Nie ma kim robić, panie majster”….
Ranking oparty na cytowaniach w uznanych ANGLOJĘZYCZNYCH pismach naukowych, recenzowany przez anglosaskich uczonych, anglosaskie redakcje?
Prawdopodobieństwo obiektywizmu nie przekracza raczej 50%.
Klub Białych nie przyjmuje kolorowych.
Orteq
20 CZERWCA 2022
13:44
Chomsky po osiągnięciu godnego wieku 93 lat, zaczyna nieco zmieniać swoje lewicowe i antyimperialistyczne poglady.
Osobiście wolę 99 latka- Kissingera.
On nie zmienia poglądów.
Jest racjonalny w swych ocenach.
A ten nowy narybek który stworzył z pociotków pani Nuland jakies studium wojny, kolejne kółko wzajemnej adoracji dojące ciężką kasę, nie jest warte minuty uwagi.
Wysoko opłacane błazny na dworze króla….
R. S.
courtesy Politechnika Poznanska:
bias = dodanie do sygnalu stalej wartosci.
Nie pytaj, bo nie wiem, z czym to sie je.
@wiesiek59:
> Zachód stworzył sobie samooceniający się system.
Ten ranking jest CHIŃSKI. Dyskutuj z Chińczykami, dlaczego popierają samooceniający się system.
> Bazuje na faktach sprzed 50-100 lat, kiedy rzeczywiście dominował w przestrzeni naukowej i technicznej.
Wybacz, ale jeśli nie Zachód to kto teraz dominuje w nauce i technice? Japonia? Chiny? Bo chyba nie Rosja.
Nawiasem mówiąc, pokaż mi dobry silnik lotniczy made in China.
Chińczycy (a wcześniej Japończycy, czy Korea) bardzo mądrze się modernizują. Może Japonia i Korea już doszły do poziomu „Zachodu”, ale też imitując go, przyjęły zasady jego filozofii politycznej.
Chiny robią wielkie postępy — jestem pod wrażeniem. Ale — postępy, to jeszcze nie osiągnięcie poziomu Zachodu. No i postępy nie są równe. Elektronika chińska już zaczyna być całkiem OK, ale samochody? Ale wspomniane silniki lotnicze (wielki problem w rozwoju chińskich sił zbrojnych)?
> Pomagały tej pozycji gigantyczne dotacje przekazywane przez agencje rzadowe i koncerny.
Bo tak to się robi. Tak to robią Japończycy, Koreańczycy czy Chińczycy.
IMHO: Myśmy też tak powinni robić. To najlepsza inwestycja w kraj.
> Również, drenaż mózgów z wszystkich stron świata.
To też prawda. Ale, znowu, te mózgi chcą być drenowane. Bez wyłożenia pieniędzy, zagwarantowania możliwości wygodnego życia (tu także kwestie braku opresji politycznych, czy światopoglądowych — konserwatystów strasznie złości wskazanie, że prawa dla LGBT przekładają się na innowacyjność gospodarki i sprzyjają by na drenażu mózgów zyskiwały społeczeństwa liberalne) nie byłoby to możliwe.
> Biegun magnetyczny nauki powoli przesuwa się na wschód.
Tak, Chiny, jak wcześniej Japonia i Korea zyskują. Jestem pod wrażeniem. Ale zmniejszanie dystansu do lidera, co najwyżej daje szanse na wyprzedzenie w przyszłości — nie stanowi opisu teraźniejszości. To po pierwsze.
Po drugie Chiny, Japonia, Korea, powiedzmy, że jeszcze Wietnamowi dobrze życzę — to ogromny potencjał ludnościowy. Gdy przeliczymy potencjał intelektualny na „głowę mieszkańca”, przewaga Zachodu jest tym większa. Być może Wschód osiągnie należną mu z powodów demograficznych pozycję. To jednak wciąż śpiewka przyszłości, a wyżej piszesz, że dominacja Zachodu to kwestia przeszłości.
> Zaczyna się zwykle od zrujnowania podstaw- poziomu szkół podstawowych.
Zauważyłbym, że parę państw robi całkiem niezłe szkolnictwo. Tu bardziej szkodzi sobkostwo elit, niż imigranci, o których piszesz.
> Ranking oparty na cytowaniach w uznanych ANGLOJĘZYCZNYCH pismach naukowych, recenzowany przez anglosaskich uczonych, anglosaskie redakcje?
1) Angielski jest obecnie międzynarodowym językiem nauki, jak kiedyś łacina. I w sumie dobrze, bo to praktyczne. Kiedyś musiałem przedzierać się przez wynalazek opisany po koreańsku — nawet z google translate to horror.
2) Redakcje są z całego świata, tu nie ma jakiegoś anglosaskiego spisku.
> Klub Białych nie przyjmuje kolorowych.
Jak najbardziej, jest ich tu całkiem sporo. Oczywiście, dyskutuje się o rasizmie i innych uprzedzeniach kulturowych (kalvarya01 tego nie lubi), ale to kwestia skali i ewentualnych preferencji by nie powstawały sitwy; a nie braku dopuszczania ludzi z zewnątrz. Tyle, że kryteria są merytoryczne…
@act
chyba troche za duzo slow ale na poczatek moze byc
a je sie to
z projektowaniem dzialan arytmetycznych w procesorach albo chipach fpga, cpld na bardzo fundamentalnym poziomie.
R.S. 20 CZERWCA 2022 15:21
Bias to bardzo ważny termin w probabilistyce i statystyce. W zasadzie nieodzowny i trudno coś powiedzieć żeby terminu nie użyć. Kiedyś przeglądałam polskie podręczniki do statystyki żeby się zaznajomić z polskim słownictwem, i pojawia się tam obciążenie. Estymator (nie)obciążony. A „bias-variance tradeoff” to „kompromis między obciążeniem a wariancją”. Pojawia się też stronniczość, ale chyba nie z tej bajki.
Z moich kontaktów z polskimi studentami (trochę ich ostatnio miewałam) widzę że oni już połowy terminów po polsku nie znają. Więc jeśli „bias” jeszcze nie jest słowem polskim, to niedługo będzie. Proponuję „bajas”.
R. S.
czy ‚Joseph Conrad’ ciagle stoi w Mystic Seaport?
Bylem tam 25 lat temu przez 2 tygodnie, chyba to Ty pisales o Connecticut?
just going off on a tangent 🙂
@R.S.
Czy chodzi ci o zapisywanie liczb ułamkowych w informatyce? Tam, gdzie się miejsce przecinka ustala arbitralnie w zależności, jak duże będą liczby całkowite?
Czy to się w ogóle jeszcze stosuje? Są w użyciu procesory bez jednostki zmiennoprzecinkowej (FPU)?
Bias przetłumaczony na niemiecki ma 144 znaczenia… O większości nie miałem dotąd pojęcia 🙁
@R.S.:
Widzę, że o podobnym zapisie mówi się, jako o kodowaniu z:
– przesunięciem;
– obciążeniem;
– spolaryzowanym.
Tak więc uderzałbym w przesunięcie lub obciążenie.
@markot:
A propos bez FPU — w szkole, na informatyce, dumny nauczyciel pokazywał nam, na poczciwym ośmiobitowcu bez jakiegokolwiek FPU, jak podnosić do potęgi stosując logarytmowane, mnożenie i funkcję wykładniczą. Podnosimy więc w Basicu 2^3 w ten sposób i wychodzi nam 7,99999…
PS.
Właśnie sobie to samo zrobiłem w Pythonie. No cóż…
act 20 CZERWCA 2022 14:06
sama widzisz…pogadalim. Trzymaj sie
Fajnie wiedzieć że jesteś gdzieś tam po drugiej stronie globu, podobnie myślisz i podobnej muzyki słuchasz. I nawet czytujesz podobne rzeczy. Czy już wiesz „What is real?” Trzymaj się też, bo dużo nas nie ma.
Co do gościa, jeśli rzeczywiście był „profesorem” uczelnianym, to tylko szkoda studentów. Bo zmarnowali czas kiedy mogli się czegoś sensownego nauczyć.
Albo się brzydko zestarzał, albo należy do grona tuzów polskiej nauki w rodzaju starego Giertycha i Zielińskiego antyszczepionkowca. I z takimi wybitnymi jednostkami Polska miała stać się drugą Irlandią, w co ciągle wierzy niejaki Sławczan, że gdyby nie Balcerowicz to Irlandią bylibyśmy i już.
Jeśli uznać to za pociechę, to poznawano się na geniuszu w porę i puszczano w dalszy obieg po innych naukowych „parafiach” 😉
Był uczelnianym adiunktem z doktoratem z Lema, wymęczonym w 30 lat po ukończeniu studiów. Opisywał kiedyś w necie swoje walki z UW o uznanie tego doktoratu, nie wiem, na czym się skończyło. Znany pieniacz (choć złagodniał i już mniej grozi sądem) i zamulacz blogów, co tutejszym Gospodarzom zdaje się nie za bardzo przeszkadzać. A jak już, to tną nie patrząc 🙁
Może wnosi element interesujący jakiegoś badacza?
Who knows…
markot 20 CZERWCA 2022 17:58
Doktorat z Lema super osiągnięcie, ale domniemywam że to nie było na polonistyce?
R.S. 20 CZERWCA 2022 15:21
Slope i bias to model liniowy jednowymiarowy. Nachylenie i przesunięcie jak najbardziej na miejscu.
Zapytałam google o bias i slope, powiedział „nachylenie i nachylenie”. Bądź tu mądry które jest które.
Mnie powiedziało „nachylenie i odchylenie”
Wartość rzeczywista = (nachylenie x liczba całkowita) + odchylenie
Doktorat z polityki (PhD in Politics) z podkreśleniem, że na Monash University w Melbourne, z podwójnym podkreśleniem: trzeci w Australii i 30. na świecie (w 2004)
A więc chapeau 😎
Kwalifikacji niezbędnych do zadręczania blogów „Polityki” ma aż nadto, ale dlaczego nie poszedł „w politykę”?
Zmarnowany talent 🙁
markot 20 czerwca 2022 18:26
” ale dlaczego nie poszedł „w politykę”?”
Jak to powiedział sp. gen. Petelicki – w Polsce do polityki pchają się miernoty niezdolne do zrobienia kariery gdziekolwiek indziej. Wychodzi na to, że nie musiał pchać się do polityki ….
Joseph Conrad, chyba wciąż jest. Strasznie dawno nie byłem w Mystic. Ostatni raz w akwarium z jakimś pociotkiem z Warszawy. W New London są łodzie podwodne, strach jechać, jeszcze ruszysci zbombardują .
Ostatni raz byłem w tamtych okolicach piętnaście lat temu.
Tuz obok w RI jest miejsce w Ft. Wetherill, Jamestown gdzie Gulf Stream wynosi rybki tropikalne.
https://loe.org/shows/segments.html?programID=18-P13-00035&segmentID=1
fajne miejsce można nurkować, rurka i maska tez wystarczy.
Mnie morza wystarczy tuz pod bokiem w Milford.
Zapraszam.
Jak wieje to deska na dach i za dziesięć minut jestem na plaży. Ale niestety kolana dają znać o sobie. Kiedyś przy 18-20mph dawałem godzinami rade pływać z żaglem 9.5m2 teraz już się trochę boję. . Mogę się popsuć.
…
Chyba najlepiej zostać przy bias albo bajas . Czasem trudno wykombinować o co chodzi z polskiej literatury. Slope to nachylenie tu problemu nie ma.
Obliczenia stało-przecinkowe są bardzo szybkie, albo trzeba modelować cały algorytm, aby unikać błędów.
Często operując liczbami rzeczywistymi nie zdajemy sobie sprawy jak skomplikowane są operacje na poziomie bajtów.
A tu masz dochodzą komputery kwantowe.
Mój przyjaciel, mówi ze on studentów tego uczyć nie będzie, bo zanim komputery kwantowe pojawia się w sprzedaży w Wal-Marcie czyli takiej „Biedronce” to on już będzie na emeryturze.
Orteq 20 CZERWCA 2022 13:44
Zgoda, ale wytłumacz to np. takiemu PAK4. który ma umysł tak wyprany przez jankeską propagnde i jest przy tym tak tępy z natury, że nie jest on w stanie samodzielnie myśleć.
Pozdrawiam,
LK
act 20 CZERWCA 2022 14:25
Sam o sobie napisałeś pełną prawdę, ze niejaki act, znany psycho-troll rozwalił kolejny blog swymi chamskimi atakami ad personam. 🙁
wiesiek59 20 CZERWCA 2022 15:38
Racja!
izabella 20 CZERWCA 2022 17:26
Skąd wiesz co wykładałem i jak wykładałem? Jakie ty masz kwalifikacje, aby mnie oceniać i to publicznie, na dodatek tchórzliwie ukrywając się pod nickiem?
markot 20 CZERWCA 2022 17:58
Na Monash byłem początkowo uczelnianym adiunktem (lecturer) z doktoratem z Lema, uzyskanym po 4 latach bycia doktorantem, ale na studia wróciłem dopiero w roku 1993, studiując najpierw ekonomię na The University of Melbourne w latach 1993-1996 (MA by Thesis), po czym byłem doktorantem na Monash University w latach 1996-2002 (PhD). Następnie bylem profesorem na różnych uczelniach, w takich państwach jak Cypr, Portugalia i Polska. Jesli więc coś piszesz, to pisz prawdę, gdyż kłamstwa mają, jak wiadomo, bardzo krótkie nogi. I ciekaw jestem, czy ty byłbyś w stanie uzyskać jakikolwiek doktorat na Monash University…
izabella 20 CZERWCA 2022 18:12
To było na Wydziale Nauk Politycznych Monash University w Melbourne, a tytuł to „Visions of the Future in the Writings of Stanisław Lem” („Wizje przyszłości w twórczości Stanisława Lema”) wydane w Saarbrücken przez Lap Lambert Academic Publishing w roku 2010 (https://www.academia.edu/42852125/VISIONS_OF_THE_FUTURE_IN_THE_WRITINGS_OF_STANISŁAW_LEM_Vol_I). A ty masz PhD z jakiej dyscypliny naukowej i z której uczelni?
markot b20 CZERWCA 2022 18:26
Ale bardziej jestem dumny z MA by Thesis z ekonomii – The University of Melbourne:
University rankings:
QS World 37
THE World 32
ARWU World 33
Australian rankings
QS National 2
THE National 1
ARWU National 1
Tytuł rozprawy: „Decline of Manufacturing Industry in Poland 1990-1996”.
R.S. 20 CZERWCA 2022 19:28
Obawiam się, że komputery kwantowe to jest coś takiego jak obiecywana od lat 1950-tych tania energia z reakcji syntezy jądrowej. :-(
Wiem gdzie jest East London, ale New London?
Bias in statistics: systematic distortion of a statistical result due to a factor not allowed for in its derivation (systematyczne zniekształcanie wyniku statystycznego z powodu czynnika, który nie został uwzględniony w jego uzyskaniu).
Po polsku „bias” to jst więc stronniczość, brak obiektywiuzmu etc.
act 20 CZERWCA 2022 15:57
Politechnika Poznańska:
Webometrics ranked it at no. 842 in the World.
W zestawieniu najlepszych uczelni świata – QS World University Ranking – PP utrzymuje stabilną pozycję w przedziale 801-1000.
1493 miejsce na świecie według listy Center for World University Rankings na lata 2020-21.
1750 miejsce wśród uczelni na całym świecie w UniRank Top Universities.
kalvarya01,
I co z tego? Znalazlem w guglu i zacytowalem.
W Poznaniu bylem raz jako dziecko – w operze na ‚Strasznym Dworze’.
izabella 17:26,
coraz mniej wiem ‚What is real’ – ksiazka jednak jest b. dobrym wprowadzeniem do tematu q. ph.
Polecam Philipa Goff’a ‚Galileo’ s error’.
Goff swietnie pokazuje, czego fizyka nawet nie potrafi dotknac. Do panpsychizmu jednak ani on, ani Chalmers i wielu innych mnie nie przekonaja.
‚The hard problem in philosophy’ pozostaje jak na razie (a moze i na zawsze) nieruszony.
PAK4 20 CZERWCA 2022 16:01
1. Czy rankingi takie jak np. THE czy QS też są według ciebie chińskie? Otwórz lodówkę, a Chińczyk z niej wyskoczy. ;-)
2. W wielu dziedzinach dominują dziś Chiny a Rosja ma silną pozycję w badaniach kosmosu, aeronautce czy w produkcji nowoczesnej broni. I czy naprawdę sądzisz, że chińskie samoloty maja złe silniki?
3. Japonia i Korea nie naśladują Zachodu, ale mają one swoje własne modele rozwoju, zupełnie inne wartości, inną filozofię, w tym polityczną etc niż tzw. Zachód. Czy ty kiedyś byleś w Japonii? Bo ja – tak….
4. Tak, ale w USA to jest wbrew tamtejszej oficjalnej ideologii i wbrew oficjalnej reżimowej doktrynie wolnego rynku i braku etatyzmu.
5. Ale nam tak NIE wolno robić od roku 1989.
6. NIE, te mózgi NIE chcą być drenowane, ale po prostu nie mają innego wyjścia. Opresje polityczne i światopoglądowe są zaś dziś powszechne na tzw. Zachodzie, a prawa dla LGBT wcale NIE przekładają się na innowacyjność gospodarki. To jest fałszywa korelacja, czyli spurious correlation, tak jak np. korelacja sprzedaży lodówek i pralek. Znów wychodzi u ciebie brak ścisłego wykształcenia.:-(
7. Naturalne jest, że najludniejsze państwa świata z najstarszymi i nieprzerwanie istniejącymi kulturami, czyli Chiny i India, będą znów dominować nad gospodarką świata, tak jak było to jeszcze na początku XIX wieku.
8. Nie ma już przewagi Zachodu – są tylko jego ostatnie podrygi… Chiny już dziś maja realną gospodarkę większą niż USA, ale o czym się nie mówi na tzw. Zachodzie. A zrujnowanie podstaw, czyli poziomu szkół podstawowych, to jest dziś polska rzeczywistość. Podobnie jak zapaść nauki i szkół wyższych. :-(
9. Angielski też utraci swoją pozycję, tak jak utraciły ją greka, łacina, francuski czy niemiecki. Redakcje są zaś z całego świata, ale na Zachodzie liczą się dziś wciąż tylko pisma anglojęzyczne.
10. Tak, ja bardzo nie lubię rasizmu. A kryteria merytoryczne już od dawna zostały na tzw. Zachodzie zastąpione „genderowymi”. Und da liegt der Hund begraben. :-(
Dobranoc! 🙂
act 20 CZERWCA 2022 22:27
A ja byłem w nim kilka dni temu, choć tylko przejazdem, 😉
I czy znasz tę książkę o Poznaniu: MACIEJ PŁAZA – O POZNANIU W TWÓRCZOŚCI STANISŁAWA LEMA?
niestety nie, zanotuje
czytalem Lema i o nim od 13 roku zycia, wywiad rzeke tez.
act 20 CZERWCA 2022 23:25
Sam Bereś przyznaje, że Lem opowiadał mu bajki (niekoniecznie robotów) zamiast prawdy… 🙁
Pa!
Dekada Edwarda Gierka pokazała, że do wszystkiego należy podchodzić cierpliwie z rozwagą i pamiętać o porzekadle „dobry zwyczaj nie pożyczaj”.
Nie znam kwoty dzisiejszego zadłużenia, ale jakiekolwiek by była, trzeba będzie to latami spłacać, chyba że jakiś kataklizm nas ogarnie, a tego byśmy nie chcieli.
Sygnalizują tu i ówdzie wysokie podwyżki za ogrzewanie, ale pokazują też puste place na których były składowane węgiel i miał węglowy, zatem kończy się ciepła woda w kranie i wracamy do punktu wyjścia.
Trzeba się przygotować na trudną zimę. Dzisiaj rąbałem drewno na opał, a właściwie chrust z ogrodu. Zmniejszam koszty i poprawiam kondycję fizyczną. Może się przydać
Gospodarzu Szanowny,
Niedowiary. Szarańcza ruso-faszystów oraz antysemitów przejęła stery pańskiego wehikułu, co Panu najwyraźniej nie przeszkadza.
Usuwanie z innych blogów towarzycho psycholi, udziela się tu wyłącznie w celach propagandowej biegunki o morderczo-złodziejskim Zachodzie, banderowskiej Ukrainie oraz o wspaniałej matuszce Rassiji. Tematyka proponowana przez Gospodarza jest olewana, służy wyłącznie jako pretekst do siania lewizny. A szkoda – pamiętam lepsze chwile oraz wysokich lotów wpisy.
@kalvarya
Nie podniecaj się tak rankingami. I tak nie widać chętnych na ściganie się z tobą na „profesorstwo” w podrzędnych uczelniach. Takiemu geniuszowi wszechnauk mało kto w świecie dorówna 🙄
Równowaga nastanie, gdy jakiś Australijczyk przyjedzie do Polski doktoryzować się z australijskiej literatury sci-fi albo polityki wobec środowiska np. „Czy misie koala w Południowowschodniej A. wyginą do 2050 roku?”
No i nadal nie wiem, jak w końcu poszło na tym UW (pozycja 401-500) z uznaniem doktoratu z byłej pierwszej trzydziestki (ale Political Sciences zaledwie 151-200) 🙁
@ls42
Ja dziś wymieniłem czereśnie na ryby złowione rano przez sąsiada. Transakcja ku obopólnemu zadowoleniu, chociaż moje było chyba większe, bo nie dosyć, że złowił i oprawił ryby, to i czereśni sam sobie narwał 😎
wciskanie kitu trwa
Adjunct and conjoint professor are honorary titles bestowed upon a person to formally recognise that person’s non-employment ‚special relationship’ with the university
podkreslenie non-employment
adjuncts w uniwersytetach amerykanskich, sluza do zapychania dziur i niestety zatrudnianie ich na „chwile” jest czystym swinstwem w stosunku do studentow.
W polskim sytemie akademickim adjunkt mial inny status – znacznie wyzszy.
Jak sie chce komentowac na temat komputerow kwantowych, albo arytmetyki staloprzecinkowej albo swiec samochodowych to trzeba sie choc troche znac na temacie.
Lemin sie w grobie przewraca ze wstydu.
Pozostało pchanie się na blogi. Ale dlaczego miernoty w polityce miałyby mu przeszkadzać? Tym bardziej mógłby zabłysnąć.
@act
20 czerwca 2022
23:23
Koniecznie zanotuj, tylko nie samymi wielkimi literami 😀
Powyższe jest odpowiedzią na komentarz @kaesjota 18:44
Może niepotrzebna złośliwość ale trudno się powstrzymać kiedy szarlatan śmie wypowiadać się obraźliwie o umysłach o niebo solidniejszych od tego, który sam posiada.
markot
21 CZERWCA 2022
1:47
🙂
Jako polski odpowiednik słowa “bias” w statystyce proponuję “skrzywienie”. Błędy = skrzywienia w procedurze badania statystycznego mniej lub bardziej zniekształcają jego wynik.
Napisawszy to zajrzałam jeszcze do słownika polskiego i trafiłam na “skrzywienie poznawcze”, odpowiednik “cognitive bias”.
@ls42:
Rozwaga rozwagą, ale spotkałem w publikacjach zachodnich, że to wówczas dość powszechny, a nie tylko gierkowski problem był — rozpocząć inwestycje za pożyczone pieniądze, tuż przed kryzysem naftowym i stagflacją, oraz z wynikającymi z nich problemami z popytem. Gierkowi można wyrzucać raczej, że część tych pieniędzy była katastrofalnie źle zainwestowana.
Choć, swoją drogą, jako świat chyba próbujemy powtórzyć ten scenariusz (stagflacja), więc trzeba zapiąć pasy…
@kalvarya01:
> Czy rankingi takie jak np. THE czy QS też są według ciebie chińskie?
Muszę sprawdzić czyje. Uchwyciłem się tego, który dawał średnie wyniki z podrzuconych przez Ciebie. Zresztą do dalszej tezy, to zupełnie wystarczający argument był.>
> aeuronautyka
Nie na wszystkim się znam, więc dopiero tu się włączam. Ile szanowny zna konstrukcji cywilnych samolotów pasażerskich z Chin czy Rosji używanych na świecie? Oba państwa próbują, w mniejszych lub większych bólach. Ale przebić się im ciężej niż Brazylii.
> czy w produkcji nowoczesnej broni.
Chiny dopiero teraz dołączają do czołówki — jeszcze nie tak dawno odstawały in minus od Rosji, a ta nadal odstaje od Zachodu.
> I czy naprawdę sądzisz, że chińskie samoloty maja złe silniki?
Nie.
Albo kupowali w USA (mieli 100 sztuk, samoloty zrobili dwusilnikowe, więc mogli zrobić góra kilkadziesiąt sztuk; odgrażali się, że wyprodukują własne, ale im nie wyszło).
Albo kupowali w Rosji, która ma gorsze silniki niż USA, czy Francja, ale i tak lepsze niż reszta świata.
Własne silniki chińskie były na poziomie technologicznym lat 60-tych. I to początku tej dekady.
> Japonia i Korea nie naśladują Zachodu, ale mają one swoje własne modele rozwoju, zupełnie inne wartości, inną filozofię, w tym polityczną etc niż tzw. Zachód.
Jakoś dziwnym trafem wprowadziły parlamentarną demokrację, z wielu partiami…
> Ale nam tak NIE wolno robić od roku 1989.
Ależ wolno. Nie myl niechęci polityków (a przypominam — gdzieś połowa „młodych” polityków PO, czy PiS przeszła do tych partii po stażu o leseferystycznego i flirtującego z nacjonalistami Korwina), z niemożnością.
BTW. Byłem kiedyś na spotkaniu z niemieckimi zarządzającymi nauką. No i opowiadają jak zdobywają pieniądze z UE, tak niezupełnie zgodnie z przeznaczeniem (z koszyka na nauki stosowane brali na nauki podstawowe). Ktoś ich pyta: jak to robicie? A oni: lobbujemy! I wam też radzimy!
I to była rada z dobrego serca. No, ale żeby lobbować to trzeba umieć obracać się po salonach, a nie że były minister s.z. publikuje mema z miniaturkami przywódców unijnych…
No i w naszym rankingu wartości politycznych, grill na działce jest wyżej niż wszystkie uniwersytety razem wzięte.
> Naturalne jest, że najludniejsze państwa świata z najstarszymi i nieprzerwanie istniejącymi kulturami, czyli Chiny i India, będą znów dominować nad gospodarką świata, tak jak było to jeszcze na początku XIX wieku.
Po pierwsze, jak widziałem kiedyś zestawienia to raczej XVIII. Chiny zaliczyły wówczas wielki kryzys cywilizacyjno-polityczny.
Po drugie, co to znaczy „dominować”. Bo że Chiny może się zbliżą do produkcji Zachodu na głowę mieszkańca, to ja się zgadzam. Ale czy wyprzedzą? Gonienie kogoś kto wciąż robi postępy nie jest takie proste.
Po trzecie, Chiny już wpadają w pychę i zadufanie. To im bardzo źle wróży. Wisi też nad nimi problem demograficzny. Tak, że Chiny też powinny zapiąć pasy.
> Angielski też utraci swoją pozycję, tak jak utraciły ją greka, łacina, francuski czy niemiecki. Redakcje są zaś z całego świata, ale na Zachodzie liczą się dziś wciąż tylko pisma anglojęzyczne.
Jakiś inny język, który się liczy? Cały Daleki Wschód publikuje po angielsku.
Bądźże pozdrowiony ze Swoim Genderem i uprzedzeniami!
Ukraina i Gruzja stalinowska okupowały kraj nad Wisłą jako ZSRR … tak sugerują hunwejbini nad Wisłą … Tak sobie myślę prywatnie … teraz ZSRR staje się okupantem sierotą … jedynym odpowiedzialnym za ciemność tego okresu .. i gwałty …
Lapidarne rządy w Israelu … liczba 447 wróci nad Wisłę jak zły szeląg … Tak sobie myślę prywatnie … liczmy się jak … wraca …
To Kaczyński decyduje kiedy jest w rządzie a kiedy nie jest … Tak sobie myślę prywatnie … rodzi się nowa pisowska demokracja … kaczyzm … a czepiają się Kimów …
ls42 20 CZERWCA 2022 23:33
Dług Gierka w roku 1980: 24 mld USD
Dług Balcrowicza i ski w roku 2022: 366 mld USD
(Wedłog https://tradingeconomics.com)
PAK4 21 CZERWCA 2022 5:49
To nie było tak, że część tych pieniędzy była katastrofalnie źle zainwestowana, choć oczywiście, jak to zawsze i wszędzie, trafiały się nietrafione inwestycje albo źle zarządzane, ale problem było to, że Zachód przestał od nas kupować, ale wymagał od nas spłaty lichwiarskich odsetek, a Gierek chciał je mimo to spłacać, podobnie jak Ceauşescu. Na szczęście dla Gierka, odsunięto go jednak od władzy…
Redes22 21 CZERWCA 2022 3:45
Jako polski odpowiednik słowa “bias” w statystyce nie może być słowo “skrzywienie”, gdyż “skrzywienie” w statystyce matematycznej odnosi sie do rozkładu, w którym nie występuje symetria, a krzywa rozkładu pokazuje „ogon” po lewej lub prawej stronie. Jest on znany jako rozkład skośny albo skrzywiony, a więc skośność (skrzywienie) jest asymetrią występującą na krzywej lub histogramie poza krzywą symetryczną lub normalną.
Odejście Kaczyńskiego … Tak sobie myślę prywatnie … to takie przełożenie pilota z ręki do ręki …
markot 21 CZERWCA 2022
Jeśli dla ciebie Monash University jest podrzędną uczelnią, to o czym tu mamy mówić? Poza tym, to Lem to jest „coś” znacznie więcej niż sci-fi czyli tzw. „pulp” SF made in USA, a problem z koalami wymaga znacznie więcej niż napisanie rozprawy na stopień doktora czy nawet PhD. A co do nostryfikacji, to mi jej w Polsce odmówiono, ale uznano mój PhD z Monash w Portugalii, gdzie nawet uznano go oficjalnie za odpowiednik tamtejszej habilitacji.
Redes22 21 CZERWCA 2022 1:35
Miernoty wszędzie nie dopuszczają lepszych od siebie. I dlatego też Zachód skazany jest na klęskę w konfrontacji ze Wschodem, gdzie stosowane są racjonalne, merytoryczne kryteria, a nie „genderowe”.
PAK4 21 CZERWCA 2022 6:02
1. Jaka widzisz, uprawiasz tzw. jumping to conclusion – jumping to conclusions (officially the jumping conclusion bias, often abbreviated as JTC, and also referred to as the inference-observation confusion) is a psychological term referring to a communication obstacle where one “judge[s] or decide[s] something without having all the facts; to reach unwarranted conclusions”.
2. Brazylia ma dostęp do rynków na tzw. Zachodzie, który blokuje się dla Rosji i Chin, chyba, że wierzysz w tzw. wolny handel…
3. Skąd wiesz, że Chiny odstają w czymkolwiek od tzw. Zachodu? Może w ilości mieszkańców slumsów…
4. Powtarzasz bajki, rozpowszechniane przez samych Chińczyków w celu zmylenia tzw. Zachodu. Słyszałeś też może o „reverse engineering”?
5. Gdzie ty masz na świecie demokrację? Mylisz jej pozory z rzeczywistym ludowładztwem, którego jednak nigdzie juz na świecie nie znajdziesz.
6. Nie, nie wolno. KE tego zabrania pod pozorem prowadzenia polityki wolnorynkowej, która nie pozwala na to, aby państwo finansowało tzw. infant industries, szczególnie w domenie tzw. hig tech. Używam, z braku czasu, terminów anglojęzycznych, ale ogólnie znanych. A lobbowanie to jest po prostu przekupywanie i korumpowanie, a więc nie rozumiem, dlaczego się tym tak zachwycasz…
7. Poszukaj w Sieci publikacji Maddisona na temat historycznych statystyk ekonomicznych. Np. tu: https://www.rug.nl/ggdc/historicaldevelopment/maddison/?lang=en
Poza tym, to tzw. Zachód wpadł w pułapkę stagnacji, genderyzmu, chowu wsobnego elit etc. a Chiny oczywiście mają swoje problemy, ale akurat problemu demograficznego to u nich nie ma, gdyż problemem ludzkości numer jeden jest obecnie i w przewidywalnej przyszłości nadmiar ludności, a nie jej brak.
8. Przyszłość ma język mandaryński, a to źle wróży Europie, USA, Kanadzie, Australii etc. etc.
Ukłony na wzór japoński. 😉
Rozpad każdego imperium jest niedostrzegalny dla żyjących w tym czasie świadków.
Trwa kilka pokoleń- na ogół.
Choć zdaje się mamy pecha, bo rozkład anglosaskiego przyspieszył niesamowicie.
Nikt nie przewidział upadku imperium hiszpańskiego, francuskiego, brytyjskiego, czy rosyjskiego, a jednak stało się to faktem.
„Brzemię białego człowieka” po 150 latach stało się chyba zbyt ciażącym ciężarem.
Utrata przewagi militarnej, technologicznej, handlowej, finansowej to kres.
Pozostała jedynie przewaga propagandowa.
A co do nauki.
Nanotechnologia, przemysł kosmiczny, biotechnologie, rozwój SI, atomistyka.
Tu rozstrzygnie się moim zdaniem walka o prymat.
Wymaga to nakładów finansowych, zasobów naturalnych, energii i tzw.
„kapitału ludzkiego”.
Oraz koordynacji ze strony państwa.
Dla zachodu ze swoja indywidualistyczną koncepcją życia jest to nieosiągane.
Dla wschodu, z kolektywistycznym sposobem działania, merytokracją, wykonalne.
Jeszcze pamiętam z czasów dzieciństwa ( lata 60-te ) , gdy funkcjonowało w obiegu określenie – „japońska tandeta” lecz 20 lat później określenie ” japoński wyrób” stało się synonimem najwyższej jakości.
W okresie II WŚ i po niej mocno rozwinęła się ( szczególnie w USA ) nauka w zakresie organizacji zarządzania, racjonalizacji produkcji. Jednak wojenna i powojenna hossa dla gospodarki USA sprawiła, że amerykańscy przemysłowcy nie byli tymi innowacjami zainteresowani natomiast „kupili” to Japończycy. Zaprosili do siebie amerykańskich uczonych, którzy nie znaleźli posłuchu u siebie i przekładając ich teorie w praktykę zaczęli je stosować w swoich fabrykach.
W proces racjonalizacji produkcji, ulepszania produktu angażowali także szeregowych pracowników ( słynne japońskie Kółka Jakości ) gdyż uznali, że do usprawniania pracy najlepiej nadają się ci, którzy na co dzień ją wykonują.
Może Japończycy nie mieli w swych dorobku wielu wybitnych odkryć naukowych lecz byli bardzo dobrymi ich WYKONAWCAMI. A pomysły z początku kradli a później kupowali licencje i je doskonalili.
To funkcjonuje nadal. Kilka lat temu byłem w poznańskim zakładzie Bridgestone i na tablicy ogłoszeń czytam apel Kółka Jakości – ” Pomyśl, jak POZBAWIĆ swego kolegę pracy”. Zwróciłem na to uwagę jej pracownikowi mówiąc, ze chyba chodziło o to, by koledze ULŻYĆ w pracy. Przy następnej wizycie już tego nie było.
U nas w czasach PRL-u działały kluby racjonalizatorów i ten ruch mocno propagowano lecz było to działanie bardziej propagandowe niż praktyczne.
Wg przepisów autorowi pomysłu należało się dodatkowe wynagrodzenie, proporcjonalne do korzyści wskutek jego wdrożenia. Problem był w tym „wdrożeniu”. Gdy w grę wchodziła „duża kasa” to bez dopisania szefów jako współautorów pomysłu szans na jego wdrożenie nie było.
Mimo , że od upadku PRL-u minęło ponad 30 lat reguła ta obowiązuje nadal.
I pod tym względem nie dorównamy krajom azjatyckim, w których interes społeczności przedkłada się nad interes jednostki.
@kalvarya01 – 20 CZERWCA 2022 – 21:10
„Orteq 20 CZERWCA 2022 13:44
Zgoda, ale wytłumacz to np. takiemu PAK4. który ma umysł tak wyprany przez jankeską propagnde i jest przy tym tak tępy z natury, że nie jest on w stanie samodzielnie myśleć.”
Jankeska propaganda dzisiaj jest pod wpływem neokonow, którzy narzucili Bidenowi, oraz światu, najpierw politykę a następnie narracje antyrosyjska. Taka przypadłość.
https://www.dailysabah.com/opinion/columns/the-west-finally-unplugged-russia-from-the-world
Rzecza najdziwniejsza w nowej światowej sytuacji jest również i Polska uległość tej niecodzienności wielkoświatowej. Rozchodzi się o słynną kacza zapyziałość polska. Te, którą miała nas uchronić przed przed zbyt namolna amerykanizacja.
Bo reszta europejskiego Zachodu się poddała bez bicia. No, może z wyjątkiem Węgier Orbana. A tu raptem mamy również i polski wyścig po względy tych, którzy narzucili zachodowi nowa antyrosyjskość. Najpierw wepchnąwszy Rosję w wojnę na Ukrainie, po wyprodukowaniu kijowskiego Majdanu w 2014 roku.
https://canadiandimension.com/articles/view/the-hidden-origin-of-the-escalating-ukraine-russia-conflict
Wczesne samochody elektryczne przewyższały konkurentów na benzynę, a ludzie je lubili, ponieważ nie miały zapachu, hałasu ani wibracji samochodów benzynowych, były łatwiejsze w obsłudze i nie wymagały rozruchu ani zmiany biegów. NYT zauważył, że kobiety szczególnie preferują je ze względu na brak dymu i śmierdzących oparów, zwłaszcza podczas tankowania.[ 1 ] [ 2 ] Wydawało się pewne, że pojazdy elektryczne są falą przyszłości, ale potem w ciągu zaledwie trzech lat transport krajobraz zmienił się nieodwracalnie, a pojazdy elektryczne, podobnie jak dinozaury, doznały śmiertelnej zmiany klimatu i zmarły.
https://www.bluemoonofshanghai.com/politics/7243/
===========
Kawałek historii…..
Nigdy nie zwycięży najlepsze rozwiązanie.
Zawsze, najdroższe.
Orteq
21 CZERWCA 2022
12:34
Jak tam wasz mały faszysta- Trudeau?
Tu i ówdzie psioczą na niego kanadyjscy uczestnicy dyskusji.
Totalitaryzm niejedno ma imię, ale jedno źródło.
@kalvarya01:
> Jaka widzisz, uprawiasz tzw. jumping to conclusion
Jak widzisz uprawiasz zakłamaną propagandę.
a) Powołujesz się na trzy rankingi uniwersyteckie.
b) Sprawdzam jeden (z ograniczeń czasowych) — ten, który wypadł przeciętnie dla Uniwersytetu Moskiewskiego.
c) Cytuję dane, które wskazują jak słabo wypada nauka rosyjska na tle Zachodu.
d) Na co mam kontrę ze strony Wieśka, że to zachodnia manipulacja.
e) Na co odpowiadam, że to ranking chiński.
A Ty mi wyskakujesz z JTC. Lepiej odpowiedz na pytanie początkowe — dlaczego ci wszyscy straszący Zachodem, upadkiem jego cywilizacji itp. politycy, myśliciele i publicyści nie wysyłają swoich dzieci na Uniwersytet Moskiewski, czy na naukę do Chin, ale celują w Camrbdige i Oxfordy? Dlaczego Putin nie załatwia swojej córce daczy na Uralu, ale we Francji? Albo Miediediew, dlaczego patronuje karierze syna w USA a nie Chinach, czy — niech będzie, że mandaryński to przeszkoda — w Kazachstanie? Bo widzisz, ja tu dostrzegam zakłamanie, takie jak u krewnej biskupa na aborcji, co to „sytuacja jest niestandardowa”.
> Brazylia ma dostęp do rynków na tzw. Zachodzie, który blokuje się dla Rosji i Chin, chyba, że wierzysz w tzw. wolny handel…
Od paru lat jestem poza tematem (ogródek i w ogóle), ale jeszcze nie tak dawno śledziłem hobbystycznie co się dzieje na rynku lotniczym. I Rosja miała swoją chwilę na sprzedaż za granicą — to katastrofa podczas pokazów podcięła im skrzydła; a potem przyszły wyniki awaryjności i horrendalne koszty serwisu. Chiny też mają szansę, podkradając technologie airbusa. To nie jest spisek wrogiego rynku — to jest trudność z wejściem na rynek dla niedoświadczonych i mało kompetentnych „nowicjuszy”. Oczywiście wiem, że Rosja robiła samoloty pasażerskie, ale technologicznie została w tyle za Zachodem (nawet swojego eksportowego Su próbowała robić z udziałem zachodniego przemysłu by nadrobić braki).
> Skąd wiesz, że Chiny odstają w czymkolwiek od tzw. Zachodu? Może w ilości mieszkańców slumsów…
Jak pisałem wyżej — śledziłem doniesienia z zakresu lotnictwa. Widzę też, jakie opinie mają chińskie samochody — bo Chiny próbują, drogą Japonii i Korei, wchodzić na rynek europejski. I nie są blokowane urzędowo. Po prostu produkują badziew. Próby zrobienia czegoś „na poziomie” oznaczają zaś brak konkurencji cenowej, bo jako-taka produkcja chińska co do jakości jakoś nagle traci swoje atuty w tym zakresie.
> Powtarzasz bajki, rozpowszechniane przez samych Chińczyków w celu zmylenia tzw. Zachodu. Słyszałeś też może o „reverse engineering”?
Oczywiście. I to widać — Chiny korzystają z nauki, jaką wyciągają z bycia „składaczem” elektroniki użytkowej. Przeszły od składania do własnych projektów, może nie najlepszych na świecie, ale jednak na poziomie.
Chiński projekt samolotu pasażerskiego to też odprysk wcześniejszego doproszenia się o możliwość składania. Zobaczymy jak im pójdzie.
Problem polega na tym, że w Chinach montowano niektóre dobra konsumpcyjne; a takie silniki lotnicze to inna para kaloszy. Dość wyrafinowana technologia (materiały na sprężarki itp.), którą niewielu posiada, i którą nikt nie chce się dzielić. (Np. Rosja nie chce, a Chiny by jej technologię, tu bardziej zaawansowaną, chętnie przejęły.)
> Gdzie ty masz na świecie demokrację? Mylisz jej pozory z rzeczywistym ludowładztwem, którego jednak nigdzie juz na świecie nie znajdziesz.
Pan Ultrakonserwatysta w swoim sosie, wszystko źle, czekać na wieczne nigdy i narzekać na nowoczesność. Puk, puk, XVIII wiek się skończył jakąś chwilę temu.
> Nie, nie wolno. KE tego zabrania pod pozorem prowadzenia polityki wolnorynkowej, która nie pozwala na to, aby państwo finansowało tzw. infant industries, szczególnie w domenie tzw. hig tech.
UE, Polska mniej, całkiem sporo przeznacza na to pieniędzy. Wiem z dobrego źródła, by nie powiedzieć z pierwszej ręki 😉 więc nie próbuj mi wmawiać propagandowych kłamstw.
> A lobbowanie to jest po prostu przekupywanie i korumpowanie
Czytałeś ustawę o lobbingu, by wiedzieć jak się go definiuje?
> Poza tym, to tzw. Zachód wpadł w pułapkę stagnacji, genderyzmu, chowu wsobnego elit etc.
Siłą Zachodu była różnorodność i zdolność do adaptacji, wynikająca z demokracji, wolnego rynku itp. Czy Chiny będą miały podobną siłę? Nie wiem.
> Chiny oczywiście mają swoje problemy, ale akurat problemu demograficznego to u nich nie ma
Słyszałeś o polityce jednego dziecka? Przemyślałeś, jak to będzie wyglądało, gdy to pokolenie jedynaków się postarzeje?
Cytat . Czy jakiś posiadacz doktoratu z chmur mógłby wyjaśnić dlaczego został zamieszczony a nie zacytowany ?
Posiadacze doktoratów wszystkich krajów świata , łączcie się ( google podpowiada – leczcie sie ) w tłumaczeniu , dlaczego .
…………..
„Łódź. Chmura rolkowa na niebie. Jak się tworzy?
– To jest kondensacja unoszącego się ciepłego powietrza. Jest ono zaciągane znad powierzchni ziemi, a następnie dociera do warstwy, która go nie przepuszcza. W ten sposób tworzy się chmura rolkowa. Utrzymuje się ona do momentu, aż to ciepło przestanie się gromadzić. A potem zniknie – tłumaczy nam Turała. ”
Ps.
Jeżeli ryby były z Neru to ten co wziął czereśnie zrobił lepszy interes
Dlaczego nazwy rzek są takie dziwne ? Ner, Bzura , Warta , Odra , Wda ..
@olborski:
Bo często są stare. Starsze od Polski.
Michael Hudson 1:21:43
Europa popełniła ekonomiczne samobójstwo, Stany Zjednoczone zaoferowały swoim przywódcom dużo pieniędzy na kontach offshore i zapewniły ich dzieciom bezpłatną edukację w Stanach Zjednoczonych. Ale w zamian musieliby reprezentować Stany Zjednoczone, a nie Niemcy, Francję czy inne kraje. Amerykanie od lat mieszają się w politykę europejską. Politycy europejscy nie reprezentują swoich krajów. Reprezentują amerykański Departament Stanu i amerykańską dyplomację. I powiedziano im, aby zamknęli swoje kraje w gospodarce USA.
https://thesaker.is/economic-rent-and-exploitation-michael-hudson-shepheard-walwyn/
===========
Proste jak budowa cepa.
@olborski
Ryby (łososiowate) z rodzaju coregonus, prawdopodobnie sielawy, były z jeziora fiordowego, głębokiego na 217 m, czystego i chłodnego.
W smaku zupełnie różne od czereśni.
Stratocumulus volutus (ew. altocumulus v.) to piękne zjawisko, nie wróżące nic dobrego 🙁 Chmura rolkowa brzmi jakoś niepoważnie, bo to bardziej walec albo długa rura
Brytyjski szef wojskowy Sztabu Generalnego właśnie objął to stanowisko i powiedział już armii, że muszą przygotować się do wojny z Rosją w Europie. Kazał każdemu żołnierzowi przygotować się do walki z Rosją w potencjalnej III wojnie światowej. Zobowiązał się stworzyć armię, która może pokonać Rosję w bitwie i powiedział, że musimy teraz przygotować się „do ponownej walki w Europie”. Dodał w czwartym dniu pracy: „Teraz palący imperatyw wykucia armii zdolnej do walki u boku naszych sojuszników i pokonania Rosji w bitwie”.
https://www.armstrongeconomics.com/world-news/war/britain-head-of-military-tells-troops-prepare-for-wwiii/
=======
Hmm…..
Armia brytyjska liczy 76 000 ludzi….
@wiesiek – 12:40
Trudeau MUSI popierać wielkiego sąsiada bo takie sa impoderabilia. A w jakiej jest aktualnie sytuacji to tu sobie niektórzy pozwoli pospekulować
https://www.ctvnews.ca/politics/don-martin-the-fall-of-justin-trudeau-has-begun-1.5946788
Mozna to skomentować, niezbyt odkrywczo, klasykiem:
„wiadomość o mojej śmierci jest nieco przesadzona”
Putin powinien dążyć do samostanowienia narodów zdeptanych brytyjskim butem … Tak sobie myślę prywatnie … to ciekawsze zajęcie … przywrócić podbitym terytoriom świata wolność … czas skończyć z hipokryzją obrońców banderowskiej Ukrainy z rusofobicznych pobudek … kto bez grzechu …
@SŁOWIANIN STANISŁAW:
Wiesz, brytyjski but daleko. Za to rosyjski blisko. Nie mógłby Putin zacząć od dążenia do samostanowienia narodów zdeptanych rosyjskim butem?
Dlaczego świat ma tolerować brytyjskie ludobójstwo suwerennych narodów świata … Tak sobie myślę prywatnie … z korony brytyjskiej królowej kapie krew kolonialnych ofiar … a szukają krwi w rosyjskiej ropie i gazie …
Hej, PAK-u-po4ny
Potrafiłbyś powymieniać te narody zdeptane rosyjskim butem? Wojennym, w szczególności?
Niektórzy głosili, ze podbojowość Rosji w porównaniu z PANOWANIEM USA w dzisiejszym świecie, to pikuś nie zasługujący nawet na przymiotnik malutki
https://www.newyorker.com/news/q-and-a/why-john-mearsheimer-blames-the-us-for-the-crisis-in-ukraine
@SŁOWIANIN STANISŁAW:
Wiele się mówi o brytyjskim kolonializmie, w znacznej mierze dlatego, że Zachód poddaje się samokrytyce. Rosyjski rozwój miał wiele cech kolonialnych z podbojem ziem nad Bałtykiem (ale Litwa, Łotwa, Estonia, czy Finlandia są dzisiaj niepodległe), z podbojem dzisiejszej Białorusi, Ukrainy i Polski (wiadomo); z podbojem Syberii, czy Kaukazu. Terytorialnie, czy ludnościowo to mniej niż Brytyjczycy, ale zjawisko to samo. Czy Rosjanie o tym dzisiaj dyskutują? Czy Wy (Ty, Orteq, Wiesiek, Kalvarya) potraficie podjąć temat?
@Orteq:
No cóż, dwie wojny czeczeńskie mieliśmy za żywej pamięci, proszę Szanownego, nie wiem jak to można wyprzeć ze świadomości. Sądzisz, że ci wszyscy Tatarzy, Baszkirzy, Czuwasze, Mordwini, Udmurci, Maryjczycy, Kabardyjczycy, Ingusze, Komiacy, Karelowie, Buriaci, Jakuci, Tuwińcy, Chakasi, Ałtajczycy, Nieńcy, Awarowie, Dargijczycy, Lezgini, Lakowie, Tabasarowie, Rutulowie, Agulowie, Cachurzy, Kumycy, Nogajowie, albo Tatowie przylecieli do Federacji Rosyjskiej z Księżyca? To były wojny imperialne (nie zawsze podbijani mieli stworzone państwa, ale jeśli zrobimy z tego warunek to usprawiedliwimy Indian w rezerwatach), których Rosja dokonywała od XVI-XVII wieku.
PS.
Oczywiście, wyliczając dla Słowianina podbite narody już wyzwolone, dojechałem tylko do Nas i Ukrainy. A należałoby wspomnieć, że wyzwolili się Rumuni z Besarabii, Gruzini, Azerowie, Ormianie, Kazachowie, Uzbecy…
Amerykanskie boots on the ground dzisiaj
https://en.wikipedia.org/wiki/United_States_military_deployments
Wojska USA stacjonują dzisiaj w przynajmniej 50 krajach i innych terytoriach. A w ilu rosyjskie?
https://en.wikipedia.org/wiki/List_of_Russian_military_bases_abroad
„In 2018, it was reported that Russia operates at least 21 significant military facilities overseas.”
Pozostała obecność wojsk rosyjskich w innych jurysdykcjach to byle republiki sowieckie
Przypominajmy zbrodnie hipokrytów rzucających obecnie kamieniami w kierunku Rosji … Tak sobie myślę prywatnie … zrzucają kamienie z sumienia swojej formacji narodowej … a mordowali tubylców z bogiem na ustach …
Tzw. zbrodnie ZSRR są dziełem np. Ukraińców, Gruzinów, Azerów, Ormian, Kazachów, Uzbeków …. można mnożyć narodowości jak w tablicy Mendelejewa … Tak sobie myślę prywatnie … ZSRR nie jest liczbą rzeczywistą … przeciwnie …
Blog (szalonych)naukowców, miłosierne przytulisko dla obsesjonatów i nienawistników potłuczonych przez los?
Jagoda … bolszewicki Żyd … Tak sobie myślę prywatnie … tłukł niemiłosiernie … to nie był los … ale żywy człowiek …
Nic nie sadze PAKu (14:48).
Tam sa FAKTY geograficzno-historyczne. A te jakoś nie przypominają WIELKIEGO podbijania. W dawniejszych latach odbywało sie to bez ogromnych inwazji. Najczęściej zaś, były to decyzje gabinetowe.
Głównym faktem jest, iz Rosja carska, następnie ZSSR, a obecnie Rosja postsowiecka, w dalszym ciągu zajmują większość połaci globu. I jako takowa ‚jednostka’, ten najwiekszy terytorialnie kraj ma od wieków jakieś tam ‚zobowiązania’ wobec narodów czy jednostek administracyjnych, z którymi coś ja łączyło kiedyś.
A jak jest z twoim pupilkiem? No wiesz, z tym dzisiejszym jedynym imperium? Tam wciąż miłość bezdenna do Juesofej panuje no matter what?
PS. Jedno trzeba oddać ci bez bicia: sympatie w świecie plasują się po stronie bogatszej. A ta jest Ameryka. Wiec miałbyś i ty słusznego gdyby nie obecne pierepałki USA. No ale to osobny temat
@ Redes22
21 CZERWCA 2022 3:45
skrzywienie bardzie sugeruje cos nieliniowego
@PAK4 20 CZERWCA 2022 17:12
@markot 20 CZERWCA 2022 18:16
Mnie powiedziało „nachylenie i odchylenie”
Wartość rzeczywista = (nachylenie x liczba całkowita) + odchylenie
ja bym raczej skłaniał się zamiast odchylenia do definicji
(nachylenie x liczba całkowita) + stała
z tym ze i tu jest brak jasności, bo ta stała musi być liczba całkowitą.
Ale przyjmowanie na siłę polskich zamienników to tak jak nazywanie komputera licznicą albo mózgiem elektronowym
powracajac do pytania Markota
Arytmetykę stałoprzecinkową wciąż się stosuje tam, gdzie trzeba cos prostego policzyć i bardzo bardzo szybko.
Zamiast w domenie liczb rzeczywistych i zmienno przecinkowych, gdy na przykład trzeba wykryć drona, stosuje się dość zmyślne algorytmy. Na przykład CORDIC do obliczeń trygonometrycznych, fixed point fft.
Widmo częstotliwości rotujących wirników drona musi być wykryte w czasie rzeczywistym i monitorowane ciągle. Ponieważ wirnik moduluje światło odbite można go zidentyfikować po częstotliwości obrotów.
Ale, trwają prace, aby zmylić mozgi elektronowe dronami imitującymi owady albo ptaki.
Zabawa w kotka i myszkę trwa.
PAK4
21 CZERWCA 2022
14:48
Kolonizacja rosyjska, podboje, były DZIWNE….
Szlachta gruzińska, tatarska, polska, automatycznie stawały się szlachtą rosyjską.
Honorowane były nobilitacje nadawane przez poprzednich władców.
Takie kraje jak Gruzja, Armenia, same poprosiły o włączenie do imperium- zagrożenie tureckie.
Bułgaria, Rumunia, Finlandia, uzyskały niepodległość dzięki decyzjom carów.
Rosyjski najazd na Polskę, rozbiory, to fakt.
Taki sam jak amerykański najazd na Meksyk czy Kanadę, Hawaje, Filipiny.
Kiedy skończyla się dekolonizacja?
W latach 80′???
Ile jeszcze jest terytoriów zależnych od GB, USA, Francji?
Ile krajów jest zaleznych ekonomicznie?
Z kompradorami mianowanymi przez obce siły?
Za mało wiesz o historii świata, widzisz drzewo, nie las.
Trzymaj się tego na czym się znasz.
Albo, zmień źródła swej wiedzy, bo powtarzasz propagandowe bzdety
opryskiwanie czeresni nic mi nie dalo, deszcze zmyly olejek ochronny. Muszki zrobily swoje i czaresnie zgnily. Funt czeresni u nas kosztuje ok 6 dolarow.
Wisni nigdy w sklepie nie widzialem. 🙁
@Orteq:
Kaukaz, czy Syberia były podbijane zbrojnie. Z naszej własnej historii wiemy, że o ziemie Białorusi, Ukrainy, krajów nadbałtyckich Rosja się biła. Podobnie jak wiemy, że zwalczała powstania — począwszy od konfederacji barskiej, na Praskiej Wiośnie skończywszy (OK, doliczam braci Czechów). Zwalczała je zbrojnie, a nie gabinetowo. To były podboje. To myśmy się o nich nie uczyli w szkole, a podbijani byli w roli tych „biednych” i „niekulturalnych”, którym trudniej się przebić i dostąpić łaski współczucia ze strony cywilizacji. OK, może z wyjątkiem Czechów i 1968.
PS.
Tak, czytałem „Hadżi Murata”. Tołstoj tworzy jakąś nadzieję dla Rosji. Ale czy to stworzyło jakąś większą świadomość?
@SŁOWIANIN STANISŁAW:
1) Zauważ, proszę, że pisałem o carskiej i putinowskiej Rosji, a nie ZSRR. ZSRR dodaje do tej listy całkiem sporo.
2) Nie uważam, by istniały narody czyste i skażone, jeśli chodzi o zbrodnie. Wszyscy jesteśmy do nich zdolni. Są jednak narody, które mówią o swoich zbrodniach otwarcie, jak bywało w przypadku Polaków, Anglików, czy Niemców, a są takie, które w samozadowoleniu wypierają swój udział. Tu, niestety, mamy oprócz wielu państw bałkańskich, świetny przykład w Rosji i oficjalnej wykładni historii — a mieliśmy na dniach 350-tą rocznicę urodzin Piotra Wielkiego z wykładem historii prezydenta Putina. I to w tym samozadowoleniu i oficjalnej wykładni historii jest żywy, aktualny problem.
Dlaczego Ślązacy nie mogą mieć swojego państwa … kraj nad Wisłą nie jest Rosją … hunwejbini odmawiają nawet uznania Ślązaków jako NARÓD … Tak sobie myślę prywatnie … jako urodzony w Opolu … to skutek przyłączenie Śląska do macierzy … Donbas idzie w tym kierunku …
@wiesiek59:
> Honorowane były nobilitacje nadawane przez poprzednich władców.
A jakiś kontrprzykład? Bo ja wiem? Że III Rzesza w GG nie uznawała polskich tytułów szlacheckich?
> Bułgaria, Rumunia, Finlandia, uzyskały niepodległość dzięki decyzjom carów.
W przypadku Bułgarii i Rumunii carowie mieli duży wpływ na niepodległość, ale Finlandia w tym gronie to nieporozumienie.
> Taki sam jak amerykański najazd na Meksyk czy Kanadę, Hawaje, Filipiny.
Meksyk, owszem, choć Meksyku USA nie wcieliły do siebie. Osobna historia. Kanada też utrzymała niezależność — to zresztą część Brytyjskiej Wspólnoty Narodów…
Filipiny USA niejako zdobyły na Hiszpanii. Długa i wstydliwa historia dla USA, ale znowu — USA ich nie wcieliły do siebie, zawsze oficjalnie uznając tymczasowość zarządzania tym krajem. To więc inny przypadek niż Polska pod berłem carów.
Zostają Hawaje, które mają wiele z inwazji rosyjskiej na Krym w 2014… Tylko jakim cudem porównujemy wydarzenia różne o ponad 100 lat, przy całym rozwoju prawa międzynarodowego w międzyczasie, powstania najpierw Ligi Narodów, potem ONZ?
> Ile jeszcze jest terytoriów zależnych od GB, USA, Francji?
Trochę się znajdzie, ale nie jest tak łatwo je znaleźć na mapie. W żadnym przypadku nie jest to większość terytorium, a tak można by określić przykład Rosji…
> Ile krajów jest zaleznych ekonomicznie?
Co przez to masz na myśli? Bo my generalnie wszyscy jesteśmy od siebie zależni ekonomicznie.
PS.
Jeszcze raz to napiszę, bo już chyba wyraz dawałem — nie twierdzę, że z Zachodem jest wszystko w porządku. Twierdzę, że wytykając grzechy Zachodowi zupełnie zamykacie oczy na grzechy „wschodu” — zwłaszcza Rosji i Chin, bo to je wyciągacie jako pozytywne przykłady do przeciwstawienia Zachodowi. Niestety, we wszystkich „grzechach Zachodu” te kraje też mają swój udział, a w przeciwieństwie do Zachodu nie potrafią się z tego rozliczać.
@15:19
A u Szanownej wciąż miłość nieprzebrana? Do wszystkich bez wyjątku?
https://www.youtube.com/watch?v=OYkFiUsEQ8U
@PAK4
Że III Rzesza w GG nie uznawała polskich tytułów szlacheckich?
Lokalsi ich (formalnie) nie uznawali od 20 lat.
PAK4 podaj rozliczenia Zachodu ze swoich zbrodni … np. ile terytoriów zwrócono rdzennej ludności bez imperialnego nadzoru … zacznij od Israela … Tak sobie myślę prywatnie … liczby rzeczywiste nawróconych nie kłamią … rozliczenie to zwrot wzbogacenia … a nie mea culpa …
PAK4
21 CZERWCA 2022
15:55
Naprawdę masz poważne luki w wiedzy…
Doczytaj o Wielkim Księstwie Finlandii- na przykład…..
Czartoryski czy Badeni, mogli być ministrami u zaborców.
Podaj przykład ministra podbitych na przykład Indii, w rzadzie brytyjskim tamtych czasów.
Albo Meksykanina na wysokim urzędzie w USA.
Rasizm był i jest nadal dominujący w kręgach Anglosasów.
Zmienia się to dopiero od 20 lat.
W Turcji czy Rosji nigdy tego nie było.
I to podstawowa różnica cywilizacyjna.
Mówiąc o prawie międzynarodowym kpisz?
Czy tak na poważnie?
Nieznajomość faktów?
O ile dobrze pamiętam, w II RP zniesiono tytuły szlacheckie jako dające jakies przywileje prawne, majątkowe.
Ale, zwyczaj i powiązania towarzyskie pozostały.
Łącznie ze stratyfikacją społeczną.
Jakie sa grzechy Chin?
Te REALNE?
Nie medialne?
Jka ma się to do realnych wyczynów zachodnich demokracji?
Dlaczego w mediach nad Wisłą raporty zachodnich wywiadów publikowane są jak nekrologi … bez dziennikarskiej weryfikacji … Tak sobie myślę prywatnie … Kaczyński ma rację … polskojęzyczne media tubą obcych interesów … a ciemny lud to kupuje … zapewne blog nie jest wyjątkiem …
Tym oto sposobem, złowrogi Putin przez lata drenował Zachód przyjmując należności za energetyki WYŁĄCZNIE w metalu, po sztucznie zaniżonej cenie, gdzie papierowa waluta służyła WYŁĄCZNIE jako pomoc rozliczeniowa przy przeprowadzaniu transakcji. Kiedy zaś chińskie dolarowe rezerwy walutowe od 2013 roku przestały przyrastać po raz pierwszy od 2001 roku, to Zachód nawet nie zorientował się co to rzeczywiście oznacza, że oto chiński reżim zaczyna rozliczać się za eksportowaną tzw. chińską tandetę na takich samych zasadach, jak złowrogi Putin za swoje energetyki, co w istocie było częścią szeroko zakrojonego planu na odciągnięcie Europy z dolarowej strefy wpływów, jak również stanowiło początek końca hegemonii petrodolara i jego zakapiorów. Próbując przeciwdziałać rozwojowi wypadków, Grupa Trzymająca Władzę z początkiem 2014 roku zdobyła się jedynie na rozkręcenie kolorowej rewolucji, czy jak tam kto woli, majdanu, obłożenie złowrogiego Putina sankcjami, mając przy tym nadzieje na uwikłanie Imperium Zła w bezsensowną wojnę, która dodatkowo zrujnuje mu gospodarkę. Nie trwało jednak długo, nim złowrogi Putin przypieczętował przyjaźń z chińskim cesarzem wieloletnim kontraktem na dostawę energetyków,
https://businessoutsiderpl.wordpress.com/2020/03/30/prognoza-pogody-na-dlugi-weekend-czesc-1-sloneczko/#more-1234
==========
Stary tekst, nic nie stracił na aktualności.
Musi, PROROK…..
W telewizji o przyszłości kryptowalut.
Jakieś zawirowania w świecie liczb nierzeczywistych. Wszystko jest dla ludzi. Jak jest popyt to zawsze ktoś postawi stragan. Byłem jednym z pierwszych pod pałacem prezydenckim na Krakowskim Przedmieściu w Warszawie po katastrofie w dniu 10.04.2010 r., a stragan ze zniczami już tam stał
@wiesiek59:
Wielkie Księstwo Finlandii — ba! Było Królestwo Polskie, co to dla króla Aleksandra (rozumiem tego, co mu Kaczyński równy) pisano „Boże, coś Polskę”. Tylko jakimś dziwnym trafem ci miejscowi chcieli się sami rządzić, urządzali konspiracje, powstania…
Rasizm w Rosji? No właśnie rasizm. Zauważ, że mówisz o Polaku na wysokim stanowisku. To się mogło zdarzyć. Polak był biały, był Europejczykiem. (Ba! Tam się prosiło o „awans na Niemca”.) To tak, jakby chwalić angielską tolerancję, bo premierem Zjednoczonego Królestwa mógł zostać Szkot. A znasz przykład premiera Rosji z Dagestanu? Albo Kałmuka? Od jakiego roku w tej roli można sobie wyobrazić Żyda? BTW. To Rosjanie wyprodukowali „Protokoły Mędrców Syjonu”.
To samo dotyczy tej szlachty, o której uznaniu piszesz. Co to za argument? Z radżami Brytyjczycy też nie mieli problemów. Generalnie hierarchię budują rasa i klasa — nie znam przypadku, by lokalna arystokracja nie była traktowana jakoś lepiej i nie zachowała przywilejów, może w dłuższej perspektywie kolonie hiszpańskie, gdzie kolor skóry bardzo szybko przełożył się na klasy społeczne. (Stąd to moje dowcipkowanie o GG, bo w stosunku Niemców do Polski i Polaków było to samo — wyższość okupanta, ale w jakimś rachunku z klasą społeczną, czy — oczywiście i zwłaszcza — rasą, tak jak ją pojmowali.) To co piszesz o Rosji, to nie jest „lepszość” względem Brytyjczyków — to jest norma tego myślenia. Może tylko ludność azjatycka mniej się rzuca w oczy, niż ludność afrykańska.
Rosja zachowywała się zgodnie z wszystkimi regułami imperiów i ich podejściem do kolonii. Zresztą to, że w armii rosyjskiej w wojnie ukraińskiej mają dominować nie-Rosjanie, sugeruje że ich pozycja w państwie wciąż jest — zgodnie z regułami kolonialnymi — niższa.
A Chiny? Cóż, w 1950 roku napadły na Tybet i nadal go okupują. Ba! Wymuszają na świecie uznanie jego aneksji. Masz więc świeży przykład brutalnego budowania imperium kolonialnego.
O prawie międzynarodowym mówię serio. Wydawałoby się, że ludzkość czegoś się uczyła z pierwszej, a potem drugiej wojny światowej. Że się starała. A potem, popierając Hitlera, czy Putina, wywala się cały ten dorobek na śmietnik. Wiem, że porównanie grube, ale wszyscy wiemy, że kiedyś tam, państwa napadały na sąsiadów, że zapewne Mieszko „zjednoczył” Polskę przemocą, że Kazimierza Odnowiciela przynieśli na swoich włóczniach niemieccy najemnicy, że podbijaliśmy wiele razy Pomorze. Wiemy, że było niewolnictwo i pańszczyzna; że Polacy źle sobie poczynali na Kremlu za wielkiej smuty, że Napoleon sobie wojną podporządkowywał Europę, ale to wszystko jest jakaś tam barbarzyńska przeszłość. To dobrze wiemy i nie postulujemy przywrócenia handlu niewolnikami dla odtworzenia piastowskiej wielkości Polski — to jest dla nas już absurd. Tymczasem trwająca okupacja, czy trwająca wojna to nie jest przeszłość — to jest teraźniejszość, która woła by stanąć po stronie napadniętego. A potem przychodzicie napakowani postmodernistyczną propagandą, że wszystko jedno, że wszyscy źli, najlepiej narzekać i zabraniać innym działać, albo wręcz popierać morderców, bo co nas w naszym nihilizmie obchodzi jakieś prawo, czy jakaś moralność?
wiesiek59 21 CZERWCA 2022 10:40
Otóż to. Ale czy PAK4 to zrozumie?
ls42 21 CZERWCA 2022 18:44
A co Cię tam poniosło? Ja wtedy pojechalem zaraz nastepnego dnia do Santiago do Compostella w celu zlożenia podziękowań Opatrzności Bozej.
DE Compostella, do Św. Jakuba.
SŁOWIANIN STANISŁAW 21 CZERWCA 2022 16:11
Zgoda!!!
kaesjot 21 CZERWCA 2022 11:35
Racja!
Jagoda 21 CZERWCA 2022 15:19
O sobie piszesz?
Santiago de Compostela
Santiago = św. Jakub
PAK4 21 CZERWCA 2022 16:01
Czy Anglicy Szkoci i Walijczycy oraz Irlandczycy oddali Aborygenom Australię i wskrzesili wybitych przez nich „do nogi” Tasmańczyków? Co z rozliczeniem się przez Belgów z okrutnych zbrodni, które owi Belgowie popełnili w Kongo? Wreszcie co ze zwrotem Indianom terenów zabranych im przemocą i oszustwem przez Jankesów? Co też z odszkodowaniami dla Murzynów z USA (tzw. Afroamerykanów) za niewolniczą pracę ich przodków i za ich dyskryminację po dziś dzień? Kiedy też Niemcy wypłacą wreszcie nam Polakom odszkodowania za samo choćby barbarzyńskie zniszczenie Warszawy? Kiedy Izrael zostanie zmuszony przez Zachód do opuszczenia terenów nielegalnie odebranych Palestyńczykom? Kiedy wreszcie Zachód zmusi przywódców jego sojusznika, czyli Arabii Saudyjskiej, do przestrzegania choćby tylko elementarnych praw człowieka? Możesz nam więc wyjaśnić, dlaczego Zachód wciąż nie rozliczył się z w/w zbrodni na Ludzkości i dlaczego popiera on wciąż zbrodnicze reżimy, np. w Izraelu i Arabii Saudyjskiej?
Patrz też: https://www.academia.edu/81742823/Holokaust_żydowski_w_kontekście_światowej_historii_Jewish_Holocaust_in_the_context_of_world_history_
Link: https://www.academia.edu/81742823/Holokaust_żydowski_w_kontekście_światowej_historii_Jewish_Holocaust_in_the_context_of_world_history_
PAK4 21 CZERWCA 2022 19:05
1. Bo po prostu oni głupi byli i nadal są.
2. „Protokoły Mędrców Syjonu” wyprodukowali sami Żydzi.
3. Anglicy zawsze gardzili i do dziś gardzą Hindusami, poza tymi z najwyższej kasty.
4. Tybet zawsze był częścią Chin, tak jak np. Pomorze częścią Polski.
5. Prawo międzynarodowe jest nie do wyegzekwowania, gdyż w realnej polityce liczy się tylko siła: ekonomiczna, wojskowa etc. Polska nie podbijała zaś Pomorza, gdyż tam od dawien dawna mieszkali tam Słowianie Zachodni a nie Germanie. A przez Napoleona I, to zostaliśmy skłóceni na dobre z Niemcami i Rosją. 🙁
PAK4 21 CZERWCA 2022 15:55
1. Uznawała, np. tytuły byłych właścicieli Łańcuta, którzy przy pomocy Wehrmachtu wywieźli pod koniec wojny swoje skarby z Polski do Niemiec.
2. A co z Kalifornią, Nowym Meksykiem czy wreszcie, last but not least, Texasem?
3. Jest ich całkiem sporo i są to na ogół raje podatkowe i pralnie brudnych pieniędzy. 🙁
I co np. z Cyprem, gdzie brytyjskie eksterytorialne bazy zajmują aż 98 mil kwadratowych czyli 254 kilometrów kwadratowych (ponad 4% obszaru części Cypru należącego do UE)?
4. Tak jak pan (master) zależy od sługi (servant)?
Tymczasem upadł kolejny nierząd w Izraelu:
Koalicja rządząca Izraelem zagłosuje za rozwiązaniem parlamentu przed końcem miesiąca, jak poinformowało biuro premiera, przez co kraj czekają piąte wybory (wł. głosowanie) w ciągu trzech lat.
Upadek koalicji nastąpił po tygodniach paraliżu spowodowanego odejściem dwóch prawicowych ustawodawców i częstymi buntami trzech innych, przez co koalicja premiera Naftalego Bennetta nie ma już większości w parlamencie. Wskutek tego koalicja premiera Naftalego Bennetta przestała być większościowa w parlamencie.
Wybory, które mają się odbyć jesienią, przypadają w napiętym okresie po wzroście liczby palestyńskich ataków na Izraelczyków i eskalacji wojny w cieniu między Izraelem a Iranem.
Obecna umowa koalicyjna przewiduje, że Yair Lapid, minister spraw zagranicznych i centrysta, były dziennikarz radiowy, obejmie stanowisko tymczasowego premiera w przypadku, gdyby prawicowe ugrupowania zrezygnowały z udziału w przedterminowych wyborach. Jeśli porozumienie zostanie dotrzymane, Lapid będzie kierował rządem przez co najmniej kilka miesięcy.
NYT
Rubel wystrzelił. Rosyjska waluta najmocniejsza od siedmiu lat. W tym roku wartość rubla rosyjskiego na rynku wzrosła o 35%, co jest rekordem na skalę światową. Rubel wzrósł tym samym do swojego maksimum.
https://next.gazeta.pl/next/7,151003,28606196,rubel-wystrzelil-rosyjska-waluta-najmocniejsza-od-siedmiu-lat.html#do_w=52&do_v=303&do_st=RS&do_sid=602&do_a=602&s=BoxBizImg8
PAK4 – 15:46
„Kaukaz, czy Syberia były podbijane zbrojnie. Z naszej własnej historii wiemy, że o ziemie Białorusi, Ukrainy, krajów nadbałtyckich Rosja się biła…”
A z kim biła?
Trzy rozbiory Polski, wszystkie dokonane przez TRZECH rozbiorców, odbyły się nie-zbrojnie. Późniejsze pierepałki tez nie figurują w historii jako jakieś zaborcze napaści zbrojne. Najgorsza z tych napaści, dokonana 17 września 39 roku, nie słynie z rozlewu krwi polskiej na wschodzie kraju. Ona była rezultatem ugody dwóch ówczesnych najwyższych czynowników mocarstwowych, Ribbentropa i Mołotowa. Zmobilizowana świeżo armia II RP dostała prikaz stania z bronią u nogi i niedlugo potem rekruci zostali rozpuszczeni do domów. Mojemu ojcu zajęło dwa tygodnie by na piechotę doturlać się do domu, po 7-tygodniowej „kampanii wrześniowej”.
Tylko kadra oficerska była internowana i nieszczęśliwcy, którzy zostali negatywnie przenicowani przez sito NKWD, trafili do Katynia i kilku innych miejsc stalinowskiej kaźni.
Takie przypomnienie paskudnego etapu naszej historii. Do dziś przypominającego nam powody do nieprzemijającej nienawiści do Rosji. O wiele większej niż do Niemiec. Nawet tych straszną III Rzeszą skażonych.
Tak już mamy i nikt nam tego nie odbierze.
21 czerwca 2022 roku godzina 6.29
Ta data, a szczególnie ta godzina co do minuty, pozostaną na zawsze w historii Polski.
Wicepremier Jarosław Kaczyński oznajmił, że rezygnuje z zajmowanego stanowiska w rządzie i wyznaczył następcę w osobie Mariusza Błaszczaka.
Dopiero o godzinie dziewiątej rozpoczęła się popularna od 51 lat audycja „Lato z radiem” melodią „Polka Dziadek”
calvarya01
20/6/22
Dobranoc!
Jeden z Twoich najlepszych i najbardziej wnikliwych wpisow. Tak trzymac. Wiem, wiem mialo mnie juz tu nie byc. No coz. Mysle, wiec znowu jezdem.
Tak mi wpadło w oko — ku uciesze kalvaryi:
https://1.bp.blogspot.com/-w2mB0jghHW0/YUxXfIBBQXI/AAAAAAABbT4/zVIkyBN176wgDgdJACWZ-XJndfa2X-xMQCLcBGAsYHQ/s540/242086861_10159988982276518_6443244909247195232_n.jpeg
@Orteq:
Było trochę wojen w XVII wieku, zresztą i wcześniej, przy okazji zbierania „ruskich ziem”, bo skąd była odwoływana polska armia do obrony przed Szwedami w czasie Potopu? Nie tylko z Ukrainy.
Były powstania. A też przypomnę, że zarówno konfederacja barska, jak i powstanie kościuszkowskie miało miejsce w Polsce, ale w obu przypadkach tłumiła je armia rosyjska, jako pokaz zbytniej niezależności. (BTW. Kto stłumił powstanie węgierskie, to z armią siedmiorodzką Bema?) Mamy też kampanie wojenną w 1792, że tak nieśmiało przypomnę — II rozbiór wynikał z podboju rosyjskiego. BTW. Ja raczej unikam tu napaści z okresu ZSRR, choć wymieniłem stłumienie praskiej wiosny, jako ostatni przykład. Choć mogłem dać Kabul i 1979. W każdym razie, ten najgorszy 17 września, wcale nie jest najgorszy w rzeczywistości.
@kalvarya01:
> Czy Anglicy Szkoci i Walijczycy oraz Irlandczycy oddali Aborygenom Australię i wskrzesili wybitych przez nich „do nogi” Tasmańczyków?
Oddali miejscowej ludności. Że stała się ona anglosaska… Cóż, to co Pane chcesz zrobić? To jak z pytaniami o Izrael — oddać Palestyńczykom, OK, ale co zrobić z Żydami? Takie oddawanie, jak postulujesz, wymagałoby wymordowania, albo wypędzenia milionów ludzi — Anglosasów (i innych „białych”) z Australii, Rosjan z państw bałtyckich, Krymu, czy Kaukazu, Żydów z Izraela.
Ja tylko oczekuję, że jeśli ludzie na miejscu powiedzą, że chcą być niepodlegli, to nie będzie się zrzucać na nich bomb, jak to robiła Rosja w Czeczenii i jak to robi w Ukrainie. Albo, jeśli chcesz innych przykładów, jak to robił Irak, czy Turcja z Kurdami.
> „Protokoły Mędrców Syjonu” wyprodukowali sami Żydzi.
A Pan sobie sam wystawiłeś świadectwo.
> Anglicy zawsze gardzili i do dziś gardzą Hindusami, poza tymi z najwyższej kasty.
A Pakistańczyka wybrali burmistrzem Londynu?
> Tybet zawsze był częścią Chin, tak jak np. Pomorze częścią Polski.
Teraz wszystko jasne — Katarzyna Wielka prowadziła do rozbiorów Polski, bo jako szczecinianka z urodzenia, chciała przyłączenia Rosji do polskiej macierzy :LOL:
> Prawo międzynarodowe jest nie do wyegzekwowania
Interwencja w Korei miała „papiery z ONZ”. Interwencja wyzwoleńcza dla Kuwejtu, miała szerokie poparcie międzynarodowe. W przypadku wojen w byłej Jugosławii, osądza się zbrodniarzy ze wszystkich stron. To nie jest, że się nie da tak w ogóle. To jest tak, że różni paleo-konserwatyści wciąż lansują ideę międzynarodowego prawa dżungli i często (choć nie zawsze), udaje im się egzekucję torpedować. Tak jak storpedowali postępowanie ONZ przeciwko Rosji w sprawie Ukrainy, choć mieli mniejszość.
> A co z Kalifornią, Nowym Meksykiem czy wreszcie, last but not least, Texasem?
USA miały Meksyk „na dłoni”. Mogły anektować cały. Fakt, przestraszyły się odsetka „niebiałej ludności” i niepodległość Meksyku uratował wtedy amerykański rasizm. Ale Wy nie mówicie o tym, co dało Meksykowi niepodległość, tylko sugerujecie, że USA tam rządzi. No to nie rządzi i nawet tego nie chce 😛
> Jest ich całkiem sporo i są to na ogół raje podatkowe i pralnie brudnych pieniędzy.
Coś jak Osetia Południowa?
> Tak jak pan (master) zależy od sługi (servant)?
Przez Wieśka bodaj lubiany Jordan Petersen tłumaczy, że jak hierarchia społeczna istnieje wśród homarów, to nie ma co jej unikać u ludzi. Ja się z tego śmieję, ale gdy mowa o istnieniu jakiejkolwiek hierarchii, wyższości i niższości, to się wydaje ona jakoś rzeczywiście uniwersalnym prawem. Czy Polska miała w Układzie Warszawskim, czy RWPG prawa równe ZSRR?
Pytanie raczej o granice hierarchii i poziom równości. O prawa człowieka, prawa obywatelskie, czy choćby minimalne prawa międzynarodowe. Ja się o to dobijam, a Ty mówisz, że albo wszystko — rewolucja, absolutna równość, komunizm — albo nic: zamordyzm, zamordyzm, zamordyzm.
PAK4
21 CZERWCA 2022
19:05
Nie przyswajasz argumentów…..
Prawa Człowieka to jedynie ozdobnik retoryczny, dobrze brzmiacy w publikacjach.
Stosowane są WEWNĄTRZ krajów zwących się demokratycznymi i to od niedawna.
Ot, wymysł propagandowy BIAŁYCH mający obowiązywać w krajach przeciwników….
Tybet był podbity przez Mongołów, potem, wpadł w zależność od Chin.
Podbój przez armię Mao przyniósł zmianę stosunków z feudalnych na bardziej cywilizowane.
Nie podoba ci się uprzemysłowienie, parcelacja ziemi, powszechne nauczanie?
Trudno….
Sprawa Kuwejtu….
Amerykańska ambasador wyraziła się jasno.
USA nie będzie miało nic przeciwko aneksji przez Irak.
To miała być rekompensata kosztów wojny z Iranem.
Ale, odwidziało się Bushowi….
Mieliśmy szansę podporządkować sobie Moskwę, niestety Władysław III widział siebie w roli cara, nie swego syna.
I dziejowa okazja przepadła…
Dziejów historii najnowszej nie znasz kompletnie.
Nie ma nawet sensu linkować, bo i tak nie czytasz.
Zamknięty umysł wypełniony propagandową papką.
Czy Stany Zjednoczone nadal korzystają z pracy przymusowej w swoim systemie więziennictwa?
Główne korporacje czerpiące zyski z niewolniczej pracy więźniów to Motorola, Compaq, Honeywell, Microsoft, Boeing, Revlon, Chevron, TWA, Victoria’s Secret i Eddie Bauer.
IBM, Texas Instruments i Dell otrzymują płytki drukowane wykonane przez więźniów z Teksasu. Więźniowie z Tennessee szyją dżinsy dla Kmart i JCPenney. Dziesiątki tysięcy młodzieży przerzucającej hamburgery za minimalną płacę w McDonald’s noszą mundury szyte przez pracowników więziennych, którzy są zmuszani do pracy za znacznie mniej.
W Kalifornii, podobnie jak w wielu stanach, więźniowie, którzy odmawiają pracy, są przenoszeni do mieszkań dyscyplinarnych i tracą przywileje w stołówce, a także kredyt na „dobry czas”, co odcina im karę.
Systematyczne maltretowanie, bicie, przedłużająca się izolacja, deprywacja sensoryczna i brak opieki medycznej sprawiają, że warunki więzienne w USA należą do najgorszych na świecie. Jak na ironię, praca w wyczerpujących warunkach za grosze na godzinę jest traktowana jako „dodatek” za dobre zachowanie.
W grudniu [2010] gruzińscy więźniowie rozpoczęli strajk i odmówili opuszczenia swoich cel w sześciu więzieniach przez ponad tydzień. W jednym z największych protestów więziennych w historii USA więźniowie mówili o zmuszaniu do pracy siedem dni w tygodniu bez wynagrodzenia. Więźniowie byli bici, jeśli odmawiali pracy.
Wysłane przez: Paul Greenwood | 21 czerwca 2022 18:25 utc | 14
==========
Prawa Człowieka…..
Trochę o Ujgurach- z drugiej strony medialnego frontu.
Zachodnie media są w stanie wypaczyć wszystko.
A Guantanamo … Tak sobie myślę prywatnie … a czepiają się majtek Nawalnego … za ciasna gumka …
gruzińscy więźniowie rozpoczęli strajk (…)W jednym z największych protestów więziennych w historii USA
To ta Gruzja, gdzie jeździ się samochodami marki Bród, Unik i Rtęć?
Z Wybiórczej o szkole:
Mówi się, że piątkowi uczniowie w przyszłości będą pracować u tych trójkowych. Prymusi często uczą się dla ocen, nie dla wiedzy. Dla rodziców, nie dla siebie. Skupieni wyłącznie na stopniach, nie mają czasu nauczyć się życiowej zaradności, bo wszystko inne robią za nich rodzice. A kiedy skończą studia i przychodzi im się zmierzyć z prawdziwym życiem, pojawia się kryzys. Nie mają pojęcia, co chcą robić, bo nic o sobie nie wiedzą. Przez ponad 20 lat spełniali cudze oczekiwania i dziś są dobrze wykształconymi analfabetami życiowymi.
https://weekend.gazeta.pl/weekend/7,177333,28604716,nie-da-sie-budowac-relacji-z-dzieckiem-slowami-jestes-glabem.html
markot 22 CZERWCA 2022 7:46
Tak, ci od Stalina, tyle że wdług PAK4, to Rosją zawsze Rosjanie rządzili, a wiec chyba jednak ci z Hameryki czyli inaczej Indinie, albo, jak kto woli, Hindusi.
I said Gruzja
Oh Gruzja… on my miiiind,
PAK4 22 CZERWCA 2022 5:34
Masz wyraźnie głęboko uwarunkowane integralne kompleksy swego superego na tle swojej społecznej samoidentyfikacji genderowej w kontekście sztuk wizualnych stylu socrealistycznego spowodowane załamaniem się u ciebie, na skutek przeżyć we wczesnym dzieciństwie (kompleks Edypa etc.), fali prawdopodobieństwa w kontekście niekopenhaskiej interpretacji zjawiska tunelowania na poziomie makro, zgodnie z teorią fali fazy (l’onde de phase) Xięcia Louisa Victora Pierra Raymonda de Broglie (z TYCH de Brogliów).
Ukłony,
Twój Analityk
O, my Suliko from Atlanta, Georgia…
Gdzie rozkwita kwiat róży kwiat
Na gałązce siadł lotny ptak
Zadrżał wśród listowia purpurowy pąk
Czemu serce drży Suliko
Zadrżał wśród listowia purpurowy pąk
Czemu serce drży Suliko
Jedzie wrony koń zpoza wzgórz
Jeździec zbliża sie wchodzi w próg
Spragnionemu dajże wody wyjdź przed dom
Czemu kryjesz się Suliko
Spragnionemu dajże wody wyjdź przed dom
Czemu kryjesz się Suliko
Pięknie pachnie chleb pachnie miód
Prosze napij sie ucisz głód
Ale nadaremnie ściga mnie twój wzrok
Inna jestes już Suliko
Ale nadaremnie ściga mnie twój wzrok
Inna jestes już Suliko
Wiłam z przędzy nic długą nic
Z nici powstał szal zwiewny szal
Szal do przędzy niepodobny nic a nic
I ty jestes juz nie ten sam
Szal do przędzy niepodobny nic a nic
I ty jestes juz nie ten sam
Pobladł jeździec i ruszył w cwał
W locie zerwał kwiat róży kwiat
Zdrada rani serce kolec rani dłoń
Zapłakała w głos Suliko
Bo umiera miłośc kiedy stargasz ją
Mówi stara pieśń Suliko…
Я могилу милой искал, Сердце мне томила тоска. Сердцу без любви нелегко. Где ты? Отзовись, Сулико. Увидал я розу в лесу, Что лила, как слезы, росу, Ты ль так расцвела далеко, Милая моя Сулико? Над любимой розой своей Прятался в ветвях соловей. Я спросил, вздохнув глубоко, Ты ли здесь, моя Сулико? Клювом к лепесткам он прильнул, И, лесов будя тишину, Зазвенела трель соловья, Будто он сказал: «Это я!»
https://www.shazam.com/pl/track/6048446/suliko
@wiesiek59 22 czerwca 2022 6:32
Mieliśmy szansę podporządkować sobie Moskwę, niestety Władysław III widział siebie w roli cara, nie swego syna.
Zygmunt III i rozchodziło się bardziej o nie podlegające negocjacjom żądanie Rosjan by ów syn – późniejszy Władysław IV, przeszedł z katolicyzmu na prawosławie. Cóż za różnica ze współczenym Zygmusiowi Henrykiem de Bourbon, dla którego Paryż wart był mszy.
Na podporządkowanie też nie było szans, to był zbyt duży kąsek do połknięcia dla ówczesnej Rzp-litej.
markot
22 CZERWCA 2022
7:46
Z uporem maniaka, tłumacz S-3 wpisuje zamiast Georgia, Gruzja.
I tyle….
Dyskusje o literówkach, niewłaściwości portali, niewłaściwych autorach, zastępują dyskusje o treści artykułów.
Świadczy to o poziomie czytających.
Herstoryk
22 CZERWCA 2022
8:33
Fakt, mój błąd….
Ale wniosek prawidłowy.
To samo zresztą można odnieść do Henryka VIII,
Głupota papieża spowodowała schizmę.
Stracił dochody i angielskich wiernych.
Władcy to tylko ludzie popełniający błędy.
Nie inaczej jest i obecnie- durnota unijnych komisarzy poraża.
wiesiek59,
no OK, nie czytasz sam tego, co rzucasz nam, tym ponizej Twojego poziomu.
Kiedys pisales o Etiopii i Abisynii, jak o dwoch roznych krajach. Tez wina translatora?
Miej troche dystansu do siebie i smiej sie razem z nami. To naprawde zdrowe.
PAK4 22 CZERWCA 2022 6:01
1. Chcę zwrócić Australię, Amerykę i Palestynę ich prawowitym właścicielom. Wedlug prawa tylko tereny czy budynki zajęte w dobrej wierze można uzyskać na własność poprzez tzw. zasiedzenie, ale nie takie zdobyte siłą czy podstępem. Żydzi mogą zaś wrócić do siebie, czyli do Chazarii. Putin chyba nie będzie mieć nic przeciwko temu. A ktoś, kto zamieszkuje na cudzym terenie prawem kaduka, zasługuje tylko na wypędzenie.
2. To dlaczego uważa się np. bojowników o wolność i jedność Irlandii, Baskonii czy Katalonii za terrorystów, więzi ich, prześladuje etc.? Dlaczego Turcja może okupywać Kurdystan? Bo jest w NATO i jest, tak jak Ukraina, kandydatem do UE?
3, Jaki jest naukowy, czyli empiryczny dowód na to, że to nie Żydzi z carskiej Ochrany wyprodukowali te protokoły? Przecież tego na 100% nie mogli zrobić goje (goim), a piszę to jako stary żyd: „Nazywam się Lech Keller czasami używam Krawczyk (spolszczone żydowskie -Sznajder) mam lat 70 plus jestem Żydem i homoseksualistą” (Fronda).
4. Nie Anglicy, a „Ciapaci”, „żółci” i „czarni”, którzy dziś stanowią większość mieszkańców Wielkiego Londynu.
5. Tybet zawsze był częścią Chin, tak jak Mazowsze, formalnie długo bedące niepodległym xięstwem, było i jest częścią Polski – masz dowód na to, że było inaczej?
6. Te „papiery z ONZ” były uzyskane drogą oszustwa, Kuwejt to sztuczny twór brytyjskiego kolonializmu, rozpad Jugosławii spowodowany był przez poparcie Zachodu dla Ustaszy i innych skrajnie nacjonalistycznych elementów np. w Kosowie. Globalnie na świecie panuje przecież prawo dżungli – inaczej to nikt by nie wyrzucał pieniędzy na wojsko.
7. Co to znaczy, że USA miały Meksyk „na dłoni”? To tak samo, jakby powiedzieć, że Niemcy miały w roku 1939 Polskę „na dłoni”, ale nie dołączyli jej od razu w całości do Niemiec, poza Pomorzem, Śląskiem, Wielkopolską i częścią Mazowsza, bo przestraszyli się odsetka „niegermańskiej ludności” i utworzyli tzw. GG. Ale tak jak Niemcy po roku 1990 skolonizowały gospodarczo Polskę, tak samo USA zrobiły, i to znacznie wcześniej, z Meksykiem, obecnie będącym razem z Kanadą protektoratem USA w ramach tzw. Nafty.
8. Śmieszny jesteś wstawiając Osetię Południową do tej samej przegródki co np. Monako, Bahamy albo Liechtenstein czy nawet Cypr Południowy („grecki”).
9. W każdym stroju klasowym istnieje hierarchia społeczna. W Układzie Warszawskim i w RWPG, to Polska była numerem dwa, zaraz po ZSRR. W NATO i UE jesteśmy zaś, w najlepszym wypadku, dopiero gdzieś pod koniec pierwszej dziesiątki.
10. No więc jak to jest z tymi prawami człowieka w Palestynie – nielegalnie okupowanej przez Izrael, jak jest z nimi w Arabii Saudyjskiej – arabskim sojuszniku numer 1 USA na Bliskim Wschodzie? Poza tym, to komunizm oznacza równość szans, a nie absolutną równość. Natomiast w realnym kapitalizmie musi panować zamordyzm, aby utrzymać klasy niższe w podległości do klas wyższych.
Szalom z okolic Ger!
markot 22 CZERWCA 2022 7:46
To jest ta sama Gruzja, gdzie jeździ się też osobówkami marki Zomosuki i furgonetkami marki Ochida.
@PAK4 – Kolejny dowód na upadek, tym razem „prawno-socjalny” tzw. Zachodu:
W USA i wielu państwach europejskich, chcąc ograniczyć przestępczość i pokazać obecność policji na ulicach, polecono funkcjonariuszom legitymowanie i nękanie podejrzanych i tych których znają z różnych wyskoków. Długo to nie trwało, bo zaraz zaczęły się wpierw jęki a potem mocne działania tzw. obrońców praw człowieka, w rezultacie czego akcja spaliła na panewce. Dlaczego?
Nie chcę tu dokładnie tłumaczyć, bo albo dostanę bana albo/i zostanę posądzony o …………. (piłkarze mają to na rękawkach).
Po prostu padły pytania, dlaczego legitymuje się takich ludzi a nie innych. Policja coś tam tłumaczyła się, że właśnie takich mają na widelcu, itp. itd. Karykaturą stały się więc sprawdzania kobiet w wieku emerytalnym, czy też statecznych panów i akcja została wygaszona.
W Chicago uważają zaś widocznie, że jak ktoś ucieka, to po prostu lubi sobie pobiegać i co komu do tego.
https://wiadomosci.gazeta.pl/wiadomosci/7,114881,28608121,chicago-policja-wprowadza-nowy-regulamin-sledczy-nie-moga.html#do_w=57&do_v=428&do_st=RS&do_sid=750&do_a=750&s=BoxOpLink
Strajk kolejarzy w Wielkiej Brytanii
Wielka Brytania została we wtorek dotknięta największym od trzech dekad strajkiem kolejarz, który zapoczątkował to, co liderzy związkowi i rządowi ostrzegli, że może to być lato niepokojów pracowniczych.
NYT
KolejarzY. Co nagle, to po Diable…
act
22 CZERWCA 2022
9:21
Do niedawna były to nazwy wymienne.
Coś na ten temat pisałem?
wiesiek59,
w Twoim wpisie to byly dwa rozne panstwa istniejace wspolczesnie. Nie kaz mi cytowac siebie i mojej nan reakcji. To naprawde nieistotne.
Niech ten rzuci pierwszy kamieniem etc.
BTW. sporo korzystam na Twoich wpisach.. jesli, czyli prawie nigdy, potrafisz je dozowac.
act
22 CZERWCA 2022
10:20
Od 6 roku życia wpadłem w nałóg.
POŻERANIA słowa pisanego..
Więc wybacz.
Zmieniając jedno słowo w tytule- Przeciwko FAKTOM rzeczywistym, zdecydowanie pisałbym na temat.
Stopień manipulacji jest niesamowity.
Trzeba sięgnąć po 1984 dla odświeżenia pamięci.
Orwell świetnie opisywał mechanizm.
A nasze owce?
Nikt im nie udowodni że czarne jest czarne…..
Skoro MENDIA twierdzą coś przeciwnego.
Czy język angielski, hiszpański, portugalski, francuski można mnożyć poza Europą … są językami tubylców czy językami kolonizatorów … o symbolu Jezusa na krzyżu nie wspomnę … Tak sobie myślę prywatnie … a czepiają się litery Z … jak Zorro … i języka rosyjskiego w Donbasie …
Wracając do statystyki – „biased” to znaczy „obciążony” (w domysle błędem):
Po angielsku:
The bias of Theta„^” is defined as B(Theta„^”) = E(Theta„^”) – where (Theta„^”) is an estimator. It is the distance between the average of the collection of estimates, and the single parameter being estimated. The bias of Theta„^” is a function of the true value of Theta so saying that the bias of Theta„^” is “b” means that for every Theta the bias of Theta„^” is “b”.
There are two kinds of estimators: biased estimators and unbiased estimators. Whether an estimator is biased or not can be identified by the relationship between E(Theta„^”) – Theta and zero.
If E (Theta„^”) – Theta NOT = 0, Theta„^” is biased.
If E (Theta„^”) – Theta = 0, Theta„^” is UNbiased.
Po polsku:
Definicja estymatora pozostawia dużą dowolność w wybraniu danej statystyki do szacowania parametru, nie pozwalając jednocześnie na ocenę, która ze statystyk jest „dobrym” estymatorem. Aby sprawdzić, czy dana statystyka jest dobrym kandydatem na estymator parametru, sprawdza się czy spełnia ona zestaw własności charakteryzujących estymator.
Nieobciążoność : estymator jest nieobciążony gdy wartość oczekiwana rozkładu estymatora jest równa wartości szacowanego parametru, ale jeśli różnica pomiędzy wartością oczekiwaną rozkładu estymatora a wartością szacowanego parametru jest zależna funkcyjnie od estymatora, to estymator nazywany jest obciążonym, zaś sama różnica nazywana jest obciążeniem estymatora.
(Wikipedia)
wiesiek59,
mysle, ze rozumiem dobrze Twoja pasje.
Gruzja w moich myślach – ulubiona piosenka tow. Generalissimusa Stalina i tow. tow. Kaczyńskich:
Gruzja, Gruzja
Przez cały dzień (przez cały dzień)
Tylko stara, słodka piosenka
Gruzja ciągle w głowie (Gruzja ciągle w głowie)
Powiedziałem Gruzja
Gruzja
Twoja piosenka (twoja piosenka)
Przychodzi tak słodka i czysta
Jak światło księżyca przez sosny
Inne ramiona wyciągają się do mnie
Inne oczy uśmiechają się czule
Wciąż w spokojnych snach widzę
Droga prowadzi z powrotem do ciebie
Powiedziałem Gruzja
Oh Gruzja, nie znajdę spokoju (nie znajdę spokoju)
Tylko stara, słodka piosenka
Gruzja wciąż w mej głowie (Gruzja w mej głowie)
Inne ramiona wyciągają się do mnie
Inne oczy uśmiechają się czule
Wciąż w spokojnych snach widzę
Droga prowadzi z powrotem do ciebie
Łuha-łuha, Gruzja
Gruzja
Żadnego spokoju, żadnego spokoju nie znajdę
Tylko stara, słodka piosenka
Ciągle w głowie Gruzja (Gruzja w głowie)
Powiedziałem, że tylko stara, słodka piosenka
Gruzja w moim umyśle.
https://www.youtube.com/watch?v=fRgWBN8yt_E
1400 kilometrów na hulajnodze z Bieszczad nad Bałtyk w celu charytatywnym, a w planie 2500 kilometrów po 200 górskich szczytach to zamierzenie młodego sportowca.
Staram się trzymać tylko liczb rzeczywistych.
Tymczasem zza granicy napływają codziennie dane o zabitych. Jak na taką skalę wojennych działań te liczby wydają się zaniżone. Rosja nie podaje danych o stratach od trzech miesięcy.
Nagi mężczyzna szalał po Rynku w Krakowie. Najpierw prowadził samochód, a potem uciekał pieszo przed goniącymi go strażnikami
Za zjednoczenie Niemcy są wdzięczni Rosjanom … Tak sobie myślę prywatnie … to dowód na zwrot zajętego terytorium NRD do macierzy … o Austrii nie wspomnę … a przymusu nie było … podobnie z z republikami po rozwiązaniu ZSRR … czy na taki gest stać potomków kolonizatorów … Aborygenia zamiast Australia … Kri i inne zamiast Kanada …
SŁOWIANIN STANISŁAW 22 CZERWCA 2022 10:48
Otóż to!
Od 6 roku życia wpadłem w nałóg.
POŻERANIA słowa pisanego..
Nie tylko ty.
Ale po co to pożarte natachmiast wyrzygiwać w takich ilościach?
To zakrawa na bulimię.
Może najpierw przeżuć, przetrawić i wyekstrahować dla organizmu przydatne, a resztę wydalić w ustronnym miejscu?
Stalin, to byl czutnyj czielawiek, podobno i lze uronil przy Suliko… potem dla rownowagi, kazal rastrieliac kilku, co nie rozumieli… muzyki.
czutkij?
@kalvarya
Widzę, że się zreflektowałeś po czasie i nadrabiasz ciężkawo, a @act załapał od razu 😎
… Może nie zawłaszczyłeś jeszcze tego bloga, kiedy rozmawialiśmy o markach samochodów amerykańskich?
Bez ZSRR katolicka III Rzesza mogła sięgać od Atlantyku do Pacyfiku z pomocą kolaborantów przodków dzisiejszych członków NATO … wykaz pod Stalingradem … Tak sobie myślę prywatnie … rzucając kamień w kierunku Rosji … warto myśleć historycznie … i zacząć porządkowanie świata od siebie … zamiast uber alles …!
Mercury, byl taki samochod?. Bo Ford i Dodge to jasne.
markot 22 CZERWCA 2022 10:56
Czerwony Szewrolet, Szewrolet Antylopa, Szewrolet Przesunięcie,
Generał Silnik Kanion,
Unik Durango,
Dżip Pastuch, Dżip Szeroki,
Bród Dziki Koń, Bród Ucieczka, Bród Ekspedycja, Bród Wybuchający,
Linkoln Nawigator, Linkoln Kontynetalny etc. etc.
Oto bowiem minęło 145 lat i znowu po Polsce i Europie Środkowo-Wschodniej hulają brytyjscy agenci i politycy, chcący miejscowych Słowian rzucać przeciw Rosji po to tylko, by Brytania odzyskała dominującą pozycję na początek europejską, a docelowo także na obszarach Bliskiego i Środkowego Wschodu.
Różnica polega głównie na tym, że w 1877 r. książę Sapieha nie był bynajmniej obcym agentem, zapytał o konkrety obiecywanej Polakom brytyjskiej pomocy, a gdy zamiast nich usłyszał tylko ponowne zachęty i ogólniki – rozwiązał swój nieszczęsny „Rząd” i odwołał wszelką akcję powstańczą, jako z góry skazaną na klęskę prowokację. Niestety, dziś na taki przykład odpowiedzialnego patriotyzmu wśród polskich liderów politycznych liczyć już nie możemy.
https://marucha.wordpress.com/2022/06/20/wielka-gra-bis-co-anglicy-robia-na-ukrainie/
@act – Mercury to nieistniejący już oddział amerykańskiego producenta samochodów Ford Motor Company (Fabryka Silników Pana Broda). Stworzony w 1938 roku przez Edsela Forda, Mercury był sprzedawany jako marka o średniej cenie przez prawie cały okres istnienia, wypełniając lukę cenową pomiędzy liniami modeli Ford i Lincoln.
@act:
Linkowałem i potem mi się bardzo spodobało. Cały czas nuciłem: Glinka-Czajkowski-Rimski-Korsakow. No to wrzucam jeszcze raz, choć w sumie niektórzy tu są świadomymi stalinistami:
https://www.youtube.com/watch?v=4MPyYYrAWb8
markot
22 CZERWCA 2022
10:51
Wyrażam się raczej kulturalnie.
I nie RZYGAM….
Pewnych słów w towarzystwie się nie używa.
Kup sobie Kamyczka, albo przypomnij zasady zachowania się.
wiesiek59 22 CZERWCA 2022 11:25
Przypominam nie tak znów dawną wyprawę na Kijów pewnego samozwańczego marszałka Juozasa Pilsudskisa – pochodzącego z Liwy polskojęzycznego agenta austriackiego wywiadu.
PAK4 22 CZERWCA 2022 11:26
Kto tu jest Stalinistą oprócz Ciebie?
Z partyjnym pozdrowieniem.
Tow. Sznajder
@kalvarya01 22 CZERWCA 2022 10:38
Widzę, że na tym blogu o nauce, to nikt oprócz Mnie (I) nie pojmuje nawet elementarnej statystyki matematycznej. 😉
@act
Jak widzisz, napalony prymus już zanurkował w Wiki, więc tylko dodam, że od 11 lat Mercury już nie jest produkowany. A próbowali nawet robić hybrydy, bez większego powodzenia.
markot 22 CZERWCA 2022 11:38
Turystyczna kuchenka benzynowa, ale czy też made in China?
act 22 CZERWCA 2022 10:53
Чуткий to po polsku wrażliwy. Od razu widać u ciebie braki w edukacji… 🙁
„Od 6 roku życia wpadłem w nałóg.
POŻERANIA słowa pisanego.. ”
„Ale po co to pożarte natachmiast wyrzygiwać w takich ilościach? ”
……………..
to się trzyma kupy bo pożerane wymaga ew. łykania aby potem nie pisać ” ja tego nie łykam ” .
Nikt nie wymaga przecież od nikogo ani od siebie aby łykał wyrzygane .
Wyrzygiwanie pożeranego załatwia ewentualne pytania ,”po co ?”
Podobnie żelazne logiczne wydaje się wyrzygiwanie czegoś co się pożarło kilkadziesiąt lat temu a nawet przesadne głaskanie sarenki ..
” w jednej z gmin pod Częstochową nauczycielka geografii zabrała dzieci na wycieczkę, w polu znaleźli maleńką sarenkę. Zamiast odejść i zostawić zwierzę w spokoju, kilkanaście dziewczynek przez parę godzin głaskało tę sarenkę ”
Łatwo przewidzieć co myślała każda kolejna dziewczynka i nauczycielka
@wiesiek59
22 czerwca 2022
11:29
Sorry, ale nic nie poradzę na to, że kojarzysz mi się architektonicznie – z gargulcem czyli rzygaczem – ozdobnym zakończeniem rynny, którą leje się obfitym strumieniem woda spływająca z dachów dawnych budowli.
Po I swiatowej funkcjonowało co najmniej kilka tysięcy marek samochodowych.
Praktycznie każdy kraj uprzemysłowiony miał ich sporo.
Większość splajtowała, została przejęta, skonsolidowana.
Po II swiatowej ocalało kilkaset.
Obecnie jest ich kilkanaście, w tym nowe wypromowane przez Japonię, Koreę.
O markach chińskich czy indyjskich nie wiemy prawie nic.
Czy taka koncentracja w kilku blokach jest dobra czy zła, trudno powiedzieć.
Wyścig do kieszeni klienta to astronomiczne koszty na starcie każdego nowego modelu…
markot 22 CZERWCA 2022 11:50
A ty kojarzysz mi się z poprawnym politycznie wykszałciuchem, podobnie jak np. PAK4. 🙁
@olborski
sorry za „natachmiast”, mam klawiaturę qwertz 🙄 Powinno było wyjść „natuchmiast” 😉
Pechowa sarenka 🙁 Pewnie już ją wytropiły lisy albo okoliczne psy.
Czy nauczycielka biologii wiedziałaby lepiej?
kalvarya01,
trzech gosci przychodzi do hotelu.
Dowiaduja sie w recepcji, ze noc bedzie ich kosztowac razem $30. Placa takoz.
Po godzinie menedzer wola chlopca hotelowego: masz tu $5 i zwroc tym gosciom pod nr 12 – noc dzisiaj przeciez $25 za pokoj.
Sprytny callboy mysli: i tak nie podziela 5 bucks po rowno miedzy soba, wezme $2 dla siebie, dam im 3 do podzialu. Tak tez uczynil.
Goscie zadowoleni, ze wydali tylko po $9 na twarz.
3×9 +2 =29, gdzie podzialu sie ten dollar?!
Wiem, ze dosc dziecinne ale iluz ludzi nabiera sie na to!
podzial..
wiesiek59 22 CZERWCA 2022 11:55
W Polsce, po roku 1989, zbankrutowali albo zostali oddani za przysłowiowy grosz zagranicznym kapitalistom tacy producenci samochodów i maszyn „pokrewnych” jak FSO, FSM, Jelcz, Star, Fabryka Samochodów Rolniczych w Poznaniu, Fabryka Samochodów w Lublinie oraz fabryka traktorów URSUS. :-(
dacie rade bez googla w 5 minut?
F. Bronco Sport Big bend
bronco – a wild or half-tamed horse of the western US
– wysportowany półdziki a po’l ugłaskany koń mocno wygięty albo pochylony (nad żłobem a tnp wierzgający )
act 22 CZERWCA 2022 12:02
Za 30 „dolców”, to chyba tylko w najgorszych slumsach NYC czy Chicago. 🙁
Poza tym, to 2+3+25=30.
act 22 CZERWCA 2022 12:07
Mistsu-bishi Źrebak i Odważny – z pamięci… 😉
act 22 CZERWCA 2022 12:02
Pluskwy ich nie wyssały przez tą noc?
odpowiedz prawidlowa!
markot 22 CZERWCA 2022 12:01
Bardzo lubię lisy – bardziej niż sarenki ale mniej niż syrenki.
wole te druga, szybki jestes
@kalvarya01:
Kręcimy się w kółko.
> Chcę zwrócić Australię, Amerykę i Palestynę ich prawowitym właścicielom.
W odniesieniu do państw i narodów, mamy dwa sposoby uzasadniania:
– odniesienie do prawa naturalnego, czyli ziemia należy do tych, którzy ją zamieszkują;
– odniesienie do prawa historycznego, czyli ziemia należy do tych, którym dały je dawne traktaty, albo zasiedzenie sprzed czasów podziału granic.
Do którego z tych praw się odniesiesz w przypadku: Izraela, Krymu, Australii, Czeczenii, Kosowa, Doniecka, Kijowa? Bo widzę, że żonglujesz sobie tym zupełnie beztrosko, a tu se poprę bo tam mieszka dużo ludzi, a tu niech wrócą do granic z XVI wieku! Sorry, ale to jest wciąż argumentowanie, bo mam na to ochotę. Fakt, jeśli bym szukał jakiegoś dowodu kryzysu cywilizacji zachodniej, to właśnie triumf takiego sposobu dyskutowania, jaki prezentujesz, wskazałbym jako największy jej problem — wiarę, że jakieś widzimisię, czy inne muchy w nosie, mają moc prawną i dowodową.
> To dlaczego uważa się np. bojowników o wolność i jedność Irlandii, Baskonii czy Katalonii za terrorystów, więzi ich, prześladuje etc.?
A zrzuca na nich bomby, jak Rosjanie na Czeczenów, albo Putin na Ukrainę?
Tzn. owszem, zrzucano bomby na Basków. Myślę, że bardzo Cię cieszy, że uznaję fakt, iż Putin postępuje tak jak politycy tzw. „Zachodniej Europy”, a konkretnie Franco i Hitler.
> Jaki jest naukowy, czyli empiryczny dowód na to, że to nie Żydzi z carskiej Ochrany wyprodukowali te protokoły?
A ich tam przyjmowano do pracy? Gdybyś był Żydem na przełomie XIX/XX wieku, to w wielu krajach nie mógłbyś awansować na wrażliwe stanowisko państwowe.
> Tybet zawsze był częścią Chin
To zawsze jest tak samo prawdziwe jak stwierdzenie, że Polska zawsze była częścią Rosji. To bardzo podobny okres i zakres.
> Te „papiery z ONZ” były uzyskane drogą oszustwa,
Wydaje mi się, że Stalin wtedy przeliczył się z efektem jaki wywoła jego foch i wstrzymanie się od udziału w dyskusji.
To jednak pokazuje, co najczęściej blokuje takie wspólne, międzynarodowe działanie — protest imperium: Rosji, Chin, ewentualnie Stanów.
> inaczej to nikt by nie wyrzucał pieniędzy na wojsko.
Mam wrażenie, że im więcej działa prawa międzynarodowego, tym wydawany na wojsko odsetek PKB jest mniejszy. Hint: UE wydaje mniej niż Rosja.
Swoją drogą, ja bardzo lubię sprzęt wojskowy — świetnie się prezentuje w muzeach! Znam też miłośników parad.
> Co to znaczy, że USA miały Meksyk „na dłoni”? To tak samo, jakby powiedzieć, że Niemcy miały w roku 1939 Polskę „na dłoni”
Chodzi mi o wojnę z 1846-1848. Amerykanie serio stali przed wyborem, czy włączyć Meksyk do USA, czy nie.
> Śmieszny jesteś wstawiając Osetię Południową do tej samej przegródki co np. Monako, Bahamy albo Liechtenstein czy nawet Cypr Południowy („grecki”).
Proponuję się douczyć, gdzie się dzisiaj pierze pieniądze w Europie.
> W każdym stroju klasowym istnieje hierarchia społeczna. W Układzie Warszawskim i w RWPG, to Polska była numerem dwa, zaraz po ZSRR. W NATO i UE jesteśmy zaś, w najlepszym wypadku, dopiero gdzieś pod koniec pierwszej dziesiątki.
Lepiej być drugim na Sybirze, niż 10-tym w Kalifornii?
> Poza tym, to komunizm oznacza równość szans
Osz, kurcze, nie myślałem, że USA jest komunistyczne 😛
> A ty [markot] kojarzysz mi się z poprawnym politycznie wykszałciuchem, podobnie jak np. PAK4.
Ależ dziękuję! Dawno nie słyszałem tak miłego komplementu 😀
Morawiecki: NATO najsilniejszy sojusz w dziejach … Tak sobie myślę prywatnie … z ciupagami w Afganistanie nie miał mocy … nie był wyszczekany ….
Dlaczego katolicy nad Wisłą wolą zakładać polityczne partie zamiast prać brudy w kółkach różańcowych pod amboną … Tak sobie myślę prywatnie … bo to ambona trzepie parafianami … dwa trzepaki … w barszczu …
Zamiast zbroić banderowską Ukrainę aby żywiła świat … pieniądze na zbrojenia przeznaczyć na rolnictwo w krajach narażonych rzekomo na głód … Tak sobie myślę prywatnie … Abrams ciągnący agregat uprawowy … czy systemy nawadniania pól … a potem zalesić Saharę … po co kombinować …
SŁOWIANIN STANISŁAW
22 CZERWCA 2022
12:3
Bo partie polityczne otrzymują dotacje od hojnych sponsorów zza granicy….
To samo media, NGO. dziennikarze.
Tani sposób na zawłaszczenie kraju przez obce interesy.
@Wiesiek59:
> Bo partie polityczne otrzymują dotacje od hojnych sponsorów zza granicy….
To samo media, NGO. dziennikarze.
> hulają brytyjscy agenci i politycy, chcący miejscowych Słowian rzucać przeciw
A nie widzisz tu sprzeczności? Cytujesz Polonię Christianę 24, rzecz założoną za obce pieniądze, inwestowane w Polsce w interesie politycznym. I to Ci nie przeszkadza.
Cytuje Sakera, na którym wisi bardzo poważne oskarżenie o bycie rosyjską agenturą, manipulującą także miejscowymi Słowianami — i znowu, to Ci nie przeszkadza.
Przeszkadzają za to jakieś widma, których nikt nie dowiódł…
@STANISŁAW SŁOWIANIN:
> Dlaczego katolicy nad Wisłą wolą zakładać polityczne partie zamiast prać brudy w kółkach różańcowych pod amboną
Ale do czego przepijasz, skoro nad Wisłą jest dużo więcej kółek różańcowych niż partii politycznych?
SŁOWIANIN STANISŁAW 22 czerwca 2022 12:52
Podobno pod piaskami Sahary jest podziemne morze o pojemności większej niż Bałtyk. Wiedział o tym Kadafi i rozpoczął prace nad dostępem do niej i przesłaniem na tereny Afryki Północnej. Ale zamierzał zrobić coś o wiele „gorszego” – wprowadzić własną walutę rezygnując z dolara i funta.
Z tego powodu go zniszczono ale czy musiano także zniszczyć tę instalację ?
PAK4 22 CZERWCA 2022 12:20
1. Tak, kręcimy się w kółko, bo ty wciąż powtarzasz kłamstwa aktualnej oficjalnej linii reżimowej propagandy – tak jak dawniej i dziś lektorzy z Polskiego Radia, Telewizji i KC (dawniej PZPR, dziś POPiS-u).
Ziemia należy zaś do tych, którzy są jej prawowitymi właścicielami, a nie do tych, którzy ją zajęli siłą albo podstępem i usunęli z niej jej prawowitych właścicieli. W Ameryce i Afryce należy więc wrócić do granic sprzed zachodnioeuropejskiej inwazji. I nie mam nic przeciwko temu, aby Krym czyli Tauryda była grecka.
2. A mój sposób dyskutowania to jest typowa erystyka – znana zarówno w Europie jak i w Azji.
3. Może nie bomby, ale traktuje się ich kulami, aby nie zniszczyć infrastruktury, która należy do okupantów. Putin postępuje tak jak politycy tzw. „Zachodniej Europy” – tak jak np. Churchill, Adenauer, Mussolini, Salazar a nawet i de Gaulle…
4. Tak, ale ty nigdy nie pracowałeś w tego typu instytucjach… Zresztą Żydzi zawsze kolaborowali z okupantem: https://www.academia.edu/49449142/Kolaboracja_żydowska_w_III_Rzeszy_i_państwach_przez_nią_okupowanych
5. Raczej jak stwierdzenie, że Mazowsze zawsze było częścią Polski.
6. Tak czy inaczej, to USA napadły by wtedy na Koreę, tak samo jak nieco później napadły na Wietnam czy Kubę.
7. UE, tak jak Japonia, jest de facto wasalem USA a więc liczą te państwa czy ich zgrupowania na militarną pomoc ze strony swego Overlorda zza Wielkiej Wody. Swoją drogą, ja bardzo NIE lubię sprzętu wojskowego – może dlatego, że służba w LWP zabrała mi 4 lata mego życia, chociaż przyznaję, że sporo się podczas niej nauczyłem, ale nie zawsze tego, czego mnie ci wojskowi instruktorzy chcieli nauczyć.
8, W roku 1939 Hitler też na serio stanął przed wyborem: czy włączyć całą Polskę do Niemiec, czy też nie i wybrał rozwiązanie z GG. Rosja też nie od razu dołączyła Polskę do swego obszaru, vide np. Królestwo Kongresowe z osobną walutą, skarbem, wojskiem etc.
9. Ile tych pieniędzy ostatnio przeprałeś w Osetii Południowej (czyli Alanii), której przecież nikt na Zachodzie nie uznaje, chyba że uważasz Nikaraguę, Wenezuelę i Nauru za „Zachód”? Chyba, że to były ruble…
10. Tak, szczególnie, że Kalifornia pogrążona jest od lat w głębokim kryzysie zadłużenia, bezdomności, narkomanii, nieudolności policji etc. I czy ty naprawdę wierzysz w to, że córka bezdomnej, bezrobotnej i samotnej Murzynki ze slumsów np. Chicago albo Detroit City oraz syn miliarderów z bogatych przedmieść NYC czy LA mają w USA tak samo wielkie szanse?
Szalom!
PAK4 22 CZERWCA 2022 13:04
Czy wiesz, że nad tobą wisi bardzo poważne oskarżenie o bycie jankeską agenturą, manipulującą także tutejszymi Słowianami?
SŁOWIANIN STANISŁAW 22 CZERWCA 2022 12:52
W interesie Wielkiego Zachodniego Kapitału NIE leży to, aby pieniądze idące dziś na zbrojenia przeznaczyć na rolnictwo w krajach narażonych na głód.
Czytając ale nie pożerając , felietony nie wymagające komentarzy …
………………………….
„Jednak niebezpieczni dla polskich dzieci i polskiego dziedzictwa są sami Polacy – zaślepieni strażnicy „wolnego rynku”, którzy fundują masowe egzekucje małym księgarniom. Po Badecie powinna być tablica „W tym rejonie walczyły o polskie dzieci nieustraszone edukatorki, animatorki pod dowództwem kapitanki Anny. Poległy w bratobójczej walce. Cześć i chwała obrończyniom przyczółka Badet”. ”
……………
Przypominając sobie po przeczytaniu dawno , przed trzydziestu laty , umarły
przyczółek Bedet „zastanawiamy sie ” .. czego to był przyczółek ..(?)
Przyczółek ” Lesia ” , – chyba najbardziej
@kaesjot
Skąd masz informacje, że libijskie instalacje czerpiące wodę spod Sahary zostały zniszczone?
Z tego, co wiem, rurociągi nadal zaopatrują Trypolis, Bengazi i inne miasta na północy Libii, a także libijskie rolnictwo w wodę w ilości wielu milionów metrów sześciennych dziennie.
Kto leciał samolotem nad Saharą, widział pewnie te tajemnicze kręgi
Takie rolnictwo też nie jest bezproblemowe, bo nawadnianie powoduje wzrost zasolenia gruntu.
Woda pod Saharą znajduje się na głębokości 50-150 m. Są to wody reliktowe o wieku 30 000 – 100 000 lat i ich zasób nie odnowi się w ciągu naszego życia.
Przy aktualnej eksploatacji zasoby te mogą się wyczerpać już za 250 lat.
Przetłumaczcie to sobie:
China supercomputer achieves global first with ‘brain-scale’ AI model.
Research team says latest Sunway machine is on a par with the US Frontier, named as the world’s most powerful just weeks earlier
Its speed has made it possible to train an artificial intelligence program with 174 trillion parameters, rivalling the synapses in the human brain
South China Morning Post
Dla mniej „kumatych” po polskiemu:
Chiński superkomputer osiąga pierwszy wynik na świecie dzięki modelowi sztucznej inteligencji na skalę mózgu. Zespół badawczy twierdzi, że najnowsza maszyna Sunway dorównuje amerykańskiemu Frontierowi, który kilka tygodni wcześniej został uznany za najpotężniejszy na świecie. Jego szybkość umożliwiła wytrenowanie programu sztucznej inteligencji o 174 trylionach parametrów, co dorównuje liczbie synaps w ludzkim mózgu.
To pewnie za tydzien, za miesiac, najdalej za rok
osiagnie samoswiadomosc, kurde.
@markot
Takie rolnictwo też nie jest bezproblemowe, bo nawadnianie powoduje wzrost zasolenia gruntu.
Właśnie, przypomniało mi się, jak pewien białkowiec opowiadał (ze 30 lat temu) o jakiejś subtelnej różnicy między starożytnymi technikami nawadniania w Egipcie i Mezopotamii (w obu okolicach używano wody rzecznej). Samej różnicy nie pamiętam, ale przy metodzie stosowanej w międzyrzeczu zasolenie postępowało jakoby znacznie szybciej. Ciekawe czy to prawda.
A koncept liczb rzeczywistych wydaje mi się… naturalny, nawet jeżeli liczby rzeczywiste są zbędne.
PAK4
22 CZERWCA 2022
13:04
Mogę ci w nieskończoność cytować zachodnie doktryny polityczne, raporty think- tanków, wypowiedzi polityków, książki wydane przez byłych prominentów.
Masz tam czarno na białym opisane cele, metody, środki stosowane do ich osiągnięcia.
Ty zas powtarzasz papkę propagandową przeznaczoną dla proli.
NIC SIĘ NIE ZGADZA z rzeczywistością.
Jedyne w miarę trzeźwe spojrzenie na świat i kłębiące się w nim interesy, mają niestety polscy konserwatyści i marginalne grupy izolowane na scenie politycznej.
Resztę ogarnął amok, generowana psychoza, są na haju zaslepieni własną ideologią i nienawiścią.
Co do historii,
Niektóre mocarstwa pogodziły się z klęską.
Węgry, Austria, Niemcy, Hiszpania, Portugalia- na przykład.
Polska dalej odczuwa bule fantomowe po przegranej walce o prymat.
O sukcesie czy klesce decydują czesto nietrafne decyzje jednego człowieka.
My mieliśmy pecha….
Najzręczniej Wielką Grę o światowy prymat rozegrali Anglicy i ich amerykańscy spadkobiercy.
Ale nawet oni właśnie doszli do kresu swojej potęgi.
Napuszczając na sebie mocarstwa kontynentalne, prowokując wyniszczające wojny, spowodowali śmierć setek milionów ludzi na świecie.
Po co?
Władza jest tak pociagająca dla niektórych?
Teraz wykrwawiają Ukrainę.
Los wdów i sierot ich nie interesuje.
Poczytaj wypowiedzi brytyjskich polityków, generałów, z ostatnich miesięcy.
Może zorientujesz się w końcu w geopolitycznych rozgrywkach.
markot
22 CZERWCA 2022
13:53
Wybuchy kilkunastu tysięcy bomb i rakiet, spowodowały drgania gruntu niszcząc sieć rurociągów , zniszczeniu uległy przepompownie, pompy głebinowe, źródła zasilania.
Kadra techniczna konserwująca ten układ wyemigrowała.
Albo- jak 30 000 Chińczyków- została ewakuowana.
Siewcy Chaosu powinni być dumni ze swych osiągnięć w destrukcji kraju.
Gammon No.82 22 CZERWCA 2022 14:17
Wszystkie liczby to tylko abstrakcja, a więc istnieją one tylko w mózgach tych, którzy ich używają.
@Gammon No.82:
Hm… o Egipcie piszą, ale co z Mezopotamią? Basenów nie mieli?
https://www.histurion.pl/historia/starozytnosc/egipt/poczatki_cywilizacji_starozytnego_egiptu.html
@kalvarya01:
> Czy wiesz, że nad tobą wisi bardzo poważne oskarżenie o bycie jankeską agenturą, manipulującą także tutejszymi Słowianami?
Czy myślisz, że ja o Sakerze i o PCh24 pisałem tak sobie? W przypadku Sakera oskarżenie o agenturę rosyjską wysunął szwajcarski Czerwony Krzyż. W przypadku PCh24 też dokumentowano powiązania w publikacjach. Twoja reakcja jest, natomiast, kolejną próbą odbijania piłeczki.
> ty wciąż powtarzasz kłamstwa
Chciałem Cię prosić o przykład. Ale nie wiem, czy to ma sens, bo dla Ciebie prawdą jest to, co chwilowo za nią uważasz, a reżimowym kłamstw, amerykańską propagandą, ewentualnie jakimś błędem w poznawaniu świata, typu myleniem korelacji z przyczynowością, wszystko co Tobie nie pasuje. A jak pytam o dowody i argumenty, to jest wykpiwanie się.
> A mój sposób dyskutowania to jest typowa erystyka – znana zarówno w Europie jak i w Azji.
Primo, mówiłem o sposobie myślenia.
Secundo, tak, czytałem tego Polaka z Pomorza, Schopenhauer mu było 😉 Tylko on to pisał jako podręcznik obrony przed nieuczciwą argumentacją, a nie zachętę do nieuczciwości na co dzień.
> Raczej jak stwierdzenie, że Mazowsze zawsze było częścią Polski.
Znowu to Mazowsze? A nie wolałbyś czegoś oryginalnego typu: „Jak stwierdzenie, że Pomorze było zawsze częścią Szwecji”?
> Tak czy inaczej, to USA napadły by wtedy na Koreę, tak samo jak nieco później napadły na Wietnam czy Kubę.
Czyli co, 3 napady USA na zdławienie powstań w Berlinie, Budapeszcie, Pradze oraz zajęcie Kabulu? 😀 Nawet przyjmując Twoje wydumane interpretacje, to USA wypadają bardziej przyjaźnie i pokojowo 😀
> W roku 1939 Hitler też na serio stanął przed wyborem: czy włączyć całą Polskę do Niemiec, czy też nie i wybrał rozwiązanie z GG.
Tak, to niezła analogia. Tu i tu grał zresztą rolę rasizm.
> Rosja też nie od razu dołączyła Polskę do swego obszaru, vide np. Królestwo Kongresowe z osobną walutą, skarbem, wojskiem etc.
No, ale Królestwo Kongresowe było po Kongresie Wiedeńskim, czyli po Napoleonie, a nie po rozbiorach. Bo tak, Rosja od razu zajęła Polskę po rozbiorach.
> Ile tych pieniędzy ostatnio przeprałeś w Osetii Południowej (czyli Alanii), której przecież nikt na Zachodzie nie uznaje
Ale Wschód potrafi uznać. Transferuje się tak dochody z Donbasu, proszę Interlokutora.
> Tak, szczególnie, że Kalifornia pogrążona jest od lat w głębokim kryzysie zadłużenia, bezdomności, narkomanii, nieudolności policji etc.
Chcesz powiedzieć, że coś jak Rosja? Chociaż nie — Rosja nie ma kryzysu zadłużenia, za to Kalifornia nie ma kryzysu demograficznego.
> I czy ty naprawdę wierzysz w to, że córka bezdomnej, bezrobotnej i samotnej Murzynki ze slumsów np. Chicago albo Detroit City oraz syn miliarderów z bogatych przedmieść NYC czy LA mają w USA tak samo wielkie szanse?
Właśnie dlatego bawi mnie ta Twoja „równość szans”, jako podstawa komunizmu. Realna równość wymaga wielu działań afirmatywnych, których tu jawisz się jako głęboki przeciwnik. W tym analiz wypływających z nauk genderowych, czy afirmacji środowisk LGBT. A jak je odejmiemy, to mamy taką równość na papierze.
@wiesiek59:
> Mogę ci w nieskończoność cytować
Hm… alef zero, czy continuum? 😉
> Masz tam czarno na białym opisane cele, metody, środki stosowane do ich osiągnięcia.
No właśnie mam. I dlatego nie pasuje mi to, co twierdzisz.
Bierzesz część rzeczywistości (bardzo wybiórczą) za całość.
Po pierwsze, tak, na Zachodzie są żywe bardzo egoistyczne ruchy polityczne — w tle akurat sobie czytałem Rordika o „ciężkich czasach amerykańskiego triumfalizmu” — odwołujące się do czystej siły i poczucia własnej wyższości. Ale stanowią one tylko część myśli politycznej Zachodu. Znajdą się politycy oddani takim wizjom w całości, by przypomnieć Trumpa. Ale znajdą się i tacy, którzy będą próbowali opierać ład na uzgodnieniach międzynarodowych, opierać się na wartościach itp. Z tych samych USA — to była bardzo ważna myśl w działaniu Cartera i całkiem istotna u Obamy.
I teraz zapytam, co jest po drugiej stronie? Czy putinizm, albo obecna polityka chińska, w ogóle, w jakiejkolwiek mierze biorą pod uwagę wartości praw człowieka, demokracji, międzynarodowego porządku prawnego? Bo ja tam widzę tylko to, co jest złe w polityce zachodniej, a nie widzę tego, co w tej polityce zachodniej jest dobre.
Po drugie, mam wielkie wątpliwości co do Twoich odczytań. Zresztą nie tylko Twoich, bo dopiero co kalvarya mi tłumaczył, że lobbing to przekupstwo. Też tłumaczyłeś miliardy na demokrację w Ukrainie na kupowanie polityków i instalowanie premiera. To tak jakbym powiedział, że poszedłem do sklepu i przyniosłem — a poszalejmy sobie — masło. Na co Ty byś odpowiedział, że mogłem ukraść dwie kostki. Innymi słowy: sama informacja jest często neutralna, jak się zna lepiej te techniki, to się wie, że tam wiele działań jest „fajnych” i realnie dobrych (ocierałem się o rzeczy finansowane przez Sorosa w Polsce i tam nie było nachalnej propagandy politycznej, tylko bardzo fajne wspieranie ludzi i organizacji). Jeśli finansowania amerykańskie w USA były takiej jak w Polsce, to pieniądze szły na szkolenia (z realną wiedzą, a nie propagandą), wydawnictwa, stypendia, wyposażenia placówek szkolnych itp. Ale Ty dodajesz możliwie złośliwą, karykaturalną interpretację, no bo jakże to… To tak jak u tych paleo-kosnerwatystów (ależ mi Herstoryk zapewnił konika ;D ) — oni wieżą w nagą siłę i prawo dżungli, doszukują się go, interpretują w tym duchu, zamykają oczy na całą resztę. No i wychodzi im naga siła. To taki samonapędzający się mechanizm.
I, jak wyżej, jak usłyszałbym, że podobne pieniądze wydał Putin na „demokrację” gdzieś, to bym wątpił czy to poszło na realne szkolenia. Tam raczej, podejrzliwość w Twoim stylu, byłaby słuszna bo znowu — ten polityczny Wschód bierze to, co mu wygodne do rozpychania się zgodnego z prawem dżungli.
> polscy konserwatyści
Nie tylko polscy. To rozumienie polityki jako prawa dżungli jest w ogóle domeną konserwatystów. Zresztą trudno uznać to za przypadek — to jest mentalne tkwienie w czasach sprzed deklaracji praw człowieka i obywatela 😀 OK, wyzłośliwiam się, w końcu nawet w XVIII wieku, czy wcześniej, istniało pewne prawo międzynarodowe i trafiały się przypadki, że je egzekwowano. Więc konserwatyści tkwią w przeszłości wyimaginowanej, a nie realnej; a sugerować, że mają poglądy ze średniowiecza, byłoby dla średniowiecza krzywdzące.
> Węgry, Austria, Niemcy, Hiszpania, Portugalia- na przykład.
Węgry ewidentnie nie. Tęsknoty do rewizji Trianon są jednym z głównych paliw politycznych Orbana, zresztą łączą go z Putinem, jako dającym szanse na nowe rozdanie kart w Europie.
> Polska dalej odczuwa bule fantomowe po przegranej walce o prymat.
No właśnie powiedziałbym, że Polska jest bardzo pozytywnym przykładem. Oczywiście nie cała. Nie polscy konserwatyści 😀 Nie PiS. Nie Konfederacja. Ale generalnie, bóle fantomowe i np. rozpamiętywanie Wołynia, to przeszłość i margines.
> Ale nawet oni właśnie doszli do kresu swojej potęgi.
Dawno się uczyłem rosyjskiego, może coś przekręcę, ale powiedziałbym pożywiom, uwidim.
Piszesz o pewniku o czym, co ja bym uznał za niepewność. Więcej, gdybym musiał obstawiać u jakiegoś bukmachera, to chyba jednak postawiłbym na Zachód, jako mający wciąż więcej atutów i szans.
> Napuszczając na sebie mocarstwa kontynentalne, prowokując wyniszczające wojny
Jakieś przykłady?
OK, Wielka Brytania montowała koalicje przeciwko Napoleonowi. Nie jest to moja ulubiona epoka, nie znam się, może kogoś wtedy napuszczała. Ale największy jej rozkwit to wiek XIX, gdy po Napoleonie nie było jakiś wielkich wojen, przynajmniej nie takich, gdzie można mówić o „napuszczaniu mocarstw”. Zaś początek I wojny światowej jest nieźle opisany, owszem, dyskutowany, ale nie spotkałem ani jednego wyjaśnienia, które zrzucałoby winę na brytyjskie manipulacje. No i zapewniam — Hitler nie był brytyjskim agentem.
> Po co?
Wiesz, naczytałem się trochę o tej dawnej dominacji Royal Navy, co dzisiaj przypomina trochę militarną dominację USA. I, w zasadzie, co w tym złego? RN zapewniała wolny handel, owszem, promujący wtedy Wielką Brytanię. Tyle, że handel był na prawdę wolny, dawał szanse innym, a przeciwnikiem nie były (tak w ogólności, pomijając wojny opiumowe), jakiś protekcjonizm, czy próba ekonomicznej rywalizacji ze strony tego, czy owego państwa, ale zwykli piraci. Królowa Wiktoria opłacała niejako światową policję do walki z przestępcami. Czy to takie złe? Jak dla mnie to o wiele lepsze, niż napadanie na sąsiedni kraj, by przejść do podręczników historii jako zdobywca i jednoczyciel ruskich ziem.
> Teraz wykrwawiają Ukrainę.
To Putin ją napadł. Napadł w imię urojonych celów. Nie napadł Donbasu — napadł cały kraj, chciał opanować Kijów. To on ją wykrwawia.
I dodam jedno — na Putinie najwięcej straci zapewne nie Ukraina, ale sama Rosja.
Gammon no. 82,
jedyne, co jest ‚naturalne’ w liczbach (i calej matematyce) to… abstrakcja.
Co tam liczby rzeczywiste, wez ich podzbior – liczby tzw. naturalne.
1 lis + 1 kura = 2 czego? 1Kg pierza +1Kg maki = 2 Kg… robi sie jakos glupio. 2 elektrony + 2 galaktyki.. jeszcze glupiej. 2 + 2 = 4, to juz nie tak glupio ale co to znaczy? Wszystko inne, cala matematyka jest konsekwencja tej naszej zdolnosci do abstrahowania.
Kiedy wezmiesz np. tak wyemancypowana liczbe 3, to juz mozesz robic z nia cuda, ze ona ‚trzecia, liczac od jednosci, ze nieparzysta, ze jednak pierwsza, bo ‚prime’ 🙂 etc. etc.
Pytanie, na ktore nie znam odpowiedzi, to skad te byty abstrakcyjne biora sie w naszych umyslach.
Nawet Penrose kapituluje niejako umieszczajac je po platonsku miedzy swiadomoscia a fizykalna rzeczywistoscia. Czym jest ta trzecia domena, Bog raczy widziec albo sam Platon.
A jednak 5 zlotych lepiej miec niz 3, a liczby urojone przydaja sie w budowie mostow i to jest dopiero jajo.
Pani zwazy cztery jablka (4 to 4 choc kazde jablko inne).
kalvarya01,
dopiero po napisaniu swojego widze Twoj wpis.
Ale skad sie w tych mozgach sie wziely, oto pytanie.
act 22 CZERWCA 2022 14:08
To może on, tak jak u Lema w ”Go-Lemie” połączy się on z innymi komputerami i zabroni im współpracy z wojskowymi, aby wojny mogły być toczone tylko, jak to przewidział sam Einstein, jedynie przy pomocy kijów i kamieni? Może to nauczy czegoś militarystów typu PAK4?
@Gammon No.82
Z jednego z sumeryjskich mitów założycielskich wynika ponoć, że klimat Mezopotamii sprzed 5 tys. lat, choć półpustynny, nie wymagał stałego nawadniania pól. Wykorzystywano raczej zatrzymywanie wód deszczowych przy pomocy zapór i systemu cystern, i nawadnianie niżej położonych terenów przez zalewanie pól położonych terasowo, a po infiltracji i podniesieniu poziomu wód gruntowych uzyskiwanie co najmniej jednego zbioru.
Po metody zatrzymywania wód opadowych ludzkość sięgała już bardzo wcześnie, a
ślady po antycznych zaporach zachowały się np. w Beludżystanie, Jemenie, Jordanii, Egipcie… Hetyci byli podobno pierwszymi, którzy zaczęli uszczelniać kamienne zapory gliną.
Ślady po kanałach i lokalnych rowach odprowadzających zatarły się z biegiem czasu, ale hipotezy wczesnej gospodarki wodnej znajdują coraz więcej uznania wśród archeologów, choć nie udaje się ustalić jej początków. Dobrze udokumentowana jest na przykład budowa kanału poprawiającego zaopatrzenie w wodę asyryjskiej Niniwy, ale to już czas późniejszy, ca 700 BC.
Dziś sposoby gromadzenia i wykorzystania deszczówki nazywają się rainwater harvesting i przeżywają swój renesans wokół basenu Morza Śródziemnego.
Większość domów ma tam zamiast dachu coś w rodzaju basenu z odprowadzeniem do cysterny w piwnicy, gdzie podczas pory deszczowej gromadzi się zapas wody na czas letniej suszy.
Widziałem to też w Ugandzie i okolicach.
Sam praktykuję zbieranie deszczówki do beczek i podlewanie nią ogrodu.
O regionalnych różnicach w problemach z zasoleniem gleb w czasach antycznych nie mam pojęcia. Pewnie zależało od intensywności nawadniania i np. dwóch zbiorów zamiast jednego. Nawadniając pustynię na okrągło można dziś uzyskać trzy sezony uprawne, więc i zasolenie wzrasta szybciej.
Ktory to Golem? Golem IV?
A LEM to Law of Exluded Middle, przestrzegasz?
Excluded…
Golem XIV….
PAK4 22 CZERWCA 2022 15:14
1. Cała tzw. myśl polityczna tzw. Zachodu opiera się na błędnym założeniu wyższości tzw. Zachodu nad resztą świata, czyli jest ona fundamentalnie rasistowska i szowinistyczna. Carter i Obama byli (są) głupkami, wylasowanymi przez elity z NYC. Obaj byli też (są) zbrodniarzami wojennymi. Prawa człowieka, demokracja, międzynarodowy porządek prawny etc. wedlug USA to jest uznanie nielegalnej okupacji Palestyny przez Chazarów, łamanie praw człowieka w Arabii Saudyjskiej i prowadzenie zaborczych wojen przez NATO.
2. Lobbing to jest legalne przekupstwo, tak samo jak giełda jest legalnym kasynem. Inna nazwa dla tego samego.
3. Soros jest zwyczajnym złodziejem i oszustem.
4. W realnej polityce liczy się tylko siła.
5. W polityce obowiązuje prawo dżungli – mówię ci to jak m. in. posiadacz PhD z nauk politycznych (Monash).
6. Sprawców zbrodni na Wołyniu wciąż nie rozliczono, a na Ukrainie stawia się im pomniki.
7. Zachód to jest przeszłość, przyszłość to jet Wschód.
8. Rozklwit UK polegał na napadaniu na kolejne państwa. Brytyjczycy to jest naród zbrodniarzy, tak jak np. Belgowie czy Francuzi.
9. Hitler był agentem Wielkiego Zachodniego Kapitału i Watykanu.
10. Pax Britannica polegał na tym, że wolny handel morski ograniczony był do UK i jego posiadłości. Wojen opiumowych NIE można zaś pomijać! A Putin tak samo napadł na Ukrainę jak Piłsudski w roku 1920. Ukraina jest zaś od dawna państwem upadłym – https://www.academia.edu/57162621/A_note_on_the_economic_collapse_of_Ukraine_in_years_1990_2020.
tak, wiesiek, dzieki, dawno temu czytalem
act 22 CZERWCA 2022 15:28
Wiadomo, że XIV. Poza tym: „Nikt nie czyta; jeśli czyta, nic nie rozumie; jeśli nawet rozumie, natychmiast zapomina” (prawo Lema).
22 CZERWCA 2022 15:17
Gdybym to wiedział, to byłym Panem Tego Świata równym JHWH i samym Diabłom.
Shalom!
@ ej-si-ti: No. I do NOT obey the so called Law of Exluded Middle. 😉
PAK4
22 CZERWCA 2022
15:14
Od 1945 roku 300 zamachów stanu, 50 większych konfliktów militarnych z udziałem żołnierzy USA.
Nie liczę Francji i GB, trudno policzalne interwencje w Afryce.
Ustaw sobie Koreę, Algierię, Wietnam, Egipt, Grecję, naprzeciw interwencji rosyjskiej na Wegrzech.
Może coś do ciebie dotrze.
Albo, Doktrynę Monroe, Powstrzymywania, naprzeciw Doktryny Breżniewa.
I skutki tychże.
Żarliwy z ciebie neofita, bez głębszej wiedzy o świecie.
Demokracja jest wymysłem zachodu.
Nie jest to szczyt osiągnięć ludzkości.
Po prostu, tylko na tyle intelektualistów zachodnich było stać.
I byli na tyle silni, by narzucić tę koncepcję połowie świata będącej pod ich kontrolą.
Jako pożyteczne narzędzie budowania wpływów politycznych.
Finansowanie opozycji jest słuszne.
Pod warunkiem że ta opozycja nam służy- takie jest przeslanie.
Po to się ją finansuje, by mieć kundelki szczekające na rozkaz, nie dbające o dobro swego kraju.
To inwestycja w agentów wpływu, kompradorów.
Przerabialismy to już w I RP.
Zachód jest skończony ekonomicznie, moralnie, technologicznie, finansowo.
Jest trupem, tylko jeszcze elity o tym nie wiedzą.
Potrwa to jeszcze kilka- kilkanaście lat.
GÓRA.
Chciwość nielicznych zarżneła gospodarkę.
Bilans handlowy ujemny.
Wydatki wojskowe astronomiczne.
Koszty życia monstrualne.
Lenin miał rację.
Kapitalizm sprzedal sznur, na własną szyję, dla zysku.
https://dwagrosze.com/2022/06/eu-wraca-do-wegla/comment-page-1/?unapproved=55862&moderation-hash=89e3c4689ce70023517bd6ec756d7e2e#comment-55862
=========
Skrzecząca rzeczywistość dopadła fanatyków?
Epps-Johnson założyła CTCL w 2012 roku, gdy miała 20 lat. Do 2019 roku była w najlepszych ligach, kiedy Mark Zuckerberg z Facebooka i jego żona Priscilla Chan przekazali CTCL kilka darowizn o łącznej wartości ponad 419 milionów dolarów, aby wpłynąć na wybory w USA w 2020 roku. Jak to zostało zrobione, to studium wyrafinowanej i oczywiście nielegalnej manipulacji wyborami.
https://journal-neo.org/2022/06/08/zuckerberg-rockefeller-google-and-the-privatization-of-election-integrity/
==========
Pieniądze nie mają znaczenia.
Darczyńcy sa altruistami.
Kto uwierzy w takie bajki?
PAK4?/?
z nawadnianiem trzeba ostroznie
zasolenie to jedno, to chyba Kapuscinski opisal jak zniszczono stepy w kraju Voldomora? Prawdopodobnie wyjasnia to obecnosc przytrutych mentalnie Orkow.
inny przyklad
Linking Selenium Sources to Ecosystems: Irrigation
https://www.usgs.gov/mission-areas/water-resources/science/linking-selenium-sources-ecosystems-irrigation
przenikanie rteci i arszeniuku z hald odpadow elektocieplowniczych to kolejny …
Pozyskiwanie wody pitnej za pomoca reverse osmosis (RO), tez produkuje odpady.
W tym ostatnim przypadku troszeczke sie przyczynilem razem z corka aby zablokowac glupia inwestycje (RO) w miasteczku Marina w Kaliforni nad Monterey Bay.
W modelowaniu przeplywu stosowalem FEA, czyli taki rachunek rozniczkowy.
Jestem za wolnoscia slowa.
Dlatego proponuje zmiane nazwy na Blog Otwarty.
Ten blog ma niewiele wspolnego z nauka.
Slawomirski
Najciemniej nad Wisłą … co z terytorialnymi skutkami Jałty … sukces Gruzina … Tak sobie myślę prywatnie … czy hunwejbini nad Wisłą po unieważnieniu Jałty /tak Macierewicz/ oddadzą co zagrabione i odbiorą co zabrane …
Slawomirski
22 CZERWCA 2022
17:12
Mylisz się.
Nauką jest podobno historia i GEOPOLITYKA.
Bezpośrednio wpływająca na życie na Ziemi.
W tym i nasze- obecnie.
Dyskusja to wymiana poglądów, argumentów, punktów widzenia, interpretacji faktów, wymiana doświadczeń, wiedzy.
Masz coś przeciwko KULTURALNEJ DYSKUSJI?
Jesteś stary bywalec.
Na przestrzeni ostatnich kilkunastu lat zaszły kolosalne zmiany.
Dostrzegasz?
Nie ma Hyde Parku, jest Nowomowa i preferowanie zachowań stadnych, cenzura, ostracyzm, polowania z nagonką.
SŁOWIANIN STANISŁAW
22 CZERWCA 2022
17:18
Warunkiem uznania niepodległości Litwy i jej granic był wolny tranzyt do Kaliningradu.
Nowy punkt zapalny powstał.
Rozwiązanie?
Pociągi pancerne?
Gorbaczow ma chyba kaca moralnego … tak spieprzyć rozwiązanie ZSRR … Tak sobie myślę prywatnie … zapomniał o narodowym charakterze przyszłych terytoriów … a nie na podziale na republiki … dla divide et impera …
@markot 13:53
Takie tajemnicze kręgi widziałam lecąc z południa na północ nad zachodnimi stanami Ameryki. Tam od lat notowano wyczerpywanie się warstw wodonośnych.
To się nazywa „large-scale center-pivot spray irrigation system”.
Urządzenie nawadniające kręci się wokół osi jak wskazówka zegara i rozpyla wodę nad uprawami. Dawniej z jadącej po polu rury strzelało strugami wody we wszystkich kierunkach, co oznaczało szybsze nawadnianie, ale duże straty przy parowaniu, teraz raczej imituje się mżawkę.
Woda pochodzi ze studni i rurociągów.
Na nawadnianie upraw przeznacza się 80 proc. wszystkiej wody zużywanej w USA.
Slawomirski 22 CZERWCA 2022 17:12
Czytałeś może moje wpisy na temat np. estymatorów i AI? Co z nich zrozumiałeś?
Uprawa kukurydzy w Arizonie
markot 22 CZERWCA 2022 20:43
Tak czy inaczej, takie rolnictwo na pustyni nie ma sensu, chyba że podatnicy dotują tą wodę.
R.S. 22 CZERWCA 2022 16:58
Zasolenie gleby to jest od dawna prblem nr 1 rolnictwa Australii. Niebawem będą tam więc musieli importować zboże, gdyż ogromna większość obszaru tej największej wyspy świata po prostu NIE nadaje się jakiejkolwiek uprawy, może poza kaktusami, a co już dawno temu odkryli Aborygeni, ale co zachodnioeuropejscy najeźdźcy zlekceważyli w swej anglosaskiej bucie i głupocie.
I czy dane, które wykorzystałeś do swoich obliczeń maja charakter ciągły czy też dyskretny?
PAK4 22 CZERWCA 2022 14:43
1. A co na to Saker i np. Palestyński Czerwony Półksiężyc?
2. Ty nic nie piszesz od siebie, tylko powtarzasz to, co ci mówi reżimowa, polskojęzyczna propaganda.
3. To chcesz wprowadzić kontrolę myśli?
4. Na Mazowszu i Pomorzu żyli zawsze Słowianie, częściowo później zgermanizowani, ale Słowianie, a nie Germanie jak w Szwecji.
CDN
PAK4 22 CZERWCA 2022 14:43
5. Powstanie w Belinie było dziełem nazistów, podobnie jak w Budapeszcie. Pamiętaj, że Węgry były chyba jedynym sojusznikiem III Rzeszy, wiernym Hitlerowi do samego końca. Podobnie było z Czechami, ochoczo kolaborującymi z III Rzeszą.
Interwencje militarne USA po roku 1945:
1946 Filipiny – wsparcie prawicowego rządu w obliczu powstania ludowego.
1947 Grecja – wojskowe wsparcie logistyczne dla prawicowego reżimu rojalistycznego zaangażowanego w wojnę z narodem.
1950 do 1953 napad USA na Koreę.
1953 Iran – CIA organizuje zamach stanu w celu obalenia premiera Mohammada Mossadegha .
1954 Gwatemala – obalenie legalnego rządu.
1958 Indonezja – nieudane wsparcie dla prawicowych przeciwników prezydenta Sukarno.
1958 Liban – interwencja w ramach tzw. doktryny Eisenhowera (walka z komunizmem w tym regionie).
1960 Gwatemala – bombardowania.
1961 Kuba – niepowodzenie lądowania w Zatoce Świń przeciwników Fidela Castro.
1961 do 1972 Wietnam – wojna z narodem wietnamskim. Sierpień 1964: podczas gdy amerykańscy doradcy wojskowi są obecni w Wietnamie Południowym od dziesięciu lat, Prezydent Johnson przywołuje fikcyjny atak na dwa amerykańskie niszczyciele przez północnowietnamskie łodzie torpedowe (tzw. incydenty w Zatoce Tonkińskiej), prosząc Kongres o rezolucję wyrażającą determinację Stany Zjednoczone będą „wspierać wolność i chronić pokój w Azji Południowo-Wschodniej”. Przyjęta uchwała upoważnia prezydenta do użycia konwencjonalnych sił zbrojnych w Azji Południowo-Wschodniej bez oficjalnego wypowiedzenia wojny. Stany Zjednoczone angażują się następnie w otwarty konflikt, który potrwa do 1975 roku. Liczba amerykańskich żołnierzy rozmieszczonych w Wietnamie osiągnęła 543 000 w Kwiecień 1969. Wojna naznaczona była potężnymi protestami w Stanach Zjednoczonych i licznymi tam zbrodniami wojennymi.
18 marca 1969 – 26 maja 1970 Kambodża – Stany Zjednoczone prowadzą bombardowania (3,875 lotów bojowych i 108.000 ton bomb).
11 listopada 1968 – 29 marca 1972 : Operacja Commando Hunt , bombardowania Laosu i Wietnamu Północnego. Różne inne interwencje w Kambodży , Laosie i Wietnamie.
1964 Brazylia – poparcie dla obalenia João Goularta przez juntę wojskową, która ustanowiła dyktaturę w latach 1964-1985.
1964 Kongo – tajne wsparcie lotnicze dla władz lokalnych przeciwko partyzantce prowadzonej przez najemników, którzy staną się rdzeniem kongijskich sił powietrznych podczas kryzysu kongijskiego w Demokratycznej Republice Konga.
1965 Indonezja – poparcie sił prawicowych.
1965 Zajęcie Republiki Dominikany przez Stany Zjednoczone po interwencji w wojnie domowej przy wsparciu tzw. Organizacji Państw Amerykańskich.
1970 Kampania USA w Kambodży.
11 września 1973 Chile – pomoc przy przeprowadzeniu zamachu stanu przez generała Augusto Pinocheta.
1973 Transport lotniczy do Izraela podczas wojny Jom Kippur.
1979-1992: Afganistan – uzbrajanie przez CIA afgańskich terrorystów walczących przeciwko ZSRR.
1980 do 1990 Salvador -pomoc wojskowa dla rządu i dla szwadronów śmierci. 100 000 osób zginęło w tej wojnie domowej.
1981 do 1988 Nikaragua – wsparcie „contras” w walce z lewicowym rządem.
1983 Liban – interwencja w Bejrucie.
25 października 1983 – 15 grudnia 1983 Grenada – inwazja.
1986 14 kwietnia Libia – Operacja El Dorado Canyon, bombardowanie kilku ośrodków politycznych i baz wojskowych w Libii , 45 zabitych Libijczyków, dwóch amerykańskich pilotów zabitych w wyniku antyamerykańskich ataków w Europie.
Panama , 20 grudnia – inwazja Stanów Zjednoczonych na Panamę.
1991 Wojna w Zatoce Perskiej (operacja Pustynna Burza).
1992 – 1993 Somalia – operacja Restore Hope, interwencja wojskowa Stanów Zjednoczonych.
1994 Haiti – operacja celu ustanowienia prezydentem Jeana-Bertranda Aristide’a.
1995 Bośnia i Hercegowina – wsparcie lotnicze dla sił NATO.
1998 Irak , cztery dni bombardowania celów wojskowych i przemysłowych.
1998 20 sierpnia, podwójne bombardowanie fabryki leków w Sudanie i obozów szkoleniowych partyzantów w Afganistanie po atakach na ambasady amerykańskie w Afryce 7 sierpnia 1998.
1999 Bombardowania NATO w Federalnej Republice Jugosławii (marzec-czerwiec 1999) (Serbia, Czarnogóra, Kosowo). Bombardowanie NATO i interwencja naziemna podczas wojny w Kosowie, a od tego czasu rozmieszczenie tzw. sił pokojowych .
1999 Timor Wschodni – wsparcie logistyczne w celu odłączania tego obszaru od Indonezji.
2001 Tzw. wojna z terroryzmem zostaje wypowiedziana po atakach z 11 września 2001 roku.
2001 Interwencja USA w Afganistanie w ramach tej wojny.
2002: Filipiny – wsparcie dla prawicowego rządu Filipin przeciwko partyzantom.
2003 – 2011 wojna w Iraku , Stany Zjednoczone napadają na Irak przy wsparciu Wielkiej Brytanii i innych krajów bez porozumienia ONZ.
2004 Amerykańskie ataki lotnicze w Pakistanie w celu pomocy rządowi Pakistanu w kontekście konfliktu zbrojnego w północno-zachodnim Pakistanie.
2004 Haiti – Stany Zjednoczone, w ramach interwencji wojskowej i przy pomocy Francji; odsunięcie od władzy prezydenta Haiti Jean-Bertranda Aristide’a.
2006 -Bombardowanie z powietrza celów Al-Kaidy w Somalii.
2011 Interwencja wojskowa USA w Libii.
2014 do dziś wojna z Państwem Islamskim w Iraku i Syrii, bez zgody tego ostatniego.
2017 Pomoc sił specjalnych USA w bitwie z islamskimi powstańcami pod Marawi na Filipinach.
2017 Bombardowanie bazy lotniczej Al-Chaayrate.
2018 Bombardowania Barzé i Him Shinshar.
Wystarczy?
PAK4 22 CZERWCA 2022 14:43
6. Przed Napoleonem, to obecna, czyli „etniczna” Polska znajdowała się w zaborach Pruskim i Austriackim, a nie Rosyjskim.
7. Jaki to jest % pieniędzy pranych dziś przez tzw. Zachód?
8. Kalifornia ma też kryzys przeludnienia. Ludzie budują tam więc domy, a właściwie baraki mieszkalne, nawet w lasach, które się często palą.,
9. Realna równość wymaga zniesienia kapitalizmu, a nie tzw. działań afirmatywnych, które powodują, że preferuje się nie osoby kompetentne, ale mające „odpowiednią” rasę, płeć czy też orientację seksualną, a co rozkłada dziś tzw. Zachód na obie łopatki, pomijając, że jest to rasistowskie, seksistowskie i wręcz chore, gdyż nie ma też czegoś takiego jak „gender”. Są tylko dwie naturalne płcie: męska i żeńska oraz osobnicy chorzy, wymagający pomocy medycznej a nie „afirmacji”.
Coś o „bias”.
Myślę polskiemu czytelnikowi najlepiej wytłumaczyć to na przykładzie:
„1950 do 1953 napad USA na Koreę.”
Katolicyzm zgermanizował Słowian nad Wisłą … w ramach Świętego Cesarstwa Rzymskiego Narodu Niemieckiego … Tak sobie myślę prywatnie … efektem modlitwa o zdrowie papieża a nie tubylczego prezydenta …
@PAK4
Moje uwagi do: ACADEMIA Letters – THE WORLD BANK, COVID-19 AND GLOBALPRODUCTIVITY – REFERENCE PARADIGMS (Critical Assessment)
Daniel Linotte, St. Antony’s College, Oxford
(BANK ŚWIATOWY, COVID-19 I PRODUKTYWNOŚĆ GLOBALNA – PARADYGMATY REFERENCYJNE (ocena krytyczna))
Ta krytyczna ocena zwraca uwagę na luki w zakresie odpowiedzialności społecznej w raporcie Banku Światowego „Global Productivity – Trends, Drivers, and Policies” (Światowa produktywność – trendy, czynniki i polityka”). W artykule podkreślono brak troski o społeczny i ludzki dobrobyt. Wielu zachodnich ortodoksyjnych ekonomistów ma bowiem niefortunną tendencję do niezaangażowania się w ekonomię jako etyczną naukę społeczną, która zajmuje się życiem istot ludzkich, ale traktuje ją tak, jakby zajmowała się tylko „rzeczami” mierzonymi w pieniądzu. W związku z tym w raporcie Banku pominięto kwestie etyczne, rosnące nierówności majątkowe i rosnącą różnicę w zarobkach. Kwestie te są bardzo niepokojące i dlatego ważne jest, aby zawsze je podkreślać, gdy są pomijane przez ważnych uczestników życia społecznego, takich jak Bank Światowy.
@PAK4
Uważam też, że Covid został „wynaleziony” przez USA w celu sabotowania chińskiej gospodarki, ale był on używany w tak wadliwy sposób, że bardziej zaszkodził gospodarce amerykańskiej i ogólnie zachodniej niż gospodarce ChRL. Tak czy inaczej, obecnie jest to już niemodne i nawet bliscy sojusznicy (a raczej wasale) USA, tacy jak np. Polska, znoszą obecnie praktycznie wszystkie ograniczenia związane z Covid, gdyż wyrządziły one wiele szkód ich gospodarkom.
Jak też już to pisałem – zmiany klimatu nie są kwestią ekonomiczną, lecz fizyczną i bardzo trudno byłoby udowodnić, że działalność człowieka może je zmienić w inny sposób niż wywołanie globalnej wojny nuklearnej.
@PAK4
Należy też zauważyć, że ponad 80% PKB w tzw. krajach rozwiniętych stanowią usługi, a wiele z nich jest de facto bezwartościowych poza nimi (np. usługi świadczone w USA przez amerykańskich prawników, księgowych, maklerów giełdowych, doradców podatkowych itp.) Dlatego też PKB USA wydaje się być mocno zawyżony.
Ponadto w ostatniej dekadzie XX wieku wiele krajów zachodnich, a zwłaszcza USA, wprowadziło nową metodologię obliczania PKB, która jest niezgodna z metodami stosowanymi w pozostałych krajach świata. Polega ona na sztucznym zawyżaniu wartości niektórych dóbr, głównie tzw. wysokiej techniki (lub zaawansowanej technologii – po angielsku high tech), takich jak komputery i ich oprogramowanie, których ceny mnoży się przez arbitralnie ustalone przeliczniki (mnożniki), aby zrekompensować spadek ich cen, związany z postępem technicznym, a także na dodawaniu do PKB hipotetycznych czynszów, „zarabianych” przez ludzi mieszkających we własnych mieszkaniach (tzw. czynsze kalkulacyjne, po angielsku imputed rents). Nie chodzi tu głównie o poprawność tej metodologii, ale raczej o fakt, że nie każdy kraj stosuje te arbitralnie przyjęte mnożniki i uwzględnia fikcyjne dochody z nieistniejących czynszów, przez co PKB takich krajów (np. USA) jest sztucznie i arbitralnie zawyżany w stosunku do innych krajów, które nie stosują tych mnożników i nie dodają do PKB fikcyjnych dochodów z czynszów. Oficjalna nazwa tej metody to „Hedonic Methods for Quality Adjustment” („Hedoniczne metody korekty jakości” – patrz np. Stewart, K.J. & Reed, S. „Consumer Price Index research series using current methods” w „Monthly Labor Review”, czerwiec 1999).
@wiesiek59 & pieniądze, napaści i zmiany rządów:
Zarzucasz mi, że nie znam rzeczywistości, a dla mnie to Twoje podejście jest strasznym rzeczywistości uproszczeniem. Coś jakbyś zmuszał mnie do refleksji nad liczbami rzeczywistymi, a pokazywał, że nie znasz i nie rozumiesz ułamków.
Znalazłem inny przykład-porównanie. To tak jakbyś każdy seks uznawał za gwałt. I powiedzmy, że mówię, iż X zgwałcił Y i powinien trafić do więzienia (Rosja napadła Ukrainę i należy pomóc w każdy pokojowy* sposób, by ją stamtąd wykopać, a w ideale, postawić Putina przed trybunałem za zbrodnie wojenne); gdy Ty odpowiadasz, że przecież sąsiadka jest w ciąży, więc gwałt to normalna sprawa i wszyscy gwałcą (Zachód przeznacza pieniądze na „szerzenie demokracji”).
Mnie przy takich argumentach ciarki przechodzą. Bo nie tylko chodzi o zamykanie oczu na dużą część rzeczywistości, gubienie półcieni (a kto powiedział, że nie ma molestowania itp. albo że między agresją zbrojną, a finansowaniem wycieczek na zapoznanie się z dobrze funkcjonującym systemem samorządności, nie ma półcieni, możliwych nadużyć, wciskania się agend ideologicznych** itd.; albo kto powiedział, że sąsiad na pewno nigdy nikogo nie zgwałcił?), ale przede wszystkim normalizowanie zbrodni (cosi fan tutti). Ja mogę rozumieć paleo-konserwatystów, bo oni wciąż się zachowują jak ci jaskiniowcy z dowcipów, co to zdobywają kobiety maczugami, ale tak na serio w dyskusji?
*) Mam na myśli: bez ataku NATO na terytorium Rosji. Dostarczanie broni, amunicji, nawet ułatwienie w pozyskiwaniu i szkoleniu ochotników uznawałbym za dopuszczalne.
**) Takim serio przykładem było finansowanie w Polsce SKCh im. ks. P.Skargi, z jego agendami jak OI, przez darczyńców — z Rosji (zapewne Kremla), ale także z USA. Ale, tu wracamy na początek — jak dyskutować o półcieniach z ludźmi, którzy widzą tylko czerń?
@kalvarya01:
Nie mam czasu na głupoty i wymienianie „etnicznie polskich” miejscowości, które trafiły w ręce rosyjskie przed Napoleonem. Zaznaczę tylko, że ten straszny gender to angielskie słowo na oznaczenie rodzaju; i świetnie wiemy z języka polskiego, że rodzajów jest więcej niż dwa — oprócz męskiego i żeńskiego jest jeszcze nijaki — to w liczbie pojedynczej, bo w liczbie mnogiej pojawia się już męskoosobość i niemęskoosbowość. No chyba, że uważasz iż właśnie trzy gendery w języku polskim rozłożyły IRP na łopatki i wymusiły bratnią pomoc Rosjan pod wodzą Niemki?
@PAK4 22 czerwca 2022 15:14
To tak jak u tych paleo-konserwatystów (ależ mi Herstoryk zapewnił konika ;D ) — oni wieżą w nagą siłę i prawo dżungli, doszukują się go, interpretują w tym duchu, zamykają oczy na całą resztę. No i wychodzi im naga siła.
Jeśli paleo-konserwatyści w cokolwiek wierzą, to w polityczny realizm, czyli stosowanie siły, i to niekoniecznie nagiej, tylko jeśli jest to naprawdę niezbędne.
Ja tam żadnym konikiem nie jestem, staram się, raczej jak pszczółka, zbierać nektar (jeśli sensowny i racjonalny) z różnych kwiatków, nawet pale-konserwatywnych, żeby sklecić jakiś zdrowy miód opinii.
@PAK4
Ponadto, to według ONZ-u, PKB oznacza jedynie produkcję tych dóbr i usług, które są sprzedawane na rynku. Wśród tych dóbr i usług są nie tylko te, które poprawiają dobrobyt i dobrostan ludności danego kraju, ale także te, które ten dobrobyt i dobrostan po prostu zmniejszają. PKB mierzy też usługi rządowe po kosztach (a więc je zaniża) i nie obejmuje tej części produkcji rolnej, która pozostaje w gospodarstwie (co zaniża PKB mniej rozwiniętych państw) i nie obejmuje produkcji gospodarstw domowych, zwłaszcza produkowanej przez kobiety, ponieważ do PKB wlicza się tylko to, co jest sprzedawane, a w praktyce to przecież nie jest wszystko. PKB jest więc seksistowski, ale „genderowcy” tacy jak np. @PAK4 po prostu NIE chcą tego zauważyć.
Produkcja sektora nieformalnego, spora szczególnie w krajach mniej rozwiniętych też nie jest (na ogół) w ogóle wliczana do PKB – rasistowska dyskryminacja tzw. III świata. Ogólne dane na temat całkowitego PKB i jego średniej czyli „na głowę mieszkańca” nie dostarczają też żadnych informacji na temat podziału dochodów i korzyści ekonomicznych dla różnych grup społecznych, które mogą one uzyskać w wyniku rozwoju gospodarczego. PKB nie mówi też nic o warunkach pracy i satysfakcji z niej czerpanej; nie mówi też nic o poziomie uczestnictwa w życiu narodowym różnych grup społecznych i nie mówi nic o innych ważnych wymiarach rozwoju, takich jak sytuacja demograficzna i warunki polityczne.
Porównania międzynarodowe często zawodzą także ze względu na fakt, że kursy walutowe nie nadają się do określania względnej siły nabywczej walut, zwłaszcza w dziedzinie konsumpcji dóbr i usług przez gospodarstwa domowe. Badania alternatywnych metod porównywania PKB między krajami, opartych na sile nabywczej walut, wskazują, że konwencjonalne przeliczanie walut (czyli według kursu wymiany) może wyolbrzymiać względny dystans ekonomiczny między krajami o wysokim i niskim PKB na mieszkańca (per capita). Dobrze ilustruje to fakt, że nikt nie mógłby przeżyć w krajach wysoko rozwiniętych („uprzemysłowionych”) z dochodu ocenianego jako całkowicie wystarczający do przeżycia w krajach biedniejszych („rozwijających się”), podobnie jak absurdem jest przeliczanie PKB PRL-u przy użyciu spekulacyjnego, czarnorynkowego kursu dolara USA względem złotówki.
Patrz: United Nations (ONZ) „Overall Socio-economic Perspective of the World Economy to the Year 2000” – „Ogólna perspektywa społeczno-gospodarcza gospodarki światowej do roku 2000” Nowy Jork: ONZ, 1990.
Herstoryk 23 CZERWCA 2022 7:53
Racja – jeśli owi paleo-konserwatyści w cokolwiek wierzą, to tylko w polityczny realizm, czyli w stosowanie siły, i to niekoniecznie „nagiej”.
Pozdrówka z Ger pod Warsze
LK
@PAK4
1. Rosja NIE napadła na Ukrainę, to Ukraina, a raczej jej władze, napadła na Rosjan zamieszkałych na Ukrainie. To dziadka Bidena i komika (rabina) Zieleńskiego, czy jak mu tam, należy postawić przed trybunałem za zbrodnie wojenne i przeciwko własnym narodom.
2. Nigdzie na tzw. Zachodzie nie ma demokracji czyli ludowładztwa, a jest tam tylko plutokracja, czyli władza najbogatszych kilku % ludności.
3. Dostarczanie broni, amunicji etc. Ukrainie przez Zachód jest zaś zbrodnią, gdyż niepotrzebnie przedłuża tę operację militarną Rosji, powodując niepotrzebną nikomu śmierć tysiecy mieszańców Ukrainy i ogromne zniszczenia jej infrastruktury.
4. To ty, a nie twoi adwersarze widzisz tylko biel („dobry” Zachód) i czerń („zły” Wschód”). Ja np. nie mam problemu z krytyką zamordyzmu w ChRL, ale rozumiem też, w odróżnieniu od ciebie, różnice kulturowe między np. Europą, czyli Azją Zachodnią, a Chinami, czyli Azją Wschodnią.
5. W zaborze rosyjskim tylko Wileńszczyzna była (i zresztą dalej jest, tyle że dziś w zaborze Litewskim) etnicznie polska. Warszawa, Poznań, Płock, Toruń, Bydgoszcz, Kalisz, Częstochowa czy Gdańsk były z zaborze Pruskim, a Kraków, Lwów, Przemyśl, Sandomierz czy Lublin w zaborze Austriackim.
Patrz np. https://pl.wikipedia.org/wiki/Rozbiory_Polski#/media/Plik:Rzeczpospolita_Rozbiory.svg .
6. Gender oznacza zaś, w pseudonaukowym żargonie tzw. genderowców, tzw. płeć kulturową, płeć społeczną, płeć kulturowo-społeczną, czasami także płeć psychologiczną lub psychiczną. Według Wikipedii jest to „zespół zachowań, norm i wartości przypisanych przez kulturę do każdej z płci”, „suma cech osobowości, stereotypów i ról płciowych (tak jakby cechy osobowe można było do siebie dodawać – LK), rozumianych w danym społeczeństwie jako kobiece lub męskie, przyjmowanych przez kobiety i mężczyzn w zakresie danej kultury w drodze socjalizacji, niewynikających bezpośrednio z biologicznych różnic w budowie ciała między płciami, czyli tzw. dymorfizmu płciowego”. Rodzaj nijaki w gramatce odnosi się zaś tylko do dzieci, a nie do dorosłych.
Shalom!
Link raz jeszcze:
Patrz np. https://pl.wikipedia.org/wiki/Rozbiory_Polski#/media/Plik:Rzeczpospolita_Rozbiory.svg .
Nie kopiuje się, a więc:
https://pl.wikipedia.org/wiki/Rozbiory_Polski
Calvin Hobbs 23 CZERWCA 2022 0:23
A było inaczej?
@PAK4
Michał Kleiber, w latach 2007–2015 prezes Polskiej Akademii Nauk, w wywiadzie radiowym uznał, że zamiana nauki w ideologię jest szkodliwa. Zachęcając do dalszych studiów nad płcią kulturową skrytykował pochopne przenoszenie powstających teorii na grunt społeczny. Krytycznie przez członków Komitetu Nauk Pedagogicznych PAN został oceniony poradnik dla nauczycieli przedszkolnych „Równościowe przedszkole. Jak uczynić wychowanie przedszkolne wrażliwym na płeć” napisany przez niejakie panie Annę Dzierzgowską, Joannę Piotrowską i Ewę Rutkowską z tzw. Towarzystwa Edukacji Antydyskryminacyjnej (poradnik ten jest w mediach określany jako „program”). W konkluzji opinii autorstwa dr hab. Józefy Bałachowicz na temat tego opracowania zostało ono określone jako „w wielu miejscach sprzeczne z założeniami edukacji dziecka”. W opinii tej stwierdzono też, że wbrew standardom edukacji seksualnej w Europie WHO „W przedstawionym programie zdecydowanie brak jest skierowania należytej uwagi na umacnianie własnej tożsamości płciowej dzieci”.
W Polsce sprzeciw większości rodziców wywołał projekt „Szczęśliwa 15”, realizowany w przedszkolach w Rybniku. Rodziców zaniepokoiły powtarzające się pytania dzieci powracających z przedszkoli, między innymi dotyczące ubierania się chłopców w sukienki. Większość rodziców zrezygnowała z udziału ich dzieci w projekcie, co spowodowało skreślenie ich dzieci z listy wychowanków przez dyrekcję przedszkola. Projekt ma według zwolenników na celu uczenie dzieci, że kobiety i mężczyźni mają równe prawa, ale przeciwnicy oskarżają ten projekt o propagowanie ideologii gender, która w oczywisty sposób podważa wartość, funkcje i prawa rodziny, stwarzając zagrożenie dla tożsamości człowieka.
Chrześcijanie i Starozakonni są zaś zdania, że gender jest ideologią o pseudomarksistowskich korzeniach, która promuje zasady całkowicie sprzeczne z rzeczywistością i zdrowym psychicznie pojmowaniem natury człowieka. Jej niebezpieczeństwo wynika także z głęboko destrukcyjnego charakteru zarówno wobec osoby, jak i relacji międzyludzkich, a więc całego życia społecznego. Więcej p. np. Wikipedia.
Szalom,
Twoje Cadyk z Ger i Warsze.
Jaki parasol ochronny dał zbiorowy chrzest 966 r. … Tak sobie myślę prywatnie … ochrzczeni póżniej obrywali od ojców chrzestnych najwięcej w okolicy …
Z „The New York Times” - Zełenski do Afryki: „To też wasza wojna”.
Prezydent Ukrainy, niejaki Wołodymyr Zełenski, lobbował w tym tygodniu w Unii Afrykańskiej o wsparcie. Stanął w obliczu trudnej bitwy, zwracając się do przywódców, którzy są blisko powiązani z prezydentem Rosji Władimirem Putinem. Wiele rządów afrykańskich unika potępienia Rosji, wstrzymało się od głosów ONZ potępiających tę operację i określiło ją jako nie mającą bezpośredniego wpływu na kontynent. Zełenski skupił się więc na ekonomicznych konsekwencjach tego konfliktu dla Afryki: wysokich cenach żywności spowodowanych wojną między dwoma największymi światowymi producentami zbóż, które pogorszyły brak bezpieczeństwa żywnościowego. „Afryka jest właściwie zakładnikiem” – powiedział Zełenski.
Tło: susza w Somalii i rosnący brak bezpieczeństwa żywnościowego w regionie Sahelu zwróciły uwagę na konsekwencje wzrostu cen żywności, zwłaszcza pszenicy. Rosną również koszty paliwa, co jeszcze bardziej ogranicza rodzącą się klasę średnią i miejską biedę na kontynencie.
Odpowiedź: Ogólnie rzecz biorąc, była stonowana. Moussa Faki Mahamat, przewodniczący Unii Afrykańskiej, ponownie wezwał do dialogu w celu zakończenia wojny. Prezydent Senegalu Macky Sall, występujący jako rotacyjny szef polityczny Unii Afrykańskiej, powiedział w tym miesiącu, że sankcje wobec Rosji powinny się skończyć, odnosząc się do Putina jako „drogiego przyjaciela Władimira”.
Więcej wiadomości z wojny na Ukrainie:
We wschodniej Ukrainie zbliża się decydująca rozgrywka, ponieważ Rosja zajmuje coraz więcej miast.
Finlandia i Szwecja, które ubiegały się o członkostwo w NATO po inwazji Rosji na Ukrainę, oczekiwały szybkiego przyjęcia do sojuszu. Turcja, numer dwa w NATO po USA, ma jednak inne zdanie na ten temat.
Nauka w minutę
Dziś w radiu Wrocław o osiągnięciach europejskiego teleskopu Gaia w badaniach Kosmosu.
Znacznie dłużej mówiono o zboczeńcach i degeneratach w politycznych ruchach europejskich.
Gościem był minister oświaty, a rozmowa dotyczyła historii i teraźniejszości.
Mam nadzieję, że te tematy jeszcze długo będą na tapecie
aka.cia 21 CZERWCA 2022 0:27
Spadaj prowokatorze z tego blogu! 🙁
ls42 23 CZERWCA 2022 8:53
Teleskop Geja?
markot 22 czerwca 2022 20:46
„Uprawa kukurydzy w Arizonie”
I w tym problem – pola o obszarze setek albo i tysięcy ha upraw monokulturowych, rok po roku to samo sprawiło, że podobno w USA 30% ziem uprawnych jest wyjałowione. Co roku „znikają” lasy tropikalne o powierzchni odpowiadającej powierzchni lasów w Polsce a nas uczono, że lasy tropikalne to płuca Ziemi.
Ktoś niedawno obliczył, że gdyby poziom konsumpcji na świecie był taki, jak w krajach zachodnich to już we wrześniu skończyło by się to, co natura jest wytworzyć w przeciągu CAŁEGO roku czyli byłaby zdolna pokryć ok. 75% potrzeb !
Ja pamiętam, jak ogłaszano w 1960-tym – liczba ludności świata przekroczyła 3 mld a minęło zaledwie 60 lat i już dobijamy do 8 mld. Gdyby nie restrykcyjna polityka demograficzna Chin byłoby nas już nawet 9 mld.
Jeśli w Europie w tym czasie liczba ludności wzrosła o 20-25% to są kraje – głównie w Azji i Afryce, gdzie liczba ludności wzrosła 4-5-krotnie.
Wiele by na ten temat można napisać lecz nie wiem, czy ten wątek „chwyci” bo to wg. mnie najistotniejszy problem – szczególnie w perspektywie naszych dzieci i wnuków.
PAK4 21 CZERWCA 2022 12:47
1. Pominąłeś dwa z użytych przeze mnie rankingów, a więc jesteś nieuczciwym dyskutantem. I skąd wiesz, kto studiuje w Moskwie? Byłeś tam może ostatnio? I czy to źle, że ktoś się uczy zagranicą, w tym u swych adwersarzy?
2. Znów piszesz bzdury na temat tego rzekomego wolnego rynku w handlu na wielką skalę. Poza tym, to w aeronautyce mamy regres, a nie postęp, i to od lat 1960-tych, czyli od czasu wyprodukowania pierwszych pasażerskich samolotów ponaddźwiękowych. W kosmosie też latamy bliżej niż pod koniec lat 1960-tych. Itp. Itd.
3. Samochody made in USA mają dziś jeszcze gorszą opinię.
4. Każdy korzysta z osiągnięć konkurencji i je naśladuje. A chińskie samoloty jakoś latają…
5. Brak odpowiedzi na pytanie, gdzie ty masz na świecie demokrację? Ty przecież mylisz jej pozory z rzeczywistym ludowładztwem, którego jednak nigdzie juz na świecie nie znajdziesz. I poza tym, to ja jestem socjalistą a nie ultrakonserwatystą. Walczysz więc z tzw. chochołem (własnej produkcji).
6. Powtarzam, że nam nie wolno jest dziś chronić tzw. infant industries, gdyż Niemcy czyli KE nam tego zabrania pod pozorem prowadzenia polityki wolnorynkowej, która nie pozwala na to, aby państwo finansowało owe infant industries, szczególnie zaś w domenie tzw. hig tech. Wpadliśmy więc w tzw. pułapkę średniego rozwoju i tylko opuszczenie UE umożliwi nam wyjście z tej pułapki.
7. Powtarzam – lobbowanie to jest po prostu przekupywanie i korumpowanie, tyle że w majestacie prawa.
8. Zachód wpadł w pułapkę stagnacji, genderyzmu, chowu wsobnego elit etc. Siłą Zachodu NIE była różnorodność i zdolność do adaptacji, wynikająca z nieistniejącej przecież demokracji, nieistniejącego wolnego rynku etc., a tylko brak moralnych skrupułów w podbijaniu i eksploatacji reszty świata. Chiny idą zaś inną drogą.
9. Chiny oczywiście mają swoje problemy, ale akurat problemu demograficznego to u nich nie ma, gdyż problemem Chin, tak jak prawie całego świata, jest dziś wciąż przeludnienie, a nie brak ludzi. Byłeś może kiedyś w Pekinie czy Szanghaju, że już nie wspomnę o Hong-Kongu? Poza tym, to AI robi tak szybkie postępy, że niedługo to trzeba bedzie mieć IQ (realne) dobrze w okolicach 140, aby znaleźć jakąkolwiek pracę. Lem się kłania…
Szalom!
kaesjot 23 CZERWCA 2022 8:58
To samo chciałem właśnie napisać, ale mnie uprzedziłeś.
P.S.
Jestem ZA wszystkimi liczbami, także i tymi nierzeczywistymi oraz nawet za NaN (Not a Number), czyli za wynikiem dzielenia przez zero. ;-)
Sahara … obszar pod palmy daktylowe, kokosowe, bananowe … tylko chcieć … Tak sobie myślę prywatnie … istniejące oazy pokazują realne możliwości … nawadnianie kropelkowe … do roboty … ! przekuwać miecze na lemiesze … !
kalvarya01 23 czerwca 2022 8:36
” Projekt ma według zwolenników na celu uczenie dzieci, że kobiety i mężczyźni mają równe prawa”
Tylko owi „zwolennicy” nie mogą zrozumieć, że NATURA wyznaczyła kobietom i mężczyznom INNE ZADANIA. Z tym wiążą się określone OBOWIĄZKI jak i szczególne PRAWA niezbędne do wypełnienia tych obowiązków.
SŁOWIANIN STANISŁAW 23 CZERWCA 2022 9:51
To NIE jest tak dobre geszeft jak wojna, mówi ci twoje cadyk z samego Ger.
kaesjot 23 CZERWCA 2022 9:54
Otóż to, ale wytłumacz to np. takiemu PAK4…
PAK4
23 CZERWCA 2022
7:45
Prostymi słowy ujmując, wszelkie interwencje wojskowe czy polityczne przeprowadzane przez zachód są słuszne.
Bez względu na ilość ofiar, bo to w imię demokracji?
Natomiast rosyjskie czy chińskie, należy potępić z założenia?
Pułkownik Baud polecany przeze mnie a nie czytany przez ciebie, obiektywnie przedstawił genezę konfliktu.
Kissinger niedawno przedstawił wnioski do realizacji w imię pragmatyzmu.
Na marginesie.
Amerykańsko- europejskie sankcje nakładane na Kubę, Koreę, Iran, Afganistan, Syrię czemu służa i w jakim celu są stosowane?
Zabijaja dziesiątki tysięcy ludzi rocznie.
Gdzie tu humanitaryzm, prawa człowieka, wolność handlu?
Bezwzględne podporzadkowanie własnym interesom swiata nie udało się dotąd nikomu.
Ale z uporem maniaka, Anglosasi wciąż próbują.
Bez względu na koszty ponoszone nawet przez własne społeczeństwa.
kalvarya01
Koncepcja prywatyzacji wszystkiego skutkuje maksymalizacją zysków nielicznych.
Zaniżając drastycznie dochód rozporządzalny społeczeństw które poszły tą drogą.
Efektem jest pauperyzacja mas, niespłacalne zadłużenie krajów.
Korzystają na tym jedynie czarodzieje kreujący z powietrza kredyty.
Schemat Ponziego własnie zaczyna się sypać.
I to dzięki głupocie decydentów
Niewielu ekonomistów, polityków, ogarnia reperkusje kolapsu systemu monetarnego.
Czas przygotować widły….
Głód w Afryce i krokodyle łzy Zełeńskiego … zamiast na zbrojenia banderowskiej Ukrainy zaopatrzenie Afryki w wodę … pompy zasilane solarnie … produkcja żywności nie zabija … Tak sobie myślę prywatnie … o ochronie życia poczętego aż do naturalnej śmierci …
Taka moja uwaga – gdyby Polską rządzili dziś Polacy, to wykorzystaliby obecną sytuację międzynarodową do finasowania ze skarbu państwa naszego własnego, czyli polskiego przemysłu wysokich technologii (hig tech), aby wydobyć Polskę z w/w pułapki średniego rozwoju, klasyfikując te wydatki jako militarne a więc objęte pełną i ścisłą tajemnicą państwową i wojskową, nawet wobec innych państw-członków UE i NATO, tak jak to robią w NATO np. USA.
wiesiek59 23 CZERWCA 2022 10:44
Otóż to…
wiesiek59 23 CZERWCA 2022 10:37
Pełna zgoda, ale czy to trafi do @PAK4?
https://weltwoche.ch/daily/this-war-has-been-lost-a-long-time-ago/
=========
Jeden z nielicznych trzeźwych zachodnich analityków.
@SŁOWIANIN STANISŁAW – 10:47
„Głód w Afryce i krokodyle łzy Zełeńskiego … zamiast na zbrojenia banderowskiej Ukrainy..”
Tu masz coś w zbliżonym tOmacie
„Przyszła premier Kanady musi się przyznać do dziadka-kolaboranta nazistowskiego. Baza wyborcza wicepremier Chrystii Freeland znajduje się w kanadyjskiej diasporze ukraińskiej, która przemianowała nazistowskich kolaborantów na nacjonalistycznych bohaterów wojennych.”
https://www.tabletmag.com/sections/news/articles/chrystia-freeland-needs-to-come-clean-about-her-nazi-collaborationist-grandfather
Z doniesień „Ottawa Citizen” wynika, że kanadyjscy wojskowi spotkali się z liderami Azowa w czerwcu 2018 r. i zamiast zdystansować się od jednostki, wyrazili jedynie obawę, że informacja o niej może wyciec do mediów. W odpowiedzi na pytania Citizen, rzecznik Kanadyjskich Sił Zbrojnych Lt.-Cmdr. Julie McDonald powiedziała, że to Ukraina jest odpowiedzialna za sprawdzenie własnych sił pod kątem skrajnie prawicowego ekstremizmu.
Azow, oczywiście, nie jest reprezentatywny dla Ukrainy, której żydowski prezydent odniósł w 2019 r. spektakularne zwycięstwo wyborcze. W tym samym roku koalicja skrajnie prawicowych partii powiązanych z Azowem otrzymała zaledwie 2% głosów, czyli znacznie poniżej progu wymaganego do zasiadania w parlamencie. Jednak po inwazji Rosji Azow został włączony do ukraińskiej Gwardii Narodowej, aby pomagać w walce z rosyjskimi separatystami na wschodzie Ukrainy.
Wojna stwarza nieciekawych sojuszników i wielu powiedziałoby, że trzymanie nosa na pulsie, gdy częściowo polegamy na grupach takich jak Azow, aby zapewnić pewien opór wobec rosyjskiej agresji, jest najmniej złą opcją dostępną dla proukraińskiej, antyrosyjskiej polityki. Jednak w kraju takim jak Kanada, gdzie historyczne tłumienie nazistowskiego kolaboracjonizmu jest nie tylko tolerowane, ale wręcz forsowane na najwyższych szczeblach władzy, wyborcy mają pełne prawo zastanawiać się nad osobą, która według wielu będzie naszym następnym premierem.
(Przetłumaczono z http://www.DeepL.com/Translator (wersja darmowa) )
https://www.moonofalabama.org/2022/06/the-neocons-dream-decolonize-russia-re-colonize-china-.html#more
===========
O mokrych snach neokonów….
Banderowska diaspora ma się dobrze po ucieczce z katolickim wehrmachtem z pomocą Watykanu … warto pytać o przodków obrońców z Kanady i jankesów … o Israelu nie wspomnę … Tak sobie myślę prywatnie …Żyd na czele banderowskiej Ukrainy dodaje splendoru całej sprawie … haj … !
Ursula von der Leyen musi być jednym z najbardziej niekompetentnych idiotów w UE, a konkurencja jest niezwykle ostra. Jej najnowsza prognoza: Komisja Europejska „docenia ogromny postęp, jaki osiągnęła demokracja od czasu protestów na Majdanie w 2014 roku”. Skatalogujmy niektóre z tych „postępów”, w dowolnej kolejności:
* zakaz działalności wszystkich opozycyjnych partii politycznych i ścigania przeciwników politycznych
* zakaz wszelkich mediów opozycyjnych i nacjonalizacja pozostałych mediów
* zakaz książek, muzyki i edukacji w podstawowym języku używanym przez większość ludności (od wieków) lub produkowanym przez etniczni Rosjanie (którzy również stanowią około połowy populacji)
* wydalenie Rosyjskiego Kościoła Prawosławnego, do którego należała większość Ukraińców
* gloryfikowanie antydemokratycznych ultranacjonalistów
* odmowa honorowania jedynych plebiscytów/referendów, jakie kiedykolwiek odbyły się na Ukrainie
* przymusowy pobór do służby wojskowej i przymusowe przeniesienie na front, bez broni, szkolenia i dowództwa, milionów ludzi”
* żałosną odmowę honorowania zobowiązań podjętych podczas kampanii prezydenckich i ustawodawczych
* masową i wszechobecną korupcję, w tym (a) urzędnicy sprzedający żywność i wojskową „pomoc” w celu wzbogacenia się; i (b) odmowa zgłaszania ofiar wojskowych, aby nie trzeba było wypłacać zasiłków z tytułu śmierci rodzinie zmarłego, a wypłata wynagrodzenia zmarłego (choć skromna, jest ich dużo) może zostać zabrana przez skorumpowanych urzędników
* szeroko rozmieszczanie szwadronów śmierci i terroru, w tym porwania, tortury i mordowanie dziennikarzy i obywateli
* przejmowanie mienia i odebranie obywatelstwa osobom przeciwnym partii rządzącej
* odmowa pomocy i innych korzyści milionom obywateli w oparciu o ich położenie na obszarach, które sprzeciwiały się puczowi i nowym władcom
* całkowita dominacja polityki przez obce mocarstwa
* itd., itd., itd.
Trudno znaleźć mniej demokratyczny kraj na świecie, być może Arabię Saudyjską i Koreę Północną, ale nawet one nie są dane.
Nie bez ironii, że sama KE jest instytucją antydemokratyczną, oligarchiczną.
Wysłane przez: CalDre | 22 czerwca 2022 19:39 | 43
Jedyna dekolonizacja stref jest pilnie potrzebna na zbiorowym Zachodzie. Zastanawiam się, kto wyzwoliłby zakłopotaną ludność Zachodu z uścisku ich władców Draculi.
Wysłane przez: Steve | 22 czerwca 2022 19:41 utc | 44
==========
Celne podsumowanie…..
wiesiek59 godz. 11.46
Coś musiało być na rzeczy skoro Rosjanie upomnieli się o swoje.
Bardzo celny ten komentarz.
W tygodniku POLITYKA artykuł „Miasto umarłych”
Dobry tekst i zdjęcia.
https://www.csce.gov/international-impact/press-and-media/press-releases/decolonization-russia-be-discussed-upcoming
DEKOLONIZACJA ROSJI DO OMÓWIENIA NA NADCHODZĄCYM SPOTKANIU KOMISJI HELSIŃSKIEJ
1. To jest autentyczne, jest to domena .gov. Zastanawiam się, kiedy to usuną i twierdzą, że to rosyjska dezinformacja.
2. „Jego agresja katalizuje także od dawna spóźnioną rozmowę na temat wewnętrznego imperium Rosji, biorąc pod uwagę dominację Moskwy nad wieloma rdzennymi narodami nierosyjskimi”
Chodzi o rozbicie Rosji na mniejsze kawałki. Czy istnieje inny sposób interpretacji tego bezpośredniego cytatu?
3. Lista rosyjskich „wojn barbarzyńskich”, Ukraina, Syria, Czeczenia, Gruzja…
Ukraina – prawdopodobnie agresja, ale 100% BS donosi o zachowaniu.
Syria – totalne kłamstwa, Czeczenia – to był brutalny konflikt, Gruzja – brutalna? To był bardzo ograniczony konflikt militarny.
Wysłane przez: Christian J. | 22 czerwca 2022 20:21 |
========
Zdaje się ktoś myśli że ma w ręku jakieś silne karty….
Poziom głupoty polityków zachodnich jest przerażający.
W jakim świecie oni żyją?
Narkotycznych wizji?
Czy majdan różni się od szturmu podżeganego przez Trumpa … Tak sobie myślę prywatnie … jakie „demokracje” takie metody … na tym tle Okrągły Stół Jaruzelskiego bardziej cywilizowany …
W ostatnich tygodniach tak zwanej dyplomacji Zachód samozwańczo trzymał się swojego poglądu, że Rosja jest wrogiem i nie ma racji, a siebie przedstawiał jako tego dobrego i prawego. W odpowiedzi na zmasowane działania wojsk rosyjskich, Zachód nieustannie zapowiadał wprowadzenie własnej armii poważnych konsekwencji ekonomicznych, mających na celu sparaliżowanie rosyjskiej gospodarki. Tak więc impas trwał, dopóki Rosja nie zrobiła tego, czego chciała.
Być może było to nieuniknione, bo być może Władimir Putin był zdeterminowany, by odzyskać Ukrainę, ale gdyby Zachód spróbował spojrzeć na sytuację przez pryzmat Rosji, to nawet gdyby Putin był nastawiony na inwazję, byłoby to o wiele trudniejsze do przeprowadzenia, ponieważ ukradłby narrację, którą wykorzystał dla rosyjskiej konsumpcji.
Zachód, a zwłaszcza Ameryka, kurczowo trzyma się przekonania, że mamy rację, że jesteśmy dobrymi ludźmi na świecie i że to, jak według nas powinny działać państwa, jest właściwą drogą. Upieramy się, że nasza wersja demokracji i wolności jest właściwa, a potem pouczamy innych przywódców, jak mają zarządzać swoimi krajami. To szczególnie denerwuje Chiny, które ze swoimi sukcesami gospodarczymi i społecznymi w zarządzaniu narodem liczącym 1,4 miliarda ludzi oraz bogatą, tysiącletnią historią słusznie uważają to za brak szacunku i protekcjonalność. Rosja, znając historię, podobnie dostrzega poczucie uprawnienia leżące u podstaw zachowania Zachodu.
Putin uważał rozszerzenie NATO na Ukrainę, dawną integralną część kraju, z którego się urodził – ZSRR, za pozwolenie na to, by sojusz otwarcie wrogi Rosji znalazł się u jej granic. Oczywiście, musiał wyznaczyć granicę. Ameryka zrobiła dokładnie to samo z Kubą w 1961 roku i z Irakiem w 2003 roku. Aby Zachód uznał to za uzasadnione, a jednocześnie odrzucił podobne obawy Rosji, musiał oczywiście nastąpić odwet ze strony Rosji.
Putin wielokrotnie twierdził, że Zachód nie słucha obaw Rosji, i faktycznie tak nie było. Zachód upierał się, że Ukraina ma prawo do dowolnego związku z NATO, mimo że jest to całkowicie sprzeczne z tym, co Ameryka, a prawdopodobnie także każdy inny naród na Zachodzie, zaakceptowałby, gdyby role się odwróciły. Ta arogancja i fałszywe przekonanie o własnej potędze sprawiły, że konfliktu nie dało się rozwiązać.
Dla świętego spokoju zaprosić Rosję do Unii i NATO … Tak sobie myślę prywatnie … wtedy dla podżegaczy wojennych życie straci sens …
SŁOWIANIN STANISŁAW
23 CZERWCA 2022
12:27
Bez wroga, kompleks militarno- przemysłowy straciłby rację bytu.
Dlatego życie w pokoju na tej planecie jest niemozliwe.
ZYSK jest WSZYSTKIM, zycie ludzkie NICZYM.
Szczególnie gdy chodzi o życie „kolorowych” i plebsu zaciągającego się do armii.
Czy dla religii ZYSK jest WSZYSTKIM, życie ludzkie NICZYM … Tak sobie myślę prywatnie … czyja władza taka religia …
Zaciekle oślepiające światło blogowych kwazarów nie odróżniających we własnym świetle ( oślepia jak leci ) kawalerii od Kalwarii – cudzej korupcji od własnej ..
Każda bliska nam ( po sąsiedzku )korupcja była , jest i będzie nasza – musi byc’ .
Zostanie pożarta jak slowo „napisane ” i przeczytane przez nas
Tnp w odwrotnej kolejności bo nie wyrzygane w towarzystwie blogowym .
Tego sie tu i tam nie robi
…………….
„Coś musiało być na rzeczy skoro Rosjanie upomnieli się o swoje. ”
……………
„* przymusowy pobór do służby wojskowej i przymusowe przeniesienie na front, bez broni, szkolenia i dowództwa, milionów ludzi”
* żałosną odmowę honorowania zobowiązań podjętych podczas kampanii prezydenckich i ustawodawczych
* masową i wszechobecną korupcję, ”
read://https_phys.org/?url=https%3A%2F%2Fphys.org%2Fnews%2F2020-10-simulations-webb-telescope-reveal-distant.html
„Kwazary są najjaśniejszymi obiektami we wszechświecie i jednymi z najbardziej energetycznych. Przyćmiewają całe galaktyki miliardów gwiazd. Supermasywna czarna leży w sercu każdego kwazara, ale nie każda czarna jest kwazarem. Tylko czarne, które żywią się najbardziej żarłocznie, mogą zasilać kwazar. Materia wpadająca do supermasywnej czarnej nagrzewa się i powoduje, że kwazar zaciekle świeci we wszechświecie jak latarnia morska. „
Czy religie są na smyczy polityków … Tak sobie myślę prywatnie … co było wprzódy polityka czy religia … kto jest ogonem … do merdania …
SŁOWIANIN STANISŁAW
23 CZERWCA 2022, 12:41
Czy dla ateizmu (ateizacji) ZYSK jest WSZYSTKIM, życie ludzkie NICZYM? Tak sobie pytam daremnie… Czyja władza, taka ideologia/religia, wiara/niewiara (wsio rawno)…
Niczego nie było najpierw – jeśli chodzi o to, o czym rzecz – polityka, religia, wiara, niewiara, ateizm – wszystko to z jednego wora i tylko kolor worka każdy maluje na swoja barwę, ale wór to wór …
Kto merda? Każdy, tylko zależy komu i z jakiego powodu.
Świat częściej o Putinie niż o bogu … Tak sobie myślę prywatnie … z tego się żyje …
@Pak4 – Twój Idol, czyli Dziadzio Biden nie wie co robić:
Ceny paliw rekordowe w USA. Joe Biden chce wprowadzić wakacje podatkowe. Ekonomistów to nie zachwyca Eryk Kielak Wyborcza 23.06.2022 11:26
Prezydent USA Joe Biden wezwał 22 czerwca Kongres do zawieszenia podatków od paliwa w Stanach Zjednoczonych. Ceny miałyby dzięki temu spaść o kilka centów. Rozwiązanie obowiązywałoby przez trzy miesiące. – Same wakacje od podatku nie rozwiążą problemu, ale zapewni to rodzinom natychmiastową ulgę – tłumaczy swój pomysł prezydent Biden, Cena jednego galonu (3,7 litra) benzyny w USA to 5 dolarów. Rok temu były to 3 dolary. W opłatę tą wliczone są podatki – 18 centów za galon na benzynie i 24 ceny za olej napędowy. Poszczególne stany mogą go modyfikować. W Pensylwanii podatek ten jest np. ponad trzykrotnie wyższy, a z drugiej strony Nowy Jork już zawiesił te opłaty. Jeżeli pomysł wakacji podatkowych Joe Bidena wszedłby w życie, w budżecie pojawiłaby się dziura na 10 mld dolarów, które pochodzą właśnie z tego podatku.
Duże koszty takiego rozwiązania to nie jedyny problem Bidena. Nie wszyscy politycy i ekonomiści popierają ten pomysł. BBC podaje, że w Kongresie nie ma przekonania co do wakacji podatkowych. Jeden z republikańskich senatorów odrzucił w środę tę propozycję, nazywając ją „sztuczką”. Nawet członkowie partii Bidena wyrażają obawy, że posunięcie to przyniosłoby korzyści przede wszystkim firmom naftowym i gazowym.
Komentarz (nie mój):
Lunatykowi z Białego Domu otworzyły się na moment śpiące ślipia i zobaczył do jakiego syfu doprowadził Amerykę w przeciągu półtora roku swoich nieudolnych rządów i absurdalnych decyzji przez uległości wobec doktryny skrajnie lewackiemu nurtowi w swojej partii.
Teraz ten demagog chce zrobić z siebie dobroczyńcę i przy wyciskaniu od Amerykanów dodatkowych setek dolarów każdego miesiąca, zamierza podarować kilkanaście dolarów w skali trzech miesięcy, żeby zwiększyć szanse skompromitowanych Demokratów na wygranie w midterm elections ;-). To tylko kolejny przyklad jak ten stetryczały demagog oderwany jest od rzeczywistości.
Orteq 23 CZERWCA 2022 12:01
Pełna zgoda, ale czy to trafi do @PAK4?
wiesiek59 23 CZERWCA 2022 11:56
Oni żyją razem z @PAK4 w tzw. fool’s paradise czyli raju głupców i to na nasz koszt.
:-(
Paliwa od jankesów to krwawica rdzennej ludności przed pacyfikacją w rezerwatach … Tak sobie myślę prywatnie … tankujesz paliwo jankesowego pochodzenia daj datek na wywłaszczonych mieszkańców rezerwatów i Guantanamo …
ontario 23 CZERWCA 2022 13:09
Dlaczego dla kościoła ZYSK jest WSZYSTKIM a życie ludzkie, szczególnie zaś kobiety w ciąży -NICZYM?
https://wiadomosci.gazeta.pl/wiadomosci/7,114881,28613548,malta-odmowila-aborcji-amerykance-zycie-kobiety-moze-byc-zagrozone.html#s=BoxOpImg3
Masę słów, a sensu brak, więc co ma do mnie trafić? Może Panowie ustalą jakąś choćby jedną tezę, która byłaby jako tako przekonująca? „Fakty” trzymają się luźnie rzeczywistości a logiki brak. I ja teraz nie wiem, czy rechotać nad tymi „obawami Rosji” (że co, że jak puścić im „Szczęki”, to zbombardują każdego kto nie wybija rekinów?), czy płakać, bo w Ukrainie na serio giną ludzie.
@Wiesiek59:
> Prostymi słowy ujmując, wszelkie interwencje wojskowe czy polityczne przeprowadzane przez zachód są słuszne.
Bez względu na ilość ofiar, bo to w imię demokracji?
Pudło.
@kalvarya01:
> Każdy korzysta z osiągnięć konkurencji i je naśladuje. A chińskie samoloty jakoś latają…
Żadnego samolotu pasażerskiego nie wprowadzili do użytku, bo jeszcze nie uzyskali certyfikacji 😛
> Powtarzam, że nam nie wolno jest dziś chronić tzw. infant industries
Powtarzam, że kłamiesz Pan.
> Powtarzam – lobbowanie to jest po prostu przekupywanie i korumpowanie, tyle że w majestacie prawa.
Powtarzam, że kłamiesz Pan.
> NIE była różnorodność i zdolność do adaptacji, wynikająca z nieistniejącej przecież demokracji, nieistniejącego wolnego rynku etc., a tylko brak moralnych skrupułów w podbijaniu i eksploatacji reszty świata. Chiny idą zaś inną drogą.
To dlaczego światem nie rządzi Rosja?
P.S.
Izrael ma teraz poważny problem, gdyż Indonezja – najludniejsze islamskie państwo świata (muzułmanami jest tam prawie 90%% populacji, czyli ponad 210 mln osób) i z PKB siódmym na świecie a więc większym niż PKB takich państw jak np. UK, Brazylia, Francja, Turcja, Meksyk, Korea Płd., Italia, Kanada, Australia etc. jest zdecydowanie antysyjonistyczne, a tamtejsi przewódcy nie dają się ogłupiać jankesom tak jak Arabowie.
MIT O „Masakrze na Placu Tiananmen” jest prawdopodobnie najbardziej udaną kampanią dezinformacyjną współczesnych czasów, według źródeł zachodnich i wschodnich – do tego stopnia, że dumni specjaliści od wojny psychologicznej wykorzystali ją niedawno do REKLAMOWANIA swoich umiejętności manipulowania wiadomościami. Dojdziemy do tego poniżej.
https://www.fridayeveryday.com/how-psy-ops-warriors-fooled-me-about-tiananmen-square-a-warning/
=========
PAK4 23 CZERWCA 2022 13:32
1. To u ciebie zauważam masę słów, a sensu brak i że nic do cie nie trafia, co nie jest zgodne z linią reżimowej, zachodniej propagandy.
2. Tak, na Ukrainie na serio giną ludzie, aby utrzymać megomie USA na tzw. Zachodzie. Twym zdaniem, to .
wszelkie interwencje wojskowe czy polityczne przeprowadzane przez zachód są słuszne, bez względu na ilość ofiar, bo to w imię tzw. demokracji. Nic ci nie mowi lista interwencji USA??
3. Comac C919 – dwusilnikowy samolot pasażerski, odrzutowiec wąskokadłubowy, zaprojektowany i produkowany przez Comac w Chińskiej Republice Ludowej. Pierwszy raz zaprezentowany został pod koniec 2015 roku.
4. Jakie masz dowody, że kłamię? Po prostu Niemcy i Francja blokują każdą próbę Polski, aby finansować swój własny przemysł, własną naukę etc., gdyż nie chcą, aby Polska stalla się konkurencyjna wobec Niemiec i Francji także w tzw. high tech, czyli nowoczesnych technologiach.
5. Lobbowanie to jest po prostu przekupywanie i korumpowanie, tyle że w majestacie prawa. Zresztą cały Zachód opiera się na korupcji, złodziejstwie, oszustwach etc. Działalność lobbingowa i w Polsce, i na świecie nie została sensownie uregulowana. Instytucje zaś, które powinny ją ucywilizować, żeby przestała kojarzyć się z korupcją, zajmują się sprawami formalnymi czwartego rzędu.
Z badań dowiadujemy się, że 12 procent polskich parlamentarzystów zdecydowanie negatywnie ocenia lobbing. Wszelkie inne opinie o ustawie o lobbingu funkcjonującej w polskim systemie od ponad trzech lat także przeważnie są krytyczne. Problemy senatora Misiaka i innych czołowych polityków pokazują jednocześnie, że problem lobbingu ciągle pozostaje nierozwiązany.
W USA działalność lobbingowa tysięcy grup interesu jest na stałe wpisana w życie polityczne i gospodarcze. Jest również stale krytykowana jako usankcjonowana prawem korupcja.
https://prawo.gazetaprawna.pl/artykuly/323599,czy-lobbing-to-korupcja-czy-raczej-wywieranie-dozwolonego-wplywu-na-stanowienie-prawa.html
6. Niebawem światem będą rządzić Chiny, India i Rosja.
GDP (PPP, US$ million) by country or territory:
Kraj region IMF(MFW) Rok Bank Światowy Rok CIA Rok
China Asia 30,177,926 2022 24,273,360 2020 23,009,780 2020
United States Americas 25,346,805 2022 20,936,600 2020 19,846,720 2020
European Union Europe 23,730,275 2022 20,046,175 2020 19,885,625 2019
India Asia 11,745,260 2022 9,907,028 2020 8,443,360 2020
ASEAN Asia 10,131,237 2022 8,238,168 2020 7,826,781 2020
Japan Asia 6,110,075 2022 5,328,033 2019 5,224,850 2019
Germany Europe 5,269,963 2022 4,469,546 2020 4,238,800 2020
EAEU Eurasia 5,242,218 2022 4,896,309 2020 4,606,458 2019
Russia Europe 4,365,443 2022 4,133,084 2020 3,875,690 2020
Indonesia Asia 3,995,064 2022 3,302,377 2020 3,130,470 2020
United Kingdom Europe 3,751,845 2022 3,019,057 2020 2,797,980 2020
Brazil Americas 3,680,942 2022 3,153,597 2020 2,989,430 2020
PAK4 23 CZERWCA 2022 13:32
The Eurasian Economic Union (EAEU or EEU) czyli Euroazjatycka Unia Gospodarcza, EUG (ros. Евразийский экономический союз, biał. Еўразійскі эканамічны саюз, kaz. Еуразиялық экономикалық одақ, orm. Եվրասիական տնտեսական միություն, kir. Евразиялык экономикалык биримдик, ang. Eurasian Economic Union, EAEU) jest to unia gospodarcza powołana 29 maja 2014 przez trzy państwa założycielskie: Białoruś, Republikę Kazachstanu i Federację Rosyjską. Do unii dołączyły także Armenia (10 października 2014 roku) oraz Kirgistan (23 grudnia 2014 roku). Traktat powołujący do życia Unię przewiduje poszerzenie dotychczasowej unii celnej o swobodny przepływ kapitału, siły roboczej, towarów i usług. Unia ta jest w publicystyce często określana jako alternatywa dla Unii Europejskiej.
SS
23 CZERWCA 2022
10:47
„Głód w Afryce i krokodyle łzy Zełeńskiego … zamiast na zbrojenia banderowskiej Ukrainy zaopatrzenie Afryki w wodę … ”
Widzę, że Polityka chętnie daje wszelkim faszystom, sowieckim bydlakom, niewydarzonym esbekom oraz innym ofiarom Stomilu wolną trybunę do siania bzdur, nienawiści oraz ruskiej propagandy.
Czy doprawdy parciane, cerowane gacie Matuszki są aż tak atrakcyjne dla szerokiego grona czytelników? Czy kalwaryjskie wodogłowie musi być tu eksponowane 24/7 ?
aka.cia 23 CZERWCA 2022 14:37
Spadaj jankeski pachołku z tego blogu. Za wysokie tu progi na twe chamskie nogi!
@wiesiek59:
:LOL:
Wiesz, że szerzysz jako prawdę, tekściki firemki z ograniczoną odpowiedzialnością kierowaną przez wysoką szychę w kontrolowanych przez ChPK władzach?
Swoją drogą, finanse Polityki, czy Guardiana, którym w miarę ufam, są przejrzyste. To nie są media zależne od sponsorów*, a tym bardziej central wywiadowczych. W ogóle, poprosiłbym o wskazanie medium zależnego od jakiegoś wywiadu. Bo tak sobie rzucacie oskarżeniami bez pokrycia…
*) Tu uwaga: w „zachodnim świecie” istniał ideał rozdzielności księgowości i managementu firm medialnych, oraz redakcji. Wiem, że nie zawsze idealnie realizowany, ale jednak — w ogóle to całe pisanie, że ktoś pisze za pieniądze i na zlecenie wywiadów podpada pod bardzo wredną insynuację. I to niczym nie popartą. Ale wiem, rozumiem, jak się wpadnie w wir teorii spiskowej to trzeba sobie jakoś radzić z odrzuceniem obiektywnej rzeczywistości.
@kalvarya:
> Tak, na Ukrainie na serio giną ludzie, aby utrzymać megomie USA
Przypominam, że to Rosja zaatakowała, przepraszam — poprowadziła specjalną operację militarną — bez cienia usprawiedliwienia dla swoich działań.
To co tu piszecie nie trzyma się kupy. Nic z tego co piszecie, nie wiąże się logicznie z usprawiedliwieniem inwazji. (Zostawiam na boku, że duża część to kłamstwa. Kłamać jest łatwo, a prostowanie to ciężka praca. Możesz triumfować, bo ja już na sprawdzanie, weryfikowanie i prostowanie nie mam sił. Zwłaszcza, jak kłamiący nie chcą słuchać.)
> Comac C919
Tak. O nim pisałem. Nie przeszedł certyfikacji.
Nie wyrzucam tego Chińczykom — są nowi, to się czasem przedłuża, ale moje nie-wyrzuty nie zmieniają faktu, że nie znalazł się jeszcze w eksploatacji, a Ty mówisz, że latają.
W części blogów, gdzie się kręciłem, mówiono pogardliwie research ziemkiewiczowiski na tak jest, bo mi się tak wydaje. Mam to zmienić na research kalvaryjski?
> Jakie masz dowody, że kłamię?
Pisałem: miewam osobisty kontakt z procesem przyznawania środków na rozwój technologiczny polskich firm z pieniędzy unijnych. To się dzieje w realnym świecie.
> Lobbowanie to jest po prostu przekupywanie i korumpowanie
Szanowny Pan nadal nie przeczytał co to jest „lobbing”, tylko rzuca słowami wylosowanymi kostką do gry?
> Niebawem światem będą rządzić Chiny, India i Rosja.
Triumfalizm chiński rozumiem — proste przedłużenie trendów może im dać „rządzenie światem” za kilkadziesiąt lat. Ale Indiom już tak dobrze nie idzie. A Rosja się stacza.
kalvarya,
Wykwintnego języka oraz bogactwa wodogłowych myśli, nikt Lesiowi nie odbierze. Z kolei komenda „spadaj” nie działa już tak piorunująco skutecznie jak w złotych dla esbeków czasach. Możesz to teraz wykrzykiwać między szpalerami łóżek w domu starców, ale na blogu prowokuje jedynie do ziewania.
Sorry Lesiu, cuśniecuś w twym żywocie się umoczyło – postawiłeś na kulawego konia, stąd chyba ta deprecha oraz myślowa sraczka. Potrzebujesz więcej miłości, być może wiernego partnera, który codziennie będzie powtarzał: Lechu, ty to jesteś qwa geniusz!
PAK4
23 CZERWCA 2022
15:20
Posługiwanie się zdrowym rozsądkiem, śledzenie przepływów pieniędzy, określenie kto na tym korzysta, jest bardzo prostym systemem orientacji w świecie.
Nie zawadzi też posługiwanie się logiką i znajomoscią motywów ludzkich postępowań w znanych sytuacjach.
Większość zachowań jest przewidywalna i INTENCJONALNA.
Wierzysz w bezstronność mediów skupionych w 6 korporacjach zachodnich?
Ja nie, bo od dziesięcioleci łżą jak bure suki, kreując rzeczywistość nieprzystającą do faktów.
Dysonans poznawczy jest zbyt silny by uwierzyć w fikcję.
Z biegiem lat, zdobyłem kolekcję kilkunastu autorów, ponad 100 portali.
Ich teksty spełniają kryteria rzetelności, dają doskonały z mojego punktu widzenia obraz swiata.
Diametralnie różny od twojego.
Iest to spektrum globalne, nie lokalne.
Moim zdaniem, krawędź klifu jest już bardzo blisko.
Lemingi NAPRZÓD!!!
Jeden z sensowniejszych amerykańskich prezydentów ujął problem lakoniczni:
EKONOMIA GŁUPCZE.
I tu rozstrzygnie się zwycięstwo w wojnie Wschodu z Zachodem.
Niedostosowani zginą.
Era jednobiegunowego świata dobiegła końca.
Zerwanie z Zachodem jest nieodwracalne i ostateczne. Żadna presja z Zachodu tego nie zmieni.
Rosja odnowiła swoją suwerenność. Wzmocnienie suwerenności politycznej i gospodarczej jest absolutnym priorytetem.
UE całkowicie utraciła suwerenność polityczną. Obecny kryzys pokazuje, że UE nie jest gotowa do odgrywania roli niezależnego, suwerennego aktora. To po prostu zespół amerykańskich wasali pozbawionych jakiejkolwiek suwerenności polityczno-wojskowej.
Suwerenność nie może być częściowa. Albo jesteś suwerenem, albo kolonią.
https://www.unz.com/pescobar/exile-on-main-street-the-sound-of-the-unipolar-world-fading-away/
===========
I wszystko na ten temat…
Zachodnim mediom udało się skolonizować umysły mieszkańców.
Niewielu dostrzega że KRÓL JEST NAGI.
@wieśku59:
> Posługiwanie się zdrowym rozsądkiem
Wieśku, nie obraź się, ale ja właśnie tego zdrowego rozsądku nie widzę. Symbolem jest tu kalvarya, który wrzuca jakieś dane, jak mu się wskaże, że nie pasują do jego tezy, to zaczyna walczyć z własnymi źródłami. Ale to co przytaczasz też się często kupy i logiki nie trzyma.
Zresztą, jakie pieniądze śledzisz? Sięgnąłeś po dane giełdowe Polityki? Sprawdziłeś finanse Guardiana? Idę o zakład, że nie wiesz, za co oni piszą i publikują…
> Większość zachowań jest przewidywalna i INTENCJONALNA.
O, mamy temat naukowy 🙂
No nie wiem. Ktoś to liczył? Gdy stukam w klawiaturę nie mam wielkich intencji, a już na pewno zachowanie moich palców jest zautomatyzowane — nawet nie patrzę na klawiaturę, słowa same zamieniają się w literki. Czasem z pominięciem ortografii i gramatyki…
Serio, to ludzie mają bardzo dużo zachowań nieintencjonalnych, odruchowych, wyuczonych itp.
> Wierzysz w bezstronność mediów skupionych w 6 korporacjach zachodnich?
Guardian?
Polityka?
Ziemowit Szczerek?
Tak pierwsi z brzegu moi ulubieńcy.
Serio — ja się tu nie mogę odnieść, bo nie wiem, jakie korporacje masz na myśli, poza tym, że zachodnie, czyli Xinhua wykluczasz, na przykład. Ale co do reguły — tak — powiązanie między sponsorem a wymogiem pisania pod jego dyktando jest większe w Chinach, czy Rosji, niż w Stanach. Jest większe w blogu, którego powiązania ze sponsorami na Kremlu czy w Pekinie da się wyśledzić w pół godziny. Albo w skrajnie prawicowej organizacji założonej za pieniądze zagranicznych, zideologizowanych sponsorów. Że tak podsumuję trzy z Twoich ulubionych źródeł.
> kreując rzeczywistość nieprzystającą do faktów.
Ekhm… Przy okazji „Polski w ruinie”, znanego hasła, znanej partii, to moja żona sobie kpiła, że wystarczy zerknąć za okno by sprawdzić jaka jest prawda.
Ja wiem, nie pojedziemy na front w Ukrainie by sprawdzić, ale wiele rzeczy widać, wystarczy „wyjrzeć za okno”.
> Ich teksty spełniają kryteria rzetelności, dają doskonały z mojego punktu widzenia obraz swiata.
Paru z nich tu zweryfikowałem — jak widzisz, negatywnie. Setki nie dam rady — i tak sobie wyrzucam, że marnuję tu z Wami strasznie dużo czasu.
> Lemingi NAPRZÓD!!!
OK, zaraz się zbieram na rower i pojadę naprzód, a nawet na zachód 😀
Pozdrowienia!
kalvarya01
23 czerwca 2022
8:27
Trzeba było tam być żeby wiedzieć kto na kogo napadł.
@wiesiek59 &PS:
Natlenienie rowerowe przypomniało mi, że nie napisałem jednej ważnej rzeczy. Otóż te Twoje źródła, które widziałem, to nie były źródła informacji, a źródła opinii. To istotna różnica.
W przypadku źródeł informacji, redakcja może wysłać dziennikarza na miejsce, oraz powinna mieć kogoś, kto sprawdzi jego informacje. Dużym, poważnym redakcjom zdarzają się wpadki, ale pojedyncze, a nie seryjne. Przykłady z czasów kampanii Trumpa wskazywały, że jedna pojedyncza duża redakcja, poważnego medium potrafiła się nabrać na fake newsa, ale nie było przypadku, by taki fake news obleciał więcej redakcji, wydań gazet, telewizji itp. Kolejne redakcje weryfikowały i zatrzymywały rozprzestrzenianie się fake newsa, nawet gdy uderzał on w człowieka przez nich nielubianego.
Inaczej było z portalami blogowymi i, oczywiście, Fox News. One nie weryfikowały wygodnych informacji, tylko przesyłały je dalej, pozwalając im „rezonować”.
Tak, tu możemy sobie razem (?) ponarzekać na obecny kapitalizm, który szuka redukcji kosztów. Porządna redakcja, zatrudniająca ludzi do weryfikacji, czy researcherów dla dziennikarskich gwiazd, jest kosztowna. I wszystkie dobre media są w kryzysie finansowym. Na portalu zaś, opinie, może przesyłać byle człowieczek — nie potrzeba mu rozumu, nie marnuje czasu na weryfikację informacji. Musi tylko pisać po linii czytelników. To nie daje jakościowej informacji — nikt tego nie sprzeda za pieniądze odbiorców, wykupujących dostęp (ale już reklamy — owszem, sprzeda) — ale jest to tanie, bo wiele roboty odwalają amatorzy za darmo, ewentualnie stażyści za darmo, lub półdarmo.
wiesiek59 23 CZERWCA 2022 15:42
I niedostosowani zginęli, miliony niedostosowanych Indian zginęło, a niedobitki trafiły do rezerwatów, gdzie sobie się dostosowują do dziś.
PAK4
23 CZERWCA 2022
16:33
Widzisz, najprostszą metodą dotarcia do faktów, jest liczenie trupów.
Prodemokratyczne i „wolnościowe” to dość spory stos od 1945 roku.
Jakieś 40 milionów.
Nie spowodowały tego działania rosyjskie czy chińskie.
Najbardziej mordercze nie są zresztą działania zbrojne, skrytobójstwo czy usadowienie marionetek we władzach większości krajów zależnych od Waszyngtonu.
Najbardziej mordercze są działania ekonomiczne, w pełni kontrolowane przez zachodnie banki i giełdy.
Manipulacje rynkiem energii, zywności, kursami walut narodowych wobec $.
A co do „Polityki”.
Od momentu uzyskania sponsorów, zagranicznych fundacji, zmieniła się linia polityczna, treści w niej zamieszczane.
To miało miejsce jakieś 5-8 lat temu.
Może, od momentu śmierci pani Paradowskiej, której blog był miejscem nieskrępowanych dyskusji na każdy temat.
Od tego czasu klakierzy zajęli miejsce dyskutantów, z pełną akceptacją prowadzących blogi.
Cżęć z nich zajęła się szczuciem zgodnym z najlepszymi wzorcami McCartchyzmu.
Masz tu takie zwierzatka zajmujące się kapowaniem, banowaniem, grzebaniem w przeszłości, insynuacjami,
Rozmnożyło się to tatałajstwo niesamowicie.
Wrociłem w antraktach do lektury 1984.
Bardzo pouczająca i na czasie.
Wprost podręcznik metod zmian świadomości, percepcji mas.
Przepisywanie historii dzieje się na naszych oczach.
A raczej moich.
Ty tego nie dostrzegasz.
ontario
23 CZERWCA 2022
18:54
„Władza deprawuje, władza absolutna deprawuje absolutnie”.
Powierzenie takiej władzy jednostkom ludzkim, elitom zachodu, może skutkować tylko jednym.
Z Ziemi stworzy się Kongo Leopolda.
Bez przeciwwagi, sił zdolnych do neutralizacji presji zysku za wszelką cenę, skończymy jak ci Murzyni pozbawienie ręki za niewykonanie planu.
Na razie, „milczenie owiec”.
Na „folwark zwierząt ” nie ma większych szans, choć być może..?
Owce francuskie, kanadyjskie, spacyfikowano.
Amerykańskie stłamszono.
Brytyjskie się budzą…..
Ps.
Ceny ropy, gazu, zywności, nie są skutkiem niedoborów, tylko SPEKULACJI.
Firmy zajmujące się obrotem tymi towarami notują rekordowe ZYSKI.
Czy dzielą się z rzadami, pracownikami?
Ktoś ma jakieś złudzenia?
olborski
Czytam z uwagą i skupieniem.
Ponieważ nie wiemy ile to potrwa trudno teraz pisać prosto z mostu i jednoznacznie opowiadać się za czyjąś racją. Oni są nieufni, ale my też powinniśmy mieć się na baczności. Granice państw muszą być jasno określone i nienaruszalne.
Są jednak liczne odstępstwa od tej zasady co wielokrotnie tu przypominano, więc nikt nie jest bez winy, a zatem należy pomyśleć zanim rzucimy kamieniem
wiesiek59 23 CZERWCA 2022 19:16
Ja, ja mam złudzenie. Takie oto, że gdy owce pokonają wilki w swoim słusznym gniewie, nie staną się wilkami.
Np. „Solidarność” (owca) po pokonaniu PZPR (wilka) nie stanie się PZPR (wilkiem). Ciągle się łudzę, a to już ponad 30…
ontario
23 CZERWCA 2022
18:54
Jeszcze mała glosa.
Z tego co mi wiadomo, ekspansja portugalska i rosyjska nie zniszczyła żadnego rdzennego narodu.
Również Francuzi postepowali bardziej delikatnie, stawiając na koegzystencję z tubylcami.
Najbardziej brutalni byli Belgowie, Holendrzy, Brytyjczycy.
Sprzeciw= taktyce spalonej ziemi.
Nawet Mongołowie i Kazachowie nie byli tak bezwzględni.
wiesiek59 23 CZERWCA 2022 19:16
Jeszcze średnia glosa.
Modelowy przykład Balcerowicza.
Gdy był owieczką (marksistą z czerwoną legitką), walczył o prawa pracownicze owiec.
Gdy został wilkiem (wicepremierem burżuazyjnego, kapitalistycznego rządu i nie miał już legitki), walczył o prawa wilków do wyrzucania owiec na bruk.
wiesiek59 23 CZERWCA 2022 19:44
Nic mi nie wiadomo o tym, aby jeden kolonizator był bardziej delikatny od drugiego kolonizatora. Coś tam słyszałem np. o kolonizatorach Niemcach i ich ludobójczej polityce w Afryce.
aka.cia 23 CZERWCA 2022 15:31
To, że tu nie ma cenzury nie oznacza, że można tu napisać wszystko. A więc za publiczne zaliczenie mnie do „esbeków”, zgłaszam ten wpis do odpowiednich władz.
ontario
23 CZERWCA 2022
19:40
Nie żartuj.
Frasyniuk, nawiasem mówiąc jeden z sensowniejszych:
„Ludzie mają zap…dalać!!!”……
Daj ludziom władzę, a otrzymasz przewidywalny efekt.
„Żelazne prawo oligarchii” jest aksjomatem.
Nie zmienisz ludzkiej natury.
Fortuny buduje się dzięki bezwzględności, nie litosci.
List wysłany do prokuratury:
Zgłaszam w tym piśmie przestępstwo rozmyślnie popełnione na forum „Polityki” pod adresem „naukowy.blog.polityka.pl/2022/06/18/przeciwko-liczbom-rzeczywistym” przez osobę używającą pseudonimu („nicku”) „aka.cia” dnia 23 czerwca 2022 roku o godzinach 14:37 i 15:31 o następującej treści:
1. 23 CZERWCA 2022 14:37
„Głód w Afryce i krokodyle łzy Zełeńskiego … zamiast na zbrojenia banderowskiej Ukrainy zaopatrzenie Afryki w wodę … ”
Widzę, że Polityka chętnie daje wszelkim faszystom, sowieckim bydlakom, niewydarzonym esbekom oraz innym ofiarom Stomilu wolną trybunę do siania bzdur, nienawiści oraz ruskiej propagandy.
Czy doprawdy parciane, cerowane gacie Matuszki są aż tak atrakcyjne dla szerokiego grona czytelników? Czy kalwaryjskie wodogłowie musi być tu eksponowane 24/7 ?
2. 23 CZERWCA 2022 15:31
kalvarya,
Wykwintnego języka oraz bogactwa wodogłowych myśli, nikt Lesiowi nie odbierze. Z kolei komenda „spadaj” nie działa już tak piorunująco skutecznie jak w złotych dla esbeków czasach. Możesz to teraz wykrzykiwać między szpalerami łóżek w domu starców, ale na blogu prowokuje jedynie do ziewania.
Sorry Lesiu, cuśniecuś w twym żywocie się umoczyło – postawiłeś na kulawego konia, stąd chyba ta deprecha oraz myślowa sraczka. Potrzebujesz więcej miłości, być może wiernego partnera, który codziennie będzie powtarzał: Lechu, ty to jesteś qwa geniusz!
Przestępstwo to polega na publicznym znieważeniu mnie na owym forum, a więc przy użyciu środków masowego przekazu, w tym szczególnie bezpodstawnym nazwaniu mnie „esbekiem”, czyli funkcjonariuszem PRL-owskiej Służby Bezpieczeństwa.
Tak więc zgłaszam do Prokuratury zniesławienie (pomówienie, obmówienie, oszczerstwo) czyli występek polegający na pomówieniu innej osoby o takie postępowanie lub właściwości, które mogą poniżyć ją w opinii publicznej lub narazić na utratę zaufania potrzebnego dla danego stanowiska, zawodu lub rodzaju działalności. Przypominam także, iż ów występek, którego się użytkownik „aka.cia” właśnie dopuścił na forum „Polityki”, jest zagrożony karą grzywny albo karą ograniczenia wolności na podstawie art. 212 § 1 Kodeksu karnego oraz że sprawca podlega grzywnie, karze ograniczenia wolności albo karze pozbawienia wolności do roku jeżeli pomawia inną osobę za pomocą środków masowego komunikowania (art. 212 § 2 k.k.). Przypominam także, iż naruszenie dóbr osobistych, do których zaliczana jest też cześć jednostki, zabrania także Kodeks cywilny w art. 23 i 24, a więc jeśli mnie użytkownik „aka.cia” publicznie nie przeprosi, to wytoczę także jemu oraz redakcji „Polityki” proces cywilny.
Przypominam także, że redakcja „Polityki” pod adresem http://www.polityka.pl/forum/ zamieściła następujący tekst:
„Warto, aby serwis POLITYKA.PL pozostał miejscem wartościowej wymiany poglądów, gdzie toczą się dyskusje, nawet zażarte, ale pozbawione mowy nienawiści. Zależy nam na tym, abyśmy wzajemnie traktowali się z szacunkiem. Chcemy, aby POLITYKA.PL była miejscem wolnym od radykalizmów i anonimowej, bezsensownej brutalności.
Słowem: zapraszamy serdecznie do dyskusji na naszych forach internetowych, do wyrażania opinii, polemik, do ocen, ale w formie przyjętej między kulturalnymi ludźmi. Kto chce się wyżyć – zapraszamy na inne portale. Być może to walka z wiatrakami, ale spróbujemy. Mamy dość językowych i emocjonalnych śmieci zasypujących plac wolności, jakim miał być i może być internet.”
Cytowany przeze mnie wpis użytkownika „aka.cia” jest także niezgodny z Regulaminem Forum „Polityki” oraz Zasadami Publikowania Komentarzy na forum „Polityki”, które są zamieszczone pod adresem http://www.polityka.pl/opolityce/1508316,1,zasady-publikacji-komentarzy.read a które wyraźnie stwierdzają co następuje:
„1. Zapoznaj się dokładnie z Regulaminem serwisu i przestrzegaj jego zasad.
2. Pamiętaj, że nie jesteś anonimowy w sieci. Ponosisz odpowiedzialność prawną za swoje wypowiedzi, które naruszają dobra osobiste innych osób. Twoje wpisy naruszające zasady komentowania i Regulaminu będą usuwane. A w szczególności te, które:
a. Zawierają groźby, treści wulgarne, obsceniczne, nienawistne, agresywne, dyskryminujące i inne tego rodzaju;
b. Obrażają i deprecjonują inne osoby ze względu na ich pochodzenie, wykonywany zawód, przekonania, wyznanie, światopogląd, wiek, płeć czy orientację seksualną;
c. Dotykają prywatności innych osób, naruszają ich godność, dobra osobiste, prawa autorskie i inne dobra prawem chronione;
d. Zawierają oskarżenia, które nie są podparte dowodami w postaci ustaleń prokuratury czy wyroków sądów;
e. Są niezgodne z obowiązującym prawem, zasadami współżycia społecznego i dobrymi obyczajami;
f. Zawierają wiadomości z prywatnymi adresami poczty elektronicznej, danymi osobowymi i teleadresowymi innych osób;
g. W odniesieniu do innych uczestników dyskusji posługują się nazwiskiem, zamiast nickiem lub imieniem.”
Ponadto, to pod adresem http://www.polityka.pl/opolityce/1500085,1,regulamin-korzystania-z-serwisu-politykapl.readjest wyraźnie napisane, że: „Korzystanie z Serwisu wymaga przestrzegania postanowień właściwych regulaminów. Warunki uczestnictwa w forum dyskusyjnym udostępnianym w Serwisie pod adresem URL forum.polityka.pl określa Regulamin uczestnictwa w forum internetowym”.
Calvin Hobbs 23 CZERWCA 2022 17:10
USA napadły na Koreę, aby nie dopuścić do zwycięstwa komunistów w wolnych, uczciwych wyborach. 🙁
Natomiast bezpardonowy atak na Autora tych publikacji i prof. Kieżuna (,,Patologia
transformacji’’) (Kieżun, 2012) przeprowadzony został w owym czasie w Internecie przez
jednego z czołowych polskich ekonomistów wykładających za granicą. Rzeczowych
argumentów nie zauważyłem – był to atak ,,ideologiczny’’ i ,,polityczny’’.
Krytycznych publikacji odnośnie do polskich reform prywatyzujących gospodarkę jest
więcej. Bodaj najbardziej udokumentowaną pozycją opierającą się o dokumenty źródłowe jest
praca Ryszarda Ślązaka ,,Czarna księga prywatyzacji 1988-1994, czyli jak likwidowano
przemysł”(Ślązak, 2016).
Szczegółami i dokładną chronologią wydarzeń imponuje książka Pawła Bożyka
,,Apokalipsa według Pawła. Jak zniszczono nasz kraj’’ (Bożyk, 2015).
Na szczególne wyróżnienie zasługują też prace Andrzeja Karpińskiego z Zespołem, na
które będę powoływać się w treści prezentowanego referatu.
http://www.pte.pl/pliki/2/12/jakubowicz_nowy_26.pdf
kalvarya01
23 CZERWCA 2022
19:52
Nie można tolerować mowy nienawiści.
Przypominam jednak, że właśnie na forach „Polityki” jeden z zawołanych redaktorów (Szostkiewicz) mowę nienawiści na forum nazwał facecjami. Toleruje te facecje, akceptuje nazywanie ludzi gnidami i mendami, zob. wpisy Szostkiewicza na swoim forum.
wiesiek59
23 CZERWCA 2022
19:51
Zdrów strój sobie żarty!
Frasyniuk (owca) stał się wilkiem. Fortuny buduje się, będąc wilkiem, ale natura ludzka się zmienia, bowiem owca może stać się wilkiem, np. Frasyniuk, Balcerowicz.
Nie prywatyzacja, a raczej reprywatyzacja, ale taka, w którym znacjonalizowane dobra dano komu innemu niż pierwotnym właścicielom. Klasyczny wyjątek to oddanie majątku klerowi, oddanie przez komunistów.
https://tadeuszczernik.files.wordpress.com/2014/06/kiec5bcun-w-patologia-transformacji.pdf
=========
Kieżun, do poczytania.
Długi tekst- uprzedzam.
wiesiek59 23 CZERWCA 2022 20:21
Nie czytam, bo wiem, co się działo.
Jakże wielce budujący jest przykład Jachiry!
Ostatnio widowiskowo protestowała przeciwko sobie samej, bo wzięła znaczącą podwyżkę z budżetu państwa, podczas gdy milionom Polaków takowej podwyżki nie przyznano.
ontario 23 CZERWCA 2022 20:08
Bo on sam jest zwolennikiem mowy nienawiści… :-(
ontario 23 CZERWCA 2022 20:26
Lewaczka bez honoru. 🙁
ontario
23 CZERWCA 2022
20:14
Polska opozycja polityczna była wsłuchana- tak jak i ja- w Głos Ameryki, czy Wolną Europę.
„Nigdy deszcz nie pada w Californii
Tam banany leca z nieba tak jak deszcz”…..
Tyle że nasza koncesjonowana opozycja otrzymywała dotacje.
Na koniaki z Pewexu….starczyło aż nadto.
Ile to kosztowało?
100 milionów z CIA, 100 z Watykanu.
Za przejęcie kraju, tanio jak barszcz.
Nie rozwlekając zbytnio.
Jesteśmy tu, gdzie jesteśmy, wraz z elitami sponsorowanymi z zewnątrz i decyzjami podjętymi w imieniu nas.
I musimy PRZEŻYĆ te decyzje.
Albo i nie….
Owce mają niewielki wybór uniknięcia rzeźni.
PAK4 23 CZERWCA 2022 18:47
1. Wszystkie źródła, które ty cytujesz, to są tylko źródła opinii a nie źródła informacji, a to jest bardzo istotna różnica.
2. Kapitalizm polega na wyzysku, oszustwach i redukcji kosztów w celu maksymalizacji zysków garstki bogaczy a wszystkie media są dziś w kryzysie finansowym, tak jak cały globalny kapitalizm.
Tyle że nadwiślańskie Eldorado okazało się prawdziwe. Przykładowo opisuje Kieżun, jak belgijski koncern SBFRF dostał w 1990 r. ofertę zakupu nowoczesnej i potężnej Cementowni Górażdże na raty po 15 mln rocznie, czyli za równowartość rocznego zysku firmy. Oburzyło to załogę i pod wpływem jej protestów umowę anulowano. Jednak trzy lata później 30 proc. akcji cementowni za przeszło 90 mln marek i zobowiązanie kontynuacji działalności kupiła inna belgijska spółka – CBR Baltic. Złamała jednak umowę już dwa miesiące po jej zawarciu, sprzedając cementownię niemieckiemu Heidelbergerowi. Rząd polski nie interweniował. W podobny sposób sprzedano zagranicznym inwestorom 16 polskich cementowni. A mogły one być tanim zapleczem dla budowy w Polsce dróg i autostrad, za które tak bardzo od lat przepłacamy. Zamiast tego stały się źródłem wysokich zysków zachodniego kapitału.
https://teologiapolityczna.pl/bartlomiej-radziejewski-iii-rp-czyli-nowe-kondominium-zachodu
wiesiek59
23 CZERWCA 2022
20:33
W naszej Polsce od zarania obowiązuje prawo wilków w stosunku do owiec. Prawo to umiejętnie sformułował liberał, demokrata, postępowiec (słowem, wilk w owczej skórze) Tusk: „To nie są wasze pieniądze”.
Ani ty nie masz, ani ja nie mam, ani żadna owca nie ma własnych pieniędzy (majątku, dóbr itd.) wypracowanych przez pokolenia owiec. Nasze pieniądze (dobra, majątki itd.) mają wilki.
kalvarya01
23 CZERWCA 2022
20:34
Fakty sa łatwo weryfikowalne.
Rozpieprzono ekonomię kilkudziesięciu krajów.
Zamordowano kilkuset przywódców
Zrobiły to kraje DEMOKRATYCZNE w imię interesów swoich korporacji.
Nie ma na to usprawiedliwienia.
Szczególnie biorąc pod uwagę dziesięciolecia chaosu na tych terenach.
Teraz skutki sięgają rykoszetem Europę.
A jej elity nie sa w stanie intelektualnie garnąć tematu.
Intelekt Forresta Gumpa był wyższej klasy?
wiesiek59
23 CZERWCA 2022
20:37
Co ta wiedza o tym, co się działo na naszych owczych oczętach daje? Nic!
Mądrzejsze owce wybrały ucieczkę z owczarni, np. do obcych wilków, choćby i nawet im przyszło podcierać zadki tychże wilków. Zawsze lepiej wyszły te owce na tym podcieraniu, jakby zostały w Polsce na etacie doktora czy nauczyciela itd..
ontario
23 CZERWCA 2022
20:42
Cóż, homo homini lupus w ponoć katolickim kraju, to oczywistość.
Media zrobią ten temat na odwyrtkę….
PAK4 23 CZERWCA 2022 16:33
1. Zdrowy rozsądek mówi nam, że Ziemia jest płaska a Słońce krąży wokół niej.
2. Ja nie mam „własnych” źródeł a tylko korzystam ze statystyk OECD, IMF (MFW), World Bank (Banku Światowego) etc., a ty podajesz nam tylko swoje własne opinie i powtarzasz kłamstwa reżimowej propagandy.
3. Giełda to jest kasyno.
4. W realnym kapitalizmie NIE ma bezstronnych mediów na starej szkockiej zasadzie, że „who pays the piper calls the tune”.
5. Powiązanie między sponsorem a wymogiem pisania pod jego dyktando jest dziś największe na tzw. Zachodzie.
6. Polska wygląda dziś bardzo ładnie – tak jak trup przygotowany do pochówku przez dobrych „trumniarzy” czy też raczej „trupiarzy”.
7. Na temat wojny na Ukrainie nie mamy w polskojęzycznych mediach informacji, a tylko nachalną i prymitywną pro-banderowską propagandę. 🙁
wiesiek59 23 CZERWCA 2022 20:45
TAK. Ale to do PAK4 NIE trafi… 🙁
ontario
23 CZERWCA 2022
20:47
Swego czasu uważałem, że czytelnicy Polityki i jej blogowicze to bystrzachy w stosunku do reszty spoleczeństwa.
Staranna selekcja na wielu blogach autorskich skłania do innej wersji.
Dlaczego banuję?
Bo MOGĘ…..
To nie jest ego, to WYTYCZNE.
W ten sposób łamie się kręgosłupy dziennikarzom.
@PAK4
„Ekhm… Przy okazji „Polski w ruinie”, znanego hasła, znanej partii, to moja żona sobie kpiła, że wystarczy zerknąć za okno by sprawdzić jaka jest prawda.”
Umhmm…A jakiej wypasionej bryki było to okienko?
W dawnych czasach, przy okazji „socjalizmu w ruinie” jakiś bonza ze znanej wówczs aż a dobrze partii, wyglądajac przez okno czarnej wołgi powiadał do współpasażera:
-Wiecie co towarzyszu, przez okno czarnej wołgi to nawet socjalizm wygląda całkiem nieźle.
Podobno Rosjanie wznawiają produkcje wołgi. Czyżby Pani PAK4 miała jakieś dojścia?
wiesiek59
23 CZERWCA 2022
20:48
Katolicki kraj jest katolickim krajem z nazwy. Jeśli już ktoś tu jest katolikiem, to nieduży % owiec i niektórzy nieliczni pasterze.
wiesiek59
23 CZERWCA 2022
20:54
Dziennikarze „Polityki” i kręgosłup? To sprzeczność sama w sobie. Wystarczy przypomnieć, co o nich napisał Szymon Kobyliński, niestety, w przypływie szczerości, gdy już odchodził z „Polityki”. Biedaczek, otworzyły mu się oczęta, gdy już był poza kręgiem „Polityki”.
kalvarya01
23 CZERWCA 2022
20:27
Raczej kiepska baletnica w cyrku, nadrabia miną.
wiesiek59 godz. 20.37
To normalny scenariusz kapitalistów. Taki tani łup po 1989 roku.
Wystarczy propaganda i obietnice.
Rozdzielić, rozparcelować i zarządzać.
Co teraz mówią załogi tych cementowni?
O wzroście zadłużenia niechętnie piszą rządowe media.
kalvarya01
23 CZERWCA 2022
20:27
Jest zwolennikiem facecji oraz bojownikiem o wolność słowa, ale wolności dla takich, jak on.
Można by to nazwać dulszczyzną, ale to raczej Dulska mogłaby u niego pobierać korepetycje.
ls42
23 CZERWCA 2022
21:12
Postawiłbym inne pytanie. Ilu pracowników cementowni wyjechało do kapitalistów (na Zachód), aby wykonywać najgorsze prace, zawsze jednak lepiej opłacane niż najlepsze zajęcia w peerelowskich cementowniach?
@wiesiek59
23 czerwca 2022
20:54
„W ten sposób łamie się kręgosłupy dziennikarzom.”
Dzisiejszym dziennikarzom nie da się złamać kręgosłupa — jest zbyt giętki. To wynik starannego doboru hodowlanego. Tyle że na Zachodzie zajął ten proces kilka pokoleń selekcji, w Polsce po ’89 zaledwie paręnaście lat! Imponujące! Dzisiaj dziennikarzowi nie trzeba żadnych wytycznych z zewnątrz. On czuje pismo, które ma napisać, jakimś szóstym zmysłem. Ma to w genach?
Kiedyś, ktoś z branży (z Zachodu) wyraził to w następujący sposób. Dzisiaj korupcja w mediach nie polega na tym, że przychodzi ktoś z polityki albo biznesu i płaci dziennikarzowi za napisanie jakiegoś steku łgarstw.
Teraz to dziennikarz gotów jest zapłacić, żeby mu pozwolono taki stek wysmażyć.
Oczywiście bywają wyjątki. Ale ci świetnie się maskują.
„Świdryga z Mitrygą”
To poezja Leśmiana przypomniana w telewizji w programie „Milionerzy”.
Jesteśmy niestety nadal w czołówce pijących.
A tyle razy przestrzegano przed spożyciem, szczególnie kierujących pojazdami. W czasach Bolesława Leśmiana (1877-1937) polskich kierowców zbyt wielu nie było, zatem chodziło poecie z pewnością o całokształt
ontario 23 CZERWCA 2022 21:12
Niewątpliwie.
PAK4 23 CZERWCA 2022 15:20
1. To raczej ty szerzysz, jako prawdę, tekściki z firemki z ograniczoną odpowiedzialnością kierowaną przez wysoką szychę w kontrolowanych przez POPiS i CIA władzach RP.
2. Swoją drogą, to finanse Polityki, czy Guardiana są tak przejrzyste jak finanse mafii. To są media zależne od sponsorów i central wywiadowczych, tak jak praktycznie wszystkie wysokonakładowe pisma czy popularne stacje radiowe i telewizyjne. Pokaż mi na tzw. Zachodzie poważnego publikatora, który utrzymuje się tylko ze sprzedaży pisma czy też nadawania programu, bez uzależnienia się od reklam czyli od kapitału albo od rządu.
3. Rosja zaatakowała w samoobronie, uprzedzając wejście Ukrainy do NATO i utworzenie tam baz USA.
4. To co tu piszesz, nie trzyma się kupy. Nic z tego co piszesz, nie wiąże się logicznie z usprawiedliwieniem inwazji USA na Koreę, Wietnam, Irak czy Afganistan – zostawiam na boku to, że 99% tego co piszesz, to są zwyczajne kłamstwa. Kłamać jest tobie łatwo, ale prostowanie twych kłamstw to wcale nie jest ciężka praca, gdyż ja na sprawdzanie, weryfikowanie i prostowanie twoich kłamstw mam dość sił.
5. Zrób najpierw, tak jak ja, PhD na uczelni z czołówki światowej, a później mów tu o „research”.
6. Gdzie i kiedy miałeś ten „osobisty kontakt z procesem przyznawania środków na rozwój technologiczny polskich firm z pieniędzy unijnych”? Jako (były z powodów wyjaśnionych uprzednio) ekspert KE ma na ten temat inną wiedzę i to prosto z Brukseli. Gdzie masz zresztą dziś polską high tech?
7. Powtarzam – lobbing to jest po prostu przekupywanie i korumpowanie polityków. Tylko ich wyborcy powinni mieć do nich dostęp, i tylko ich głosu powinni politycy słuchać, a nie glosu pieniędzy lobbystów.
8. Tak, niebawem światem będą rządzić Chiny, India i Rosja, gdyż Zachód sie po prostu cofa, skrepowany gorsetem politycznej poprawności, ekologizmu, genderyzmu etc. i pod ciężarem swego zadłużenia.
Powinno być „Świdryga z Midrygą”
A w tym przypadku chodziło o taniec z dziewczyną, co niestety tych mężczyzn doprowadziło do śmierci.
Dalszą interpretację wiersza Leśmiana pozostawiam literatoroznawcom.
Poza liczbą osób w wierszu, i 20 tys. złotych za poprawną odpowiedź, reszta jest poza tematem zagajenia, niemniej przypomnienie przesłania poety uważam za uzasadnione na blogu naukowców, bowiem wszystko kończy się śmiercią
eche
23 CZERWCA 2022
21:30
Czyżby w PRL-u (zatem przed 89) dziennikarze mieli kręgosłupy? W jakich pismach, skoro niemal wszystkie pisma były rzecznikami PZPR pod szyldem „Proletariusze…”?
W „Polityce” dotąd jeszcze się nie uporali z zamazaniem szyldu, prześwituje przez czerwoną farbę.
kalwaryo,
Tak bardzo bym chciał cię w żalu utulić, przez ulicę przeprowadzić albo pomóc włożyć piżamę. Ale tyś chyba za daleko, w Koluszkach albo jeszcze dalej.
Wiadomość o prokuraturze przyjąłem z ogromną radością, myslę, że prokuratura również będzie zachwycona. Jest już nb. wyznaczona ekipa: sędzia – miszauszatek59, oskarżyciel – gienek z wałcza oraz świadkowie: jadurny kowalski, kaganbezpiór 1.00 oraz polska komunistyczna 2.00
Ale będzie się działo!
@wiesiek59 23 czerwca 2022 20:37
Tyle że nadwiślańskie Eldorado okazało się prawdziwe. […] W podobny sposób sprzedano zagranicznym inwestorom 16 polskich cementowni. […] Zamiast tego stały się źródłem wysokich zysków zachodniego kapitału.
Thomas Piketty w „Time For Socialism”, rozdział „2018:The Year of Europe”, str. 165, zamieścił wykres pokazujący bilans przypływu i odpływu pieniędzy krajów Europy Środkowej – Polski, Węgier, Czech i Słowacji w latach 2010 – 2016. Dla każdego z nich był on ujemny, tj. odprowadzanie zysków z zachodnich inwestycji w produkcję i nieruchomości znacznie przekraczało dotacje Unii Europejskiej. Dla Polski w tym okresie odprowadzone zyski to 4,7% PKB, podczas gdy dotacje to 2,7% PKB, czyli -2%. To i tak nieźle w porównaniu z Czechami (zyski 7,6%, dotacje 1,9%, -5,7).
Czy dziennikarstwo za pieniądze jest misją … Tak sobie myślę prywatnie … kolejny mit … jak order od papieża dla sędziego za pobożne wyroki …
Banderowcy zastrzelili członka swojej delegacji na rozmowy w Mińsku … a świat milczy … Tak sobie myślę prywatnie … potraktowano sprawę jak wypadek przy pracy … Obama zabijał przy pomocy pilota w zagranicznych akcjach … podobnie Trump …
Może nie na temt tego blogu:
Najważniejsze cechy kościoła rzymsko-katolickiego:
1. Pycha
2. Chciwość
3. Nieczystość
4. Zazdrość
5. Nieumiarkowanie w jedzeniu i piciu
6. Gniew
7. Lenistwo
https://wiadomosci.gazeta.pl/wiadomosci/7,114883,28616285,poznan-rzucila-jajkami-w-drzwi-kosciola-sad-uznal-ze-obrazila.html#s=BoxLoCpMT
Dalej off subject:
Po raz kolejny Rosjanom udało się dokonać w krótkim czasie zauważalnych postępów podczas walk w Donbasie. Zajęli spory, jak na realia obecnych walk, teren na południe od Lisiczańska.
Komentarz z „Wybiórczej”- nie mój:
Ukraińcy nieco padli ofiarą własnej propagandy, trzeba oddać sprawiedliwie przy aplauzie zachodnich mediów, gdzie rosyjscy siepacze byli przedstawiani jako słabo zorganizowaną armię, słabo zaopatrzoną, słabo uzbrojoną, gdzie masowo zostawiają sprzęt i dezerterują. W zachodnich mediach co chwila pojawiały się hurraoptymistyczne komentarze, że Rosja już przegrała. Oczywiście pojawili się różni emerytowani generałowie, jak np. Skrzypczak, którego doświadczenia frontowe to głównie rola namiestnika w okupowanym Iraku, który nie tak dawno mówił o walkach w Donbasie:
„Były dowódca Wojsk Lądowych generał Waldemar Skrzypczak zapytany w wywiadzie dla „Super Express” o to, kto obecnie wygrywa wojnę, odparł: – Ukraińcy.”
Niestety, co prawda agresorom ruskim jest daleko do wyobrażeń o swoich siepaczach Putina, to nie są tak beznadziejni, jak to przedstawia to propaganda ukraińska, czy zachodnia. Ukraińskim żołnierzom w Donbasie morale zaczyna spadać, bo niestety ruskie mają przewagę, przede wszystkim w artylerii, i oni są cały czas pod obstrzałem, na który niespecjalnie mają czym odpowiedzieć.
Co na to PAK4?
Donbas to Rosjanie … to narodowa porcelana … Tak sobie myślę prywatnie … dlaczego wojskowi mają tłuc swoją porcelanę … zostawmy to słoniom …
A teraz do PAK4 o USA ad Senat uchwalił reformę prawa do posiadania broni :
Jaka „radykana zmiana”? Jak oni chcą weryfikować te osoby? Jak oni zweryfikują, że uczeń jest potencjalnie niebezpieczny? Wszyscy ci szkolni mordercy wyglądali na normalnych. Bzdura. A przestępcy i tak będą mieli broń. To chory kraj, bo jak kraj, w którym posiadanie broni jest podstawowym prawem obywatela, może być normalny. Tam jest za dużo świrów i tradycji dzikiego zachodu. Wystarczy popatrzeć na ich filmy – same strzelaniny i wymachiwanie pistoletami.
Ja poszedłbym dalej. Dlaczego są jakiekolwiek ograniczenia (po za finansowymi oczywiście) w dostępie do jakiejkolwiek broni? Przecież każdy obywatel powinien mieć prawo o ile go stać kupić sobie czy to ręczne wyrzutnie rakiet czy też zaawansowane systemy rakiet np. takie jak przekazano na Ukrainne czy też posiadać prawo do posiadania własnej broni czy to chemicznej czy to biologicznej. Bron jest broń i nie powinno być ograniczeń w jej dostępności.
9 mm w prezencie na chrzciny, a na komunię to co najmniej kałach. Ewentualnie zamiast quada to pickup z zamontowanym na pace działkiem.
https://wiadomosci.gazeta.pl/wiadomosci/7,114881,28616889,senat-usa-uchwalil-reforme-prawa-do-posiadania-broni-pierwsza.html#s=BoxOpImg5
ontario 23 CZERWCA 2022
W PRL-u (a zatem przed rokiem 1989) dziennikarze mieli tak samo „flexible” czyli giętkie kręgosłupy jak dziś, tyle że wówczas lewo- a dziś, jak za Sanacji, prawo-stronnie wygięte.
@kalvarya01:
> To, że tu nie ma cenzury nie oznacza, że można tu napisać wszystko. A więc za publiczne zaliczenie mnie do „esbeków”, zgłaszam ten wpis do odpowiednich władz.
Dzięki. Potwierdzasz moją obserwację, że czym kto głośniej awanturuje się o „wolność słowa” i „walczy z cenzurą”, tym większym zamordystą i zwolennikiem cenzurowania jest.
> To są media zależne od sponsorów i central wywiadowczych
A więc Pan nadal nic nie wie, nie rozumie i nie chce wiedzieć.
> jako (były z powodów wyjaśnionych uprzednio) ekspert KE
Jako aktualny ekspert NCBiR i PARP, odpowiadam jak wyżej.
Swoją drogą, na stronie uczelni nie piszesz, że jesteś „byłym” ekspertem, tylko sugerujesz, że aktualnym. Ale… czepiam się drobiazgów.
> Nic z tego co piszesz, nie wiąże się logicznie z usprawiedliwieniem inwazji USA na Koreę, Wietnam, Irak czy Afganistan
Szanowny Pan odbijać raczy piłeczkę i cytować (plagiat! 😀 ), tyle że bez sensu, bo nigdzie tu tematem nie były inwazja na Wietnam (czyja?!), Irak, czy Afganistan. O Korei, owszem, ale to Koreę Południową zaatakowała Północna, czego zresztą nie nigdy usprawiedliwiałem…
> Ja nie mam „własnych” źródeł a tylko korzystam ze statystyk OECD, IMF (MFW), World Bank (Banku Światowego) etc., a ty podajesz nam tylko swoje własne opinie i powtarzasz kłamstwa reżimowej propagandy.
1) Hm… jakie źródło — OECD, IMF, czy Bank Światowy twierdziło, że chińskie samochody mają lepszą opinię od amerykańskich? Jakie twierdziło, że Chiny mają rozwinięte technologie silników lotniczych, tylko to utajniają?
2) Tak, często podaję opinie…
a) Ale mój ogląd ulic, rozmowy, filmiki na YT (które wyśmiewam, a których słucham) np. przekonują, że Tesla ma w Polsce większe wzięcie niż Xpeng. Takich zasięgów osobistego doświadczenia jest dużo więcej. Nie wspominając o tym, że jeżdżę Fordem (co z tego, że z fabryki w Kolonii), więc mogę to odczuć jako osobistą zniewagę 😛
b) Podobnie jak przebytych lektur, których nie chce mi się przytaczać, bo za dużo roboty. O robocie zresztą dalej…
c) Jak w przypadku śledztw, czy badania przyczyn wypadków stosuje się zasadę ekonomii. Potrafię dotrzeć do statystyk, czasem je sprawdzam. Robię to jednak tylko wtedy, gdy uważam za konieczne. Nie potrzebuję statystyk OECD by wiedzieć, że Rosja napadła na Ukrainę bez usprawiedliwienia — choćby dlatego, że Was czytam 😀 Podajecie nie argumenty, nie fakty, tylko opinie, zabarwione niechęcią, by nie powiedzieć nienawiścią do Zachodu i bezprzykładnym oddaniem do Wschodu. Jak polemizować z zabarwieniem emocjonalnym? Mam Wam wyciągać statystyki, że przeciętny kalifornijczyk żyje dłużej i zdrowiej niż przeciętny Rosjanin? Coś to zmieni w Waszych głowach? Przecież sami wiecie, że nie o to chodzi.
d) No i właśnie — pewna filozofia. Może zacznę od tego, że tak jak Ty, mam skłonność do nominalizmu (czyli przeciwko Husowi, a za tradycją średniowiecznej filozofii niemieckiej 😀 ). Wszystko co piszecie, to taki czarno-biały obraz świata, gdzie dobre Yang Wschodu walczy ze złym Yin Zachodu. Ja, po pierwsze, nie wierzę w dualistyczny obraz świata; ale też po drugie, tak serio przyciśnięty, że albo Biden, albo Putin, to wybiorę Bidena — bo — filozoficznie — blisko mi do ideałów wolności, równości i siostrzeństwa, czyli całego tego spadku ideałów europejskiej lewicy, które na Zachodzie są realizowane ułomnie, ale których realizacji poza Zachodem nie da się doszukać.
@eche:
> Umhmm…A jakiej wypasionej bryki było to okienko?
Wiejskiego domu teściów, na pół-głębokiej prowincji. ‚
Czy serio masz tak grube okulary ideologii by tego nie widzieć?
ls42 23 CZERWCA 2022 21:57
“In the long run we are all dead.” These unforgettable words by John Maynard Keynes have had an unbelievable influence on subsequent economic thought, public policy, and political history. This is largely justified because he was one of the giant thinkers of the past century.
„Nothing is certain but death and taxes” is a proverb that means one cannot avoid the inevitable, that certain things in life are common to all men and cannot be avoided. A man may not escape death, and a man cannot escape paying taxes. The origin of the phrase is generally attributed to Benjamin Franklin.
Po naszemu:
„W dłuższej perspektywie (czasu) wszyscy jesteśmy (będziemy) martwi”. Te niezapomniane słowa Johna Maynarda Keynesa wywarły niewiarygodny wpływ na późniejszą myśl ekonomiczną, politykę publiczną i historię polityczną. Jest to w dużej mierze uzasadnione, ponieważ był on jednym z największych myślicieli minionego stulecia.
„Nic nie jest pewne oprócz śmierci i podatków” – to przysłowie oznacza, że nie można uniknąć tego, co nieuniknione, że pewne rzeczy w życiu są wspólne dla wszystkich ludzi i nie można ich uniknąć. Człowiek nie może uniknąć śmierci, nie może też (w teorii przynajmniej) uniknąć płacenia podatków. Powszechnie przypisuje się pochodzenie tego przysłowia Benjaminowi Franklinowi.
Miłość Bliźniego, to fundament chrzescijańskiej ideologii.
Jak była realizowana ta koncepcja na przestrzeni wieków?
Podobnie jest z demokratyzacją świata, prawami człowieka.
Jakie są efekty?
Słowa są szlachetne, idee wzniosłe.
Tylko czyny przeczą słowom.
Niestety, lemingi nie widzą różnicy, są regularnie okłamywane przy urnach wyborczych i akceptują to.
Zbawianie świata gdzieś na antypodach i coraz większy burdel we własnym domu.
Wydawanie miliardów kreowanych z powietrza za granicą, zamiast w kraju?
Jaka w tym logika?
Jeszcze mocniejsze jest:
we are all ALREADY dead.
(so spread joy, not doubt).
Taki trudny stoicyzm przydalby sie ludzkosci i kazdemu z nas z osobna.
Ale coz skoro jestesmy dziecmi we mgle…
PAK4 24 CZERWCA 2022 8:16
1. Odróżnij cenzurę od usuwania wpisów naruszających prawo. Co byś powiedział, gdybym na tym forum napisał, że powiedzmy Jan Kowalski z Pcimia Średniego, Aleja Lecha Kaczyńskiego 1 m. 1, używający nicka „PAK4” jest znanym pedofilem? I dlaczego popierasz mowę nienawiści? Na zasadzie tzw. moralności Kalego?
2. Pokaż mi prawdziwie niezależne pismo, czy stację radiową albo telewizyjną.
3. Byłem też do niedawna ekspertem NCBiR i PARP a więc wiem, że są to sa instytucje powołane do rozdzielania pieniędzy podatników pomiędzy „krewnych i znajomych królika”. Pokaż mi też ten współczesny polski przemysł wysokiej technologii (high tech).
4. Na internecie są też moje stare CV, których nie jestem w stanie zaktualizować, gdyż nie możliwości ich aktualizacji.
5. To ty „odbijasz piłeczkę”, nie mogąc zaprzeczyć, ze USA to jest współczesne Imperium Zła, które zaatakowało m. in. Koreę, Wietnam, Irak i Afganistan. Nic z tego co piszesz, nie wiąże się też logicznie z usprawiedliwieniem inwazji USA na Koreę, Wietnam, Irak czy Afganistan. W Korei chodziło o to, aby do władzy nie doszli komuniści, w Wietnamie aby obalić władzę komunistów na północy, w Iraku o ropę naftową i Iran a w Afganistanie o opanowanie strategicznie bardzo ważnego terytorium a także wcześniej o obalenie władzy komunistów. Podobnie było np. w Chile, i na Kubie.
6. Nie ma godnych zaufania statystyk jakości samochodów czy samolotów, ale wiadomo, że najlepsze samochody są japońskie a później niemieckie a najgorsze amerykańskie (mowa o samochodach dla „ludu”, a nie o najdroższych, luksusowych limuzynach dla elity). Dawniej samoloty made in USA były najlepsze, ale ostatni naprawdę udany ich model to B747 czy Jumbo Jet. Tesla produkuje zaś szmelc dla wykształciuchów i „enwironmentalistów”. W Polsce nie kupuje się też samochodów na „F” czyli „Fordów”, „Fiatów” i „Francuskich”. ;-)
7. Rosja nie napadła na Ukrainę, to Ukraina swoją polityka dyskryminacji Rosjan i dążeniem do NATO zmusiła Rosję do tej interwencji. Podobnie zresztą USA usprawiedliwiły swoje poparcie dla Pinocheta tym, że musiały to zrobić, bo inaczej to Chile znalazło by się w RWPG i Układzie Warszawskim.
8. To my, czyli twoi adwersarze, podajemy fakty, a ty tylko opinie, zabarwione niechęcią, aby nie powiedzieć że wręcz nienawiścią do Wschodu i bezprzykładnym oddaniem do Zachodu, zapominając, że Polska leży w Europie Wschodniej, a nie Zachodniej i że rasistowski i szowinistyczny z natury Zachód wciąż uważa nas za pariasów. Co to też znaczy, że przeciętny Kalifornijczyk żyje dłużej i zdrowiej niż przeciętny Rosjanin? Jak te statystyki definiują termin „zdrowiej”? Poza tym, to średnia arytmetyczna nic nam nie mówi – np. ja zarabiam milion złotych na rok a ty złotówkę. Średnio zarabiamy więc, według mojego komputera dokładnie 500000 złotych i 50 groszy. Słyszałeś może coś o odchyleniu standardowym, medianie czy dominancie? Ostatecznie to jest blog osób uważających się za naukowców! Ale czy to coś to zmieni w twojej głowie? Obawiam się że NIE… :-(
9. Filozofia, tak jak teologia czy matematyka NIE jest nauką. I to przecież u ciebie, tak jak np. w „Wyborczej”, „Polityce”, TVP, TVN, BBC, CNN, DW etc. jest ten czarno-biały obraz świata, gdzie dobre Yang Zachodu walczy ze złym Yin Wschodu, gdzie dobry czyli zachodni Ormuzd czyli Ahura Mazda walczy ze złym, czyli wschodnim Złym Duchem Ahrymanem (Angra Mainju). To jest zresztą piękna bajka: „Na początku (Bereszit) były dwa duchy: Ormuzd (Ahura Mazda) i Ahryman (Angra Mainju). Ormuzd przebywał w górze, w nieskończonym blasku. Ahryman w dole, w mroku nieprzeniknionym. Wszystko co dobre – mądrość, prawość, jasność, piękno – zawarte było w Ormuździe, wszystko co złe w Ahrymanie. I tak było od nieskończoności. Aż wydarzyło się, że promień blasku przeniknął mrok i Ahryman poznał, że nie jest sam, że jest jeszcze coś innego. Przyciągnięty blaskiem podążył w górę i chciał ową jasność pochwycić. Ormuzd jednak przemądry rzucił w niego słowem modlitwy, które odebrało siły Władcy Ciemności, tak że spadł On w przepaść i przebywał tam przez trzy tysiące lat.
Ja np. piszę krytycznie też o chińskim, nie tylko o amerykańskim zamordyzmie, ale ty nigdy nie krytykujesz zachodniego czy też izraelskiego rasizmu, szowinizmu, militaryzmu, kolonializmu, ekspansjonizmu etc. etc.
10. Ty popierasz realny kapitalizm rynkowy, ktory z definicji nie ma nic wspólnego z lewicowymi ideałami wolności, równości i braterstwa/siostrzeństwa/obojnactwa. To jest dziś wciąż, tak jak to Arkady Fiedler opisywał jak to w praktyce wyglądała na Madagaskarze implementacja ideałów Rewolucji Francuskiej, czyli liberté, égalité, fraternité – podatek pogłówny, aby zmusić tubylców do pracy na rzecz kolonizatorów, wszystkie stanowiska we władzach tylko dla białych i de facto apartheid, tak jak dziś w Palestynie – nielegalnie okupowanej przez Izrael przy pomocy USA i Niemiec.
Szalom!
@Wiesiek59:
> Miłość Bliźniego, to fundament chrzescijańskiej ideologii.
Jak była realizowana ta koncepcja na przestrzeni wieków?
Powiedziałbym, że nie najgorzej.
Krytykujesz rzeczywistość, ale zestawiasz ją z tym, jak było przed ową „miłością bliźniego”?
Chciałem Ci napisać, że 100 lat temu nie było płatnych urlopów, ale sprawdziłem — właśnie 100 lat temu w je w Polsce wprowadzono. Wielu rzeczy, które ułatwiają nam życie, dając to minimum warunków sensownego, zdrowego funkcjonowania: płatny urlop, powszechna opieka zdrowotna, powszechny obowiązek szkolny, wraz z szansami edukacyjnymi, zmniejszenie poziomu przestępczości, przy jednoczesnej humanitaryzacji prawa (zmniejszenie kar, likwidacja kary śmierci itp.); zmniejszenie liczby konfliktów międzynarodowych; zniesienie barier ze względu na płeć, pochodzenie (klasę społeczną), zwiększono mobilność społeczną… można by długo… kiedyś nie było, a są. Są, bo idealiści wierzący w prawa człowieka, obywatela i miłość bliźniego naciskali, protestowali, a czasem nawet oddawali życie.
> Słowa są szlachetne, idee wzniosłe.
Tylko czyny przeczą słowom.
Kissinger mnie kiedyś zachwycił pisząc, że polityka USA nie jest nigdy tak idealistyczna jak mówią jej chwalcy, ani tak egoistyczna, jak mówią krytycy. Czy jakoś podobnie 🙂
Tak serio, to te idee wpływają na życie, decyzje i czyny. Wpływają — wszędzie napotykają na opór, przede wszystkim konserwatystów zainteresowanych zachowaniem status quo, różnych zwolenników nagiej siły, chwalców wschodnich satrapii itp. itd. (Ten stary spór: kulturalne Ateny, czy brutalna Sparta*.) To co wychodzi to jakaś wypadkowa. Ale gdzie bylibyśmy, gdyby nie ten wpływ? Zwłaszcza, że w dłuższej perspektywie wygląda on na przemożny. Dzisiejsze status quo wygląda jak nierealne marzenia utopijnych lewaków sprzed dwustu lat.
—
*) Wiem, że to bardziej złożone, bo Ateny potrafiły być imperialistyczne i narzucać swoją władzę słabszym. Ale, mimo wszystko, Ateny są blisko wyobrażeniom dzisiejszych Stanów, ze względną równością, z kwitnącą nauką i sztuką; gdy ta zmitologizowana Sparta twardych ludzi, nie pokazała się nigdy żadną „lepszości” – była równie brutalnie imperialistyczna, wcale nie bardziej skuteczna w boju, a po swoim upadku nie zostawiła żadnego realnego dziedzictwa.
@PAK4
24 czerwca 2022
8:16
„@eche:
> Umhmm…A jakiej wypasionej bryki było to okienko?
Wiejskiego domu teściów, na pół-głębokiej prowincji. ‚
Czy serio masz tak grube okulary ideologii by tego nie widzieć?”
Ahaaa… wiejski dom teściów. To by było tak jakoś od 150000 do 350000 PLN (mediana). Fakt, równowartość bryki niezbyt wypasionej, ale na wypasioną czarną wołgę pewnie by starczyło. Ale na okulary z grubym szkłem już pewnie nie. A przydałyby się. Bo bez szkieł chyba nie widać z domku teściów walącego się właśnie systemu opieki zdrowotnej i zapadającego się systemu edukacji powszechnej, a nawet długu Polski nie w ruinie. I to mimo, że ten ostatni jest zaiste ogromny. Ruina nie jedno ma imię. BTW, jak tam u teściów idzie zbiórka chrustu do ocieplania domku z okienkem z pnienką?
aka.cia 24 CZERWCA 2022 0:44
Ten się śmieje, kto się śmieje ostatni…
PAK4 24 CZERWCA 2022 8:16 powtarzam za kolegą z blogu:
Thomas Piketty w „Time For Socialism”, rozdział „2018:The Year of Europe”, str. 165, zamieścił wykres pokazujący bilans przypływu i odpływu pieniędzy krajów Europy Środkowej – Polski, Węgier, Czech i Słowacji w latach 2010 – 2016. Dla każdego z nich był on ujemny, tj. odprowadzanie zysków z zachodnich inwestycji w produkcję i nieruchomości znacznie przekraczało dotacje Unii Europejskiej. Dla Polski w tym okresie odprowadzone zyski to 4,7% PKB, podczas gdy dotacje to 2,7% PKB, czyli -2%. To i tak nieźle w porównaniu z Czechami (zyski 7,6%, dotacje 1,9%, -5,7).
Zełeński buduje Israel w Unii … Tak sobie myślę prywatnie … Żydzi czy Israelczycy będą spadochroniarzami …
kalvarya01
24 CZERWCA 2022
7:50
Ależ dlaczego nie? Skoro wierni dają na tacę (na zbytki), w czym problem?
Skoro nawet komuna z czerwonymi legitkami PZPR dała ok. 100 mld (cóż wobec 100 mld znaczą datki na tacę), w czym problem?
100 mld (Komisja Majątkowa) dziś to ok. biliona…, a może więcej zważywszy na to, że majątek w najbardziej atrakcyjnych miejscach miast i wsi.
Dostają (nawet od komuny), to wydają, przejadają… Banał. Nawet liberał Tusk sypał na tacę (ślub kościelny przed wyborami). Banał.
PAK4
24 CZERWCA 2022
9:34
Ten przykład Aten i USA zachwycił mnie, zwłaszcza że nauka i sztuka kwitła w najlepsze sponsorowana przez niewolników.
Ilu niewolników mieli szlachetni moraliści Platon, Sokrates?
Media nad Wisłą sprowadzają konflikt na banderowskiej Ukrainie do wynoszenia muszli i pralek przez Rosjan … Tak sobie myślę prywatnie … czy w ramach Mińska nie mógł Zełeński zarządzić wystawkę … aby nie zadeptać dywanów …
PAK4
24 CZERWCA 2022
9:34
Dochodzimy do pewnych wniosków jak widzę…
1- Kissinger jest jednym z najbłyskotliwszych umysłów tej epoki.
I jest brutalnie szczery w swych wypowiedziach.
Cenimy go za to.
Warto zresztą znać WSZYSTKIE jego diagnozy.
Fakt, że prawie co roku odwiedza Putina, też o czymś świadczy.
2-Ateny wpadły w pychę, upoiły się swą mocarstwowością.
Sparta sprowadziła ich na ziemię, przeciwstawiając się despotyzmowi.
Dokładnie to obserwujemy w obecnej konfrontacji wschodu z zachodem.
Zwróciłbym też uwagę na język jakim posługują się Anglosasi i Rosjanie w swych publicznych wypowiedziach.
Takiego chamstwa, bezczelności, arogancji, buty, nie było na przestrzeni wieków.
Blinken, Sullivan, Johnson, ustanowili nowe standardy dyplomacji.
Żenujący poziom….
Pytanie do katolików nad Wisłą: Za ukrzyżowanie Jezusa odpowiada Israel czy Żydzi … a za Katyń Gruzini czy Rosjanie pod butem Gruzina … Tak sobie myślę prywatnie … żeby czarne było czarne …
PAK4 24 CZERWCA 2022 9:34
1. To są wszytko osiągniecia socjalistów z okresu, kiedy byli oni jeszcze marksistami, a które obecnie są odbierane ludziom pracy na tzw. Zachodzie. To nie burżuazyjni idealiści je wywalczyli, ale pracownicy najemni, poprzez strajki i inne pozaparlamentarne metody walki.
2. Czyny zawsze przeczyły słowom elit władzy na tzw. Zachodzie. Poza tym, to NIE idee (nadbudowa) wpływają na życie, decyzje i czyny (bazę), ale baza, czyli życie, decyzje i czyny kształtują ideologię, czyli nadbudowę. Napisał to już dawno temu pewien zachodnioniemiecki Żyd, a więc każdy, kto ma inne zdanie, jest z definicji antysemitą i rasistą. Pisała tez o tym też pewna polska Żydówka, także feministka, a więc na dodatek oskarżam cię też o antyfeminizm, zgodnie z obwiązującą dziś na tzw. Zachodnie Polityczną Poprawnością. ;-)
3. Ateny były tak samo niekulturalne jak Sparta, gdyż oba te państewka oparte były na niewolnictwie, ale Sparta zostawiła po sobie przynajmniej „ducha” walki, zdrowia psychicznego i fizycznego oraz oszczędności.
4. W USA nie ma równości – kwitną w niej tylko nauki „pracujące” na rzecz wojska i pseudo-sztuka popularna dla mas na poziomie czternastolatków. :-(
Szalom!
Herstoryk.
Ślązak- Czarna księga prywatyzacji.
Hongbing- Wojna o pieniądz
Perkins- Hitman ekonomista od brudnej roboty
Cukiernik- Dziesięć lat w UE bilans.
Warto przeczytać, ale plebs zapatrzony w przekaz TV nie ma na to ani czasu ani ochoty. Nie mówiąc już o inteligencji pozwalającej zrozumieć.
Propaganda sukcesu działa.
ontario 24 CZERWCA 2022 10:27
Tak, dają, bowiem zwyczajni ludzie są zwyczajnie głupi i w związku z tym dają się łatwo sobą manipulować elitom władzy via mass media. To jest też dowód na to, że demokracja jest wciąż niemożliwym do praktycznej implementacji ideałem, tak samo jak komunizm. A Tusk jest 100% hipokrytą, typowym zachodnim liberałem.
wiesiek59,
hmm…i nawet zadnego przykladu rosyjskiego dyplomaty nie dasz?! – (moze byc za a nawet przeciw).
Bias, czy ki czort…?
SŁOWIANIN STANISŁAW 24 CZERWCA 2022 10:47
Za ukrzyżowanie Jezusa odpowiada Chazaria, czyli dzisiejsza Ukraina.
re: 10:45 bylo
act 24 CZERWCA 2022 10:57
Tow. Mołotow!
Najpierw rozważmy gospodarkę Rosji. Publikacje, które mówią, że rosyjska gospodarka jest wielkości Teksasu, Belgii, Luksemburga czy czegokolwiek, po prostu przeliczają ruble na dolary i galopują do z góry ustalonego wniosku. Nigdy nie pytają, jak duży jest program kosmiczny kraju, do którego jest porównywana Rosja, ile produkuje atomowych okrętów podwodnych, czy otwiera nowe stacje metra, lotniska, mosty, czy ten kraj produkuje wszelkiego rodzaju samoloty i ciężarówki, albo jak dużo żywności, którą uprawia i eksportuje, czy cokolwiek innego, co faktycznie mierzy realną gospodarkę.
Oczywiście, gdy tylko to zrobią, zobaczą, że rosyjska gospodarka jest znacznie większa, niż sugeruje to dziecinne porównanie rubel-dolar. A nieco bliższe spojrzenie ujawniłoby, że rosyjska gospodarka jest prawie samowystarczalna. Ale Zachód nadal jest przekonany, że Rosja jest „stacją benzynową z bronią nuklearną”, a jej słabą gospodarkę można łatwo załamać. RAND oparł całą strategię na „ Największą słabością Rosji… jest jej gospodarka, która jest stosunkowo mała i wysoce zależna od eksportu energii
https://www.moonofalabama.org/2022/06/two-big-errors-about-russia-by-helmholtz-smith.html#comments
============
Na podstawie głupców o dochodach powyżej 200 000 rocznie, zatrudnionych w RAND co. podjęto idiotyczne decyzje.
„Sam tego chciałeś Grzegorzu Dyndało”…..
act
24 CZERWCA 2022
10:57
Klasa rosyjskich dyplomatów jest w porównaniu z anglosaskimi w stratosferze kultury, logiki, wiedzy, poziomu.
Nieosiągalna dla hołoty…
wiesiek59, 11:08,
to dlaczego piszesz:
‚Zwróciłbym też uwagę na język jakim posługują się Anglosasi i Rosjanie w swych publicznych wypowiedziach.’ – czyzby Freudian slip of tongue?
PS.
Dla Polski w tym okresie odprowadzone zyski to 4,7% PKB, podczas gdy dotacje to 2,7% PKB, czyli -2%. To i tak nieźle w porównaniu z Czechami (zyski 7,6%, dotacje 1,9%, -5,7).
Dla dokonania sprawiedliwej oceny należy też przyjrzeć się sumom włożonym przez zachodnich inwestorów w eks-komunistyczne przedsiębiorstwa, w porównaniu z zyskami. Inwestycje muszą przynosić jakiś zysk, kwestią jest jego proporcja do wkładu. Jeśli np. zapłacili grosze za działający koncern, dołożyli grosze na kosmetykę z marketingiem i ciągną nieproporcjonalne zyski unikając podatków, to albo natrafili na głupców albo na przekupnych.
Było by dobrze przeczytać to z uwaga i skupieniem bo troche to skomplikowane .. no ale co tam ..
( granice skomplikowania są nieokreślone i łatwo naruszalne przez czytających )
……………..
„Granice państw muszą być jasno określone i nienaruszalne.
Są jednak liczne odstępstwa od tej zasady co wielokrotnie tu przypominano, więc nikt nie jest bez winy, a zatem należy pomyśleć zanim rzucimy kamieniem ”
………………
„Coś musiało być na rzeczy skoro Rosjanie upomnieli się o swoje. ”
………………..
Co było ich na Ukrainie to wszystko jedno , bo tam „wszystko ” w ich mniemaniu było ich to i korupcja na pewno ( na czele z korupcja )
Co rosyjskiego jest na rzeczy w Polsce o co mogli by się Rosjanie upomnieć , a
w mniemaniu autora tych błyskotliwych myśli nikt nie jest .. eee .. każdy jest winien , ze ma cos rosyjskiego ale póki co jeszcze nie wie co to jest ?
Sadzac po wspomnieniach tych którzy mieli w……we szczęście ich spotkać wcześniej , nie rzucali kamieniami bo czuli się winni , ze w swoich walizkach mieli rosyjskie – gacie , skarpetki , koszule i i dwa krawaty i cos tam.
Tamci wcześniejsi Rosjanie nie wiedzieli w której tnp te krawaty są , wiec zabrali wszystkie tnww . Kilkanaście ich było dlatego potrzebna była ” furmanka ” i dwie pepesze aby dać rade się upomnieć .
Były na furmance dlatego była ona rzeczą na której były te walizki .. już rosyjska w tym czasie bo odzyskana , a ziemie okoliczne tez były świeżo rosyjskie a i Odzyskane
Jest od pewnego czasu sporo tekstów na temat Pułapki Tukidydesa.
Stare mocarstwo zdycha pod ciosami nowego.
Ale, usiłuje bronić stanu posiadania za wszelką cenę.
Poświęcając wszystkich wiernych wasali by przedłużyć agonię.
Stare elity nie chcą stracić władzy, pozycji, majątku.
Kto powiedział, że Afryka nie może kupić zboża … Taki sobie myślę prywatnie … wystarczy ogłosić zbiorowy zakup pod auspicjami np. ONZ …
kalvarya01
24 CZERWCA 2022
10:56
Nie są głupi. Wiedzą, gdzie żyją i co od kogo zależy. Mądrością przodków, własnym rozsądkiem próbują ocalić siebie, swe rodziny, swe znikome na ogół dobra, kawałek ziemi, łąkę, dawniej lepiankę, dziś domek zbudowany na kredyt, który z odsetkami spłaca się przez 30 lat, ale najpierw trzeba spłacić odsetki.
Co do Tuska, nie ma złudzeń. Wysoko siadł, wysoko wyszedł ze swoich nizin, trudno byłoby mu spaść, trzeba kombinować co tchu.
wiesiek59
24 CZERWCA 2022
10:50
Plebs nie ma czasu ani sił, aby się zapatrzeć w TV. Plebs tyra od świtu do nocy, aby zbudować dom na kredyt, kupić mieszkanie i wreszcie pozbyć się używanych aut, które Zachód sprzedał plebsowi za parę euro.
@Wiesiek59:
> rosyjska gospodarka jest wielkości Teksasu, Belgii, Luksemburga czy czegokolwiek, po prostu przeliczają ruble na dolary i galopują do z góry ustalonego wniosku. Nigdy nie pytają, jak duży jest program kosmiczny kraju
Roskosmos głównie bierze udział w projektach międzynarodowych i pracuje nad rodziną rakiet (używane rakiety technologicznie są z lat 60-tych) — 3 testowe starty w ostatniej dekadzie.
> ile produkuje atomowych okrętów podwodnych
Muszę powiedzieć, że się zdziwiłem — w ostatniej dekadzie Rosja zwodowała jeden atomowy okręt podwodny. Luksemburg nie buduje. USA zwodowały w tym czasie 9 sztuk — że Teksas to ok. 10% PKB USA, więc mniej więcej to jest ten poziom.
> lotniska
No właśnie, brak baz wojskowych jest jedną z przyczyn słabej obecności rosyjskiego lotnictwa w wojnie w Ukrainie.
> wszelkiego rodzaju samoloty
Jeszcze tak.
Tyle, że Rosja nie produkuje awioniki do dużej części swoich konstrukcji, więc jest pytanie, czy będzie mogła je nadal produkować.
> ciężarówki
Ciężarówki — może. Za to z osobówkami ma problemy — podobno (powołuję się na Izwiestię) stanęły wszystkie fabryki samochodów osobowych w Rosji. Powód: brak odpowiedniej stali i innych importowanych komponentów.
„Stare elity nie chcą stracić władzy, pozycji, majątku. ” …
….. sugeruje , ze są już nowe gotowe odzyskiwać władze , pozycje i majątek .
Powinny zdać sobie sprawę , ze w momencie odzyskania staną się starymi i powinny mieć się na baczności od początku .
„Wedle Paula Johnsona , jednym z największych grzechowe intelektualistów , jest ich wiara w możliwość zmiany świata i stosowanie inżynierii społecznej ”
ale blogowianie tutejsi mogą spać spokojnie bo tutaj ich nie ma .
5 etapów upadku społeczeństwa Dimitriego Orłowa (2008 i wielokrotnie poprawiane od tego czasu)
http://cluborlov.blogspot.com/2008/02/five-stages-of-collapse.html?m=1
olborski
24 CZERWCA 2022
12:06
To stary, odwieczny cykl.
Król umarł, niech zyje król!!!
Pierwsze skrzypce grały elity niemieckie, francuskie, hiszpańskie, austiackie, brytyjskie- jeżeli chodzi o Europę.
W swoje krajowe zasoby.
Konflikty pomiędzy konkurentami trwały po kilkadziesiąt lat.
Wojna XXX letnia o prymat w Niemczech- na przykład.
Czy Wojna Stuletnia, trwająca 120 lat pomiędzy Francją a Anglią.
Polki konflikt z Rosją i Turcją miał chyba ponad 200 lat.
Przegraliśmy.
A Turcja została zdradzona przez dawnych sojuszników i rozparcelowana.
„Brytania nie ma wiecznych przyjaciół ani wrogów, wieczne są tylko jej INTERESY”…
ELIT europejskich czy amerykanskich nie zastapią rosyjskie czy chińskie.
Z prostego powodu.
Mają inne priorytety.
„Pełne spektrum dominacji” roi sie w głowach jedynie Anglosasom.
Chinom, Indiom czy Rosji, jedynie spokojny handel na własnych warunkach.
Partnerstwo, nie wasalizowanie.
Cenzura jest nielegalna (Konstytucja: „Każdemu zapewnia się wolność wyrażania swoich poglądów oraz pozyskiwania i rozpowszechniania informacji”).
Tę wolność łamią w Polsce na każdym kroku, co szczególnie jaskrawo widać u tych, którzy wołają „Kon-sty-tu-cja!”, a nawet na koszulkach przybitych do własnych tułowi piszą „KONSTYTUCJA”.
2. Mają (np. „Polityka”) listę nicków, które z automatu, bez czytania tekstów osób określonych tymi nickami, są cenzurowane i odrzucane:
„Nie, nie wszystkie wpisy są czytane przed publikacją, bo niektóre pseudonimy autorów od razu sugerują, że ich wpisy do publikacji na tym forum się nie kwalifikują”. (Adam Szostkiewicz 23 CZERWCA 2022 9:11″.
Istnieje zatem indeks nicków, automat unicestwia każdy wpis bez czytania. Oto i wolność wypowiedzi w Polsce.
@ontario:
Nie myślałem, że mam konstytucyjne prawo włączyć się w linię komunikacji straży pożarnej i nadawać tam 24/7 swoje poglądy. Dzięki — zmieniłeś moje cele życiowe 😛
PAK4
24 CZERWCA 2022
12:42
Nie pomyliłem się w swoich domniemaniach: nie znasz Konstytucji własnego kraju.
Natomiast serdecznie dziękuję za to, że mnie, czyli ontario, utożsamiasz z Konstytucją, jej zapisem o wolności wypowiedzi.
https://www.youtube.com/watch?v=G11HqBqtkj8
==========
Pułkownik Baud w niedostępnej niestety dla mnie wersji mówionej.
wiesiek59 24 CZERWCA 2022 11:03
Wyślij to PAK-owi #4:
GDP (PPP, US$ million)
Kraj IMF(MFW) Rok Bank Światowy Rok CIA Rok
Chiny 30,177,926 2022 24,273,360 2020 23,009,780 2020
USA 25,346,805 2022 20,936,600 2020 19,846,720 2020
UE 23,730,275 2022 20,046,175 2020 19,885,625 2019
India 11,745,260 2022 9,907,028 2020 8,443,360 2020
ASEAN 10,131,237 2022 8,238,168 2020 7,826,781 2020
Japonia 6,110,075 2022 5,328,033 2019 5,224,850 2019
Niemcy 5,269,963 2022 4,469,546 2020 4,238,800 2020
EAEU 5,242,218 2022 4,896,309 2020 4,606,458 2019
Rosja 4,365,443 2022 4,133,084 2020 3,875,690 2020
Indonezja 3,995,064 2022 3,302,377 2020 3,130,470 2020
UK (GB) 3,751,845 2022 3,019,057 2020 2,797,980 2020
Brazylia 3,680,942 2022 3,153,597 2020 2,989,430 2020
The Eurasian Economic Union (EAEU or EEU) czyli Euroazjatycka Unia Gospodarcza, EUG (ros. Евразийский экономический союз, biał. Еўразійскі эканамічны саюз, kaz. Еуразиялық экономикалық одақ, orm. Եվրասիական տնտեսական միություն, kir. Евразиялык экономикалык биримдик, ang. Eurasian Economic Union, EAEU) jest to unia gospodarcza powołana 29 maja 2014 przez trzy państwa założycielskie: Białoruś, Republikę Kazachstanu i Federację Rosyjską. Do unii dołączyły także Armenia (10 października 2014 roku) oraz Kirgistan (23 grudnia 2014 roku). Traktat powołujący do życia Unię przewiduje poszerzenie dotychczasowej unii celnej o swobodny przepływ kapitału, siły roboczej, towarów i usług. Unia ta jest w publicystyce często określana jako alternatywa dla Unii Europejskiej.
PAK4 24 CZERWCA 2022 12:42
Jeśli jesteś Komendantem Straży Pożarnej w swojej gminie, to kto ci tego zabroni?
@ontario:
Wiesz, dzięki głosom takim jak Twój, ja się tu czuję orłem szybującym ponad otchłanią intelektu internetowych trolli. No i przechodzę w tryb szyderstwa.
Wolność słowa, nie oznacza, że wszędzie wszystko wolno mówić. Są miejsca, gdzie to gospodarz miejsca zaprasza, daje i odbiera głos. Nie idziesz przecież do telewizji i na bramkach nie mówisz, ja, ontario, mam przesłanie do narodu polskiego!, które to zdanie otwiera wszystkie drzwi i pozwala ci nadawać na cały kraj. Albo inny przykład — mieliśmy serię protestów w kościołach przeciwko pedofilii, czy zaostrzenia ustawy prawa antyaborcyjnego. Sąd orzekał winę, za zakłócanie mszy świętej. A przecież konstytucyjna wolność wypowiedzi.
Oczywiście, gdy mówię o komunikacji straży pożarnej, to przechodzę w tryb szydery i pokazuję absolutną skrajność. To nawet do osłów powinno dotrzeć, że prawo zapisane w konstytucji tego nie dotyczy. No, ale widać jak dociera.
@ontario 24 CZERWCA 2022 12:33 oraz
@PAK ogólnie:
W realnym kapitalizmie rynkowym z definicji istnieje tylko jedna realna wolność – wolność robienia interesów dla garstki najbogatszych.
„Amerykanie są w kłopocie. Do wszystkich części świata, znajdujących się pod ich wpływem, eksportują broń, amunicję, papierosy, oficerów sztabowych i konserwy, ale zdają sobie sprawę z tego, że to za mało. Chcieliby eksportować jakąś ideologię, made in USA, w dobrym gatunku, przystępną, solidnie zrobioną, która raz na zawsze przekona Greków, Francuzów czy Włochów, że muszą walczyć, a gdyby do tego przyszło, i umierać za amerykański styl życia. Potrzeba ideologii jest paląca, ale na razie Amerykanie posiadają na składzie tylko jedno hasło, które nie bardzo starczy na doktrynę; to kwiat wolności amerykańskiej, najwyższa swoboda, „freedom of enterprise” czyli wolność robienia interesów” – Stanisław Lem „Widmo trzeciej wojny w USA” Nowa Kultura (nr 51-52 z roku 1952). Lem przypomniał też w tym artykule, że: „Pewien doskonały specjalista, profesor chemii, Spitzer, stracił katedrę, gdy z ośmielił się powiedzieć, że być może, Łysenko ma w swojej teorii biologicznej trochę racji. Por. William de Jong-Lambert “The ‘Spitzer Affair’: Genetics, McCarthyism and the Cold War” w Jarosław Suchoples i Katy Turton (red.) “Forgotten by History: New Research on Twentieth Century Europe and America” Berlin: LIT Verlag, 2009 str. 71–85. Należy tu zauważyć, że Spitzera poparł także dwukrotny noblista, amerykański biochemik Linus Pauling w tym sensie, że Spitzer został ocenzurowany i był prześladowany przez amerykańskie władze dokładnie w ten sam sposób, w jaki radzieckie (jak kto woli rusycyzmy, to sowieckie) władze cenzurowały i prześladowały wówczas przeciwników Akademika Łysenki.
dla tych co maja wątpliwości .. rzucać kamieniem czy nie aby kosa na niego trafiła ( nie czują się winni ale nie wiedza co czują , nie sa pewni)
(„Coś musiało być na rzeczy skoro Rosjanie upomnieli się o swoje. ” )
https://www.youtube.com/watch?v=L4jYV0oH65E
PAK4 24 CZERWCA 2022 13:17
Do tej pory nie wiedziałem, ale teraz dzięki tobie wiem, że możesz się czuć orłem, a nie sobą…
Twój przykład telewizji jest idealnej jakości, ponieważ nawet gdyby mi dopłacali, nawet gdyby mnie prosili, abym całą dobę nadawał na cały kraj, to i tak bym się wypiął na telewizję.
To samo z kościołem a nawet przed kościołem.
Epitet osioł to dla mnie komplement. Nawet do takich jak ty, którzy się czuje orłem, to nie dotrze, że twoje szyderstwo to dla mnie pieszczota.
kalvarya01
24 CZERWCA 2022
13:25
Doskonałe interesy na swoje możliwości każdego dnia robi każdy rodak/Polak, gdy tylko chce.
Nawet ci, którzy z zasady nie kiwną palcem, także robią doskonałe interesy. Państwo bowiem za to nic nie robienie daje im każdego miesiąca sporą gotówkę, którą obracają na raczenie się piwem w cieniu publicznego parku.
Niektórzy to nawet dostają dopłaty od kapitalistów, aby nie siali, nie orali pól, a jeśli zasieją, to żeby nie zbierali plonu.
PAK4 24 CZERWCA 2022 13:17
Jesteś jak ptak dodo, czyli nielotem. ;-)
Dront dodo (Raphus cucullatus) – wymarły gatunek dużego ptaka z rodziny gołębiowatych (Columbidae), podrodziny treronów (Raphinae). Występował endemicznie na wyspie Mauritius. Najprawdopodobniej ostatnie ptaki tego gatunku zabito w roku 1662. Choć to właśnie dodo jest najczęściej wspominanym wymarłym gatunkiem, niemal nic nie wiadomo o życiu tych ptaków na wolności.
Poza tym, to raz piszesz, że wolność słowa, nie oznacza, że wszędzie wszystko wolno mówić a innym razem popierasz @aka.cia w jego chamskich atak na mnie. A jeśli PanBóg pozwolił na zakłócanie owej „świętej myszy”, to znaczy, że jest Mu to miłe, tak jak np. tu:
1 Pan wezwał Mojżesza i tak powiedział do niego z Namiotu Spotkania1: 2 Mów do Izraelitów i powiedz im: Jeśli kto z was zechce złożyć dar z bydląt dla Pana, niech złoży go albo z cielców, albo z mniejszego bydła.
Ofiara z cielców
3 Jeżeli chce złożyć na ofiarę całopalną dar z bydła, niech weźmie samca bez skazy i przyprowadzi go przed wejście do Namiotu Spotkania, aby Pan przyjął go łaskawie. 4 Położy rękę na głowie żertwy, aby była przyjęta jako przebłaganie za niego. 5 Potem zabije młodego cielca przed Panem, a kapłani, synowie Aarona, ofiarują krew, to jest pokropią nią dokoła ołtarz stojący przed wejściem do Namiotu Spotkania. 6 Następnie obedrze żertwę ze skóry i podzieli ją na części. 7 Kapłani, synowie Aarona2, przyniosą ogień na ołtarz i ułożą drwa na ogniu. 8 Potem kapłani, synowie Aarona, ułożą części wraz z głową i tłuszczem na drwach leżących na ogniu na ołtarzu. 9 Wnętrzności i nogi zwierzęcia będą obmyte wodą. Kapłan zamieni to wszystko w dym na ołtarzu. To jest całopalenie, ofiara spalana, miła woń dla Pana.
Ofiara z baranków i koziołków
10 Jeżeli zaś kto chce złożyć na ofiarę całopalną dar z trzody, z baranków lub koziołków, niech weźmie samca bez skazy. 11 Będzie on zabity po północnej stronie ołtarza, przed Panem, a kapłani, synowie Aarona, pokropią krwią Jego ołtarz dokoła. 12 Potem podzielą go na części. Kapłan ułoży je wraz z głową i tłuszczem na drwach leżących na ogniu, na ołtarzu. 13 Wnętrzności i nogi zwierzęcia będą obmyte wodą. Kapłan złoży w ofierze to wszystko i zamieni w dym na ołtarzu. To jest całopalenie, ofiara spalana, miła woń dla Pana.
Ofiara z gołębi
14 A jeżeli kto chce złożyć w darze ptaka jako całopalenie dla Pana, niech złoży w darze synogarlicę lub młodego gołębia. 15 Kapłan przyniesie go do ołtarza, złamie mu główkę i zamieni go w dym na ołtarzu. Krew jego wyciśnie na ścianę ołtarza. 16 Potem oddzieli wole jego wraz z piórami i wyrzuci je na popielisko, na wschód od ołtarza. 17 Następnie kapłan naderwie jego skrzydła, jednak nie oddzielając ich całkowicie, i zamieni w dym na ołtarzu, na drwach leżących na ogniu. To jest całopalenie, ofiara spalana, miła woń dla Pana.
Księga Kapłańska 1
Takoż:
Noe zbudował ołtarz dla Pana i wziąwszy ze wszystkich zwierząt czystych i z ptaków czystych, złożył je w ofierze całopalnej na tym ołtarzu. Gdy Pan poczuł miłą woń, rzekł do siebie: ‘Nie będę już więcej złorzeczył ziemi ze względu na ludzi, bo usposobienie człowieka jest złe już od młodości.
Przeto już nigdy nie zgładzę wszystkiego, co żyje, jak to uczyniłem. Będą zatem istniały, jak długo trwać będzie ziemia: siew i żniwo, mróz i upał, lato i zima, dzień i noc’.
Księga Rodzaju 8
Poza tym, to twoje poczucie humoru jest, jakby tu powiedzieć, bawarskie w tym sensie, że szczytem wyrafinowania jest u ciebie wzajemne kopanie sie po dupach i okładanie po mordach (pardon, citoyens de la ville de Mordy).
Szalom!
kalvarya01
24 CZERWCA 2022
13:25
Otóż, panie orle, ja, osioł (także patentowany) mam przyjemność ci wyryczeć, że Konstytucja mówi o wolności słowa i o tym pisałem. Natomiast Konstytucja nie mówi, gdzie ta wolność może zaistnieć i dlatego o tym nie pisałem.
Twój szyderczy i genialny tekst nie dotyczy zatem tego, o czym pisałem, jest o twoich urojeniach na mój temat.
Ale nawet twoje urojenia i twoje szyderstwo mile mnie łechczą.
ontario 24 CZERWCA 2022 13:36
Albowiem powiadam Ci: „Spójrzcie na te ptaki niebieskie, że nie sieją ani żną, ani zbierają do gumien, a Ojciec wasz niebieski żywi je: (Mat. 6:26).
ontario 24 CZERWCA 2022 13:42
Miłego łechtania łechtaczek. 😉 Niekoniecznie muszą być koszer. 😉
PAK4 napisal ‚glosom’ @ontario przeczytal ‚oslom’? Dziwne
PAK4 24 CZERWCA 2022 11:58
@PKB USA: Ponad 80% PKB w tzw. krajach rozwiniętych stanowią usługi, a wiele z nich jest de facto bezwartościowych poza nimi (np. usługi świadczone w USA przez amerykańskich prawników, księgowych, maklerów giełdowych, doradców podatkowych itp.) Dlatego też PKB USA wydaje się być mocno zawyżony.
Ponadto w ostatniej dekadzie XX wieku wiele krajów zachodnich, a zwłaszcza USA, wprowadziło nową metodologię obliczania PKB, która jest niezgodna z metodami stosowanymi w pozostałych krajach świata. Polega ona na sztucznym zawyżaniu wartości niektórych dóbr, głównie tzw. wysokiej techniki (lub zaawansowanej technologii – po angielsku high tech), takich jak komputery i ich oprogramowanie, których ceny mnoży się przez arbitralnie ustalone przeliczniki (mnożniki), aby zrekompensować spadek ich cen, związany z postępem technicznym, a także na dodawaniu do PKB hipotetycznych czynszów, „zarabianych” przez ludzi mieszkających we własnych mieszkaniach (tzw. czynsze kalkulacyjne, po angielsku imputed rents). Nie chodzi tu głównie o poprawność tej metodologii, ale raczej o fakt, że nie każdy kraj stosuje te arbitralnie przyjęte mnożniki i uwzględnia fikcyjne dochody z nieistniejących czynszów, przez co PKB takich krajów (np. USA) jest sztucznie i arbitralnie zawyżany w stosunku do innych krajów, które nie stosują tych mnożników i nie dodają do PKB fikcyjnych dochodów z czynszów. Oficjalna nazwa tej metody to „Hedonic Methods for Quality Adjustment” („Hedoniczne metody korekty jakości” – patrz np. Stewart, K.J. & Reed, S. „Consumer Price Index research series using current methods” w „Monthly Labor Review”, czerwiec 1999).
Ponadto – według ONZ – PKB oznacza jedynie produkcję tych dóbr i usług, które są sprzedawane na rynku. Wśród tych dóbr i usług są nie tylko te, które poprawiają dobrobyt i dobrostan ludności danego kraju, ale także te, które ten dobrobyt i dobrostan po prostu zmniejszają. PKB mierzy też usługi rządowe po kosztach (a więc je zaniża) i nie obejmuje tej części produkcji rolnej, która pozostaje w gospodarstwie (co zaniża PKB mniej rozwiniętych państw) i nie obejmuje produkcji gospodarstw domowych, zwłaszcza produkowanej przez kobiety, ponieważ do PKB wlicza się tylko to, co jest sprzedawane, a w praktyce to przecież nie jest wszystko. PKB jest więc seksistowski, ale „genderowcy” tacy jak np. @PAK4 po prostu NIE chcą tego zauważyć.
Produkcja sektora nieformalnego, spora szczególnie w krajach mniej rozwiniętych też nie jest (na ogół) w ogóle wliczana do PKB – rasistowska dyskryminacja tzw. III świata. Ogólne dane na temat całkowitego PKB i jego średniej czyli „na głowę mieszkańca” nie dostarczają też żadnych informacji na temat podziału dochodów i korzyści ekonomicznych dla różnych grup społecznych, które mogą one uzyskać w wyniku rozwoju gospodarczego. PKB nie mówi też nic o warunkach pracy i satysfakcji z niej czerpanej; nie mówi też nic o poziomie uczestnictwa w życiu narodowym różnych grup społecznych i nie mówi nic o innych ważnych wymiarach rozwoju, takich jak sytuacja demograficzna i warunki polityczne.
Porównania międzynarodowe często zawodzą także ze względu na fakt, że kursy walutowe nie nadają się do określania względnej siły nabywczej walut, zwłaszcza w dziedzinie konsumpcji dóbr i usług przez gospodarstwa domowe. Badania alternatywnych metod porównywania PKB między krajami, opartych na sile nabywczej walut, wskazują, że konwencjonalne przeliczanie walut (czyli według kursu wymiany) może wyolbrzymiać względny dystans ekonomiczny między krajami o wysokim i niskim PKB na mieszkańca (per capita). Dobrze ilustruje to fakt, że nikt nie mógłby przeżyć w krajach wysoko rozwiniętych („uprzemysłowionych”) z dochodu ocenianego jako całkowicie wystarczający do przeżycia w krajach biedniejszych („rozwijających się”), podobnie jak absurdem jest przeliczanie PKB PRL-u przy użyciu spekulacyjnego, czarnorynkowego kursu dolara USA względem złotówki.
Patrz: United Nations (ONZ) „Overall Socio-economic Perspective of the World Economy to the Year 2000” – „Ogólna perspektywa społeczno-gospodarcza gospodarki światowej do roku 2000” Nowy Jork: ONZ, 1990.
@kalvarya01:
Jest piątek, jestem zmęczony, nie bawią mnie dzisiaj chińskie uprzejmości, z prawieniem przewrotnych komplementów, w których ukryty jest jad. Jeśli z moich żartów rozumiesz tylko kopanie po dupach to mnie nie dziwi — w końcu najlepiej poznać dowcip na własnym poziomie. Sorry, ale ja to dobrze znam — ten typ, który wciąż woła o wolność słowa by kłamać, manipulować, wyzywać innych, ale sam przy pierwszym przytyku biegnie po prokuraturę i domaga się cenzury.
ontario 24 CZERWCA 2022 11:46
Jeśli by byli mądrzy, to nie dawali by się wyzyskiwać garstce cwaniaków bez moralnych skrupułów.
PAK4 24 CZERWCA 2022 13:51
To NIE jest „przytyk”, to jest zniesławienie, czyli przestępstwo karane na podstawie kodeksu karnego.
kalvarya01
24 CZERWCA 2022
13:46
Wolę, gdy łechtaczki łechczą mnie.
kalvarya01
24 CZERWCA 2022
13:44
Zaiste, nie wiedziałem, że Ojciec jest kapitalistą. Dziękuję za zbędną dla mnie informację.
act
24 CZERWCA 2022
13:47
Napisał „osłów”, co mi sprawia przyjemność: „To nawet do osłów powinno dotrzeć…”.
PAK4
24 CZERWCA 2022
13:51
PAK4 zna mnie i podaje przykłady moich kłamstw, manipulacji, wyzywania innych i mojego biegania do prokuratorów. To są niezbite dowody, uwierzcie PAK4. Tak, kłamię, manipuluję, wyzywam innych (wystarczy przejrzeć moje wpisy) i biegam do prokuratorów.
kalvarya01
24 CZERWCA 2022
13:53
Są mądrzy, dlatego pozwalają wierzyć cwaniakom, że zostali przez nich wykiwani bez moralnych ograniczeń.
Coś o BRICS
BRICS oznacza Brazylię, Rosję, Indie, Chiny i Republikę Południowej Afryki. Brazylia reprezentuje Amerykę Południową, od Meksyku po Argentynę i Karaiby. Rosja reprezentuje Europejczyków, którzy są normalni i ludzcy, w tym przywódców takich jak Łukaszenka z Białorusi, Orban z Węgier, Vlasic z Serbii i im podobnych. Indie i Chiny reprezentują całą Azję, a Afryka Południowa – Afrykę.
Kogo zaś pominięto? A zbrodniczych imperialistów, na czele z USA, oraz marionetkowe rządy w Europie. To jest mniej niż 80% światowej populacji i rynku.
Rosja jest zdecydowanie największym krajem na świecie pod względem terytorium i naturalnie najbogatszym w zasoby naturalne. Posiada wszystkie bogactwa naturalne, od niezmierzonych terenów rolniczych, które mogą wyżywić cały świat, w nieskończoność.
Rosja i Rosjanie, do spolki z z Chinami, są darem dla świata, który ma go chronić przed złem. A tym obecnie jest kierowany przez USA Zachód.
Zachód brutalnie i bezlitośnie działa przeciwko Wschodowi i Południowowi, w tym przeciwko Rosji, Chinom, Indiom i innym pozostałym a ogromnym krajom tamtego rejonu globu, takim jak Pakistan, Bangladesz czy Indonezja.
Jest to zapowiedź rychłego, niszczycielskiego końca tak zwanego „Zachodu”.
(Przetłumaczono z http://www.DeepL.com/Translator (wersja darmowa) )
Czyli co? Całkowity doom and gloom dla nas?
Nic, tylko się pochlastać
Motyw sądów zasługuje na powieść-rzekę liczącą milion stron.
Warto bronić wolności sądów-trzeciej władzy, bo to od sądu zależy kwalifikacja czynu. Np. konstytucyjna wolność wypowiedzi może przegrać z mszą. Zresztą, sąd wykazał się trzeźwą znajomością realiów.
Dlatego też warto bronić, bo można mieć telefon np. do prezesa sądu, a ten już ustali, co pasuje telefonującemu.
Orteq
24 CZERWCA 2022
14:16
Eeeee, dlaczego od razu się chlastać, jest jeszcze Korwin-Mikke mający Putina za Ekscelencję.
ontario 14:05,
rzeczywiscie przegapilem, bom sam osiol.
Choc, kiedy sam sobie to powtarzam, nie biore tego zbyt osobiscie 🙂
@ontario
24 czerwca 2022
13:36
„Niektórzy to nawet dostają dopłaty od kapitalistów, aby nie siali, nie orali pól, a jeśli zasieją, to żeby nie zbierali plonu.”
Nie do końca tak – obsiać trzeba. Jest to kontrolowane przez inspektorów, a nawet przez satelity.
Sprytny ludek na pół-głebokiej prowincji ( byłem świadkiem; może małżonka PAK4 widziała to też przez okienko teściów i potwierdzi? ) radzi sobie w ten sposób, że obsiewa areał czymś nie wymagającym specjalnego zachodu, np koniczyną, nastyępnie kasuje dotacje z Junii i zapomina na pare miesięcy o uprawie. Po tej parze miesięcy zaś, wyjeżdża na pole traktorem z pługiem i zaoruje bylinę, przygotowując matkę ziemię pod przyszłoroczne zbiory dotacji. W przypadku macherów z większym areałem popularny był tez sposób na uprawę orzecha włoskiego (oczywiście z pominięciem zaorania).
Na czym polega siła nabywcza głównych walut swiatowych?
Na arbitralnym ustanowieniu kursów wymiany.
Jak oblicza się produktywność?
Bierze się walutę lokalną i przelicza na dolary.
Dokładnie takie same czynnosci, według tych samych metod pracy, narzędzi, dają absurdalne róznice.
Samochód złożony w Chinach, Polsce i Niemczech, jest dokładnie taki sam, ma taki sam wkład energii i pracy.
A jednak „produktywność” Chińczyka będzie 10 krotnie mniejsza niż Niemca.
Fantastyczne sa te absurdy w które każą nam wierzyć…
eche
24 CZERWCA 2022
14:31
Wszystko się gites zgadza.
Jednak nie użyłbym słowa „macherzy”. Plantacje orzecha włoskiego posadzonego na ugorach widziałem, oczywiście, orzechy wyschły, co było wiadome od początku, że na ugorze wyschną, ale skoro dają i płacą, widocznie kapitaliści wiedzą, co robią…
act
24 CZERWCA 2022
14:26
Mnie natomiast pieszczą słowa, którymi obdarzają mnie orły, bo wtedy uwidacznia się bezradność orła w starciu z osłem.
Orteq
24 CZERWCA 2022
14:16
Prawdopodobnie Kanada ma bardzo podobne zasoby mineralne, jako składnik tego samego prakontynentu.
Tyle że poświęciła mniej czasu i pieniędzy na badania geologiczne, budowę ciągów komunikacyjnych umozliwiających eksploatację.
Może to i sensowne, przyda się na zaś….
@wiesiek59:
> Na czym polega siła nabywcza głównych walut swiatowych?
Na arbitralnym ustanowieniu kursów wymiany.
Rynkowo. Czyli jest to cena umowna za wymianę. Czyli: jeśli nie chcesz kupować dolarów, czy euro, to proszę bardzo — nikt Cię nie zmusza, a czym więcej osób postąpi tak samo, tym niższy będzie ich kurs.
> Samochód złożony w Chinach, Polsce i Niemczech, jest dokładnie taki sam, ma taki sam wkład energii i pracy.
Niekoniecznie.
Wkład energii i pracy będzie zależał od wyposażenia linii produkcyjnej, kompetencji pracowników, czy sposobu zarządzania produkcją. Przy czym dwa ostatnie punkty zależą w pewnym stopniu od „kultury narodowej”.
@eche:
Raczej komasację gruntów. Wieś się starzeje, starsi rolnicy nie chcą wyprzedawać roli, więc oddają ją w dzierżawę nielicznym młodszym, którym się chce. Ci zaś kupują maszyny, inwestują i jakoś na tym wychodzą. Jak się dzielą przy tym dopłatami — nie wiem.
W każdym razie wzrost zamożności widać gołym okiem. Czy to względnie więcej warte w sile nabywczej emerytury, czy praca młodych na emigracji, czy poprawa efektywności gospodarowania na tak skomasowanych gruntach, przy dostępie do nowego sprzętu rolniczego (zachodniego) — widać, że wszystko to na raz, choć nie wiem w jakiej proporcji.
@kalvarya01:
> To NIE jest „przytyk”, to jest zniesławienie, czyli przestępstwo karane na podstawie kodeksu karnego.
Czyżby kodeks karny był niezgodny z konstytucją? (Hint: nie jest niezgodny. To Wy nie rozumiecie wolności słowa.)
Czyżbyś dokonał tu kilku zniesławień, choćby twierdząc, że uprawiam amerykańską propagandę za pieniądze, albo że popieram Tuska i moim ulubieńcem jest Joe Biden?
PAK4
24 CZERWCA 2022
14:59
Bzdury.
Światowym rynkiem finansowym rządzi kartel zachodnich banków prywatnych.
To samo z głównymi giełdami.
To dawało zarówno przewagę konkurencyjną jak i „darmowe obiadki” dla drukujących kasę bez pokrycia.
I mamy to co mamy.
Zachód jest od lat niewypłacalny, jedzie na deficycie handlowym i budżetowym.
Ale, sam sobie przyznał rating AAA.
Teraz czaka na sprawdzenie swych kart i mozliwości.
Blotki mogą wygrać w pokera, ale nie w brydża.
Toczy się zdecydowanie inna gra moim zdaniem,
W szachy, bądź GO.
A tu wymagane są całkiem inne predyspozycje.
Długofalowe planowanie, budowanie pozycji, nie blef.
wiesiek59
24 CZERWCA 2022
15:14
PAK4
24 CZERWCA 2022
14:59
Bzdury.
Światowym rynkiem finansowym rządzi kartel zachodnich banków prywatnych.
To samo z głównymi giełdami.
To dawało zarówno przewagę konkurencyjną jak i „darmowe obiadki” dla drukujących kasę bez pokrycia.
I mamy to co mamy.
Porozumienie z Plaza – umowa międzynarodowa pomiędzy przedstawicielami krajów ówczesnego G5 (Francji, Republiki Federalnej Niemiec, Japonii, Stanów Zjednoczonych i Wielkiej Brytanii), która została zawarta 22 września 1985 r. w hotelu Plaza w Nowym Jorku. W wyniku porozumienia uczestnicy zgodzili się na dewaluację dolara amerykańskiego względem jena i marki niemieckiej poprzez kontrolowane wywieranie wpływu na międzynarodowe rynki walutowe.
https://pl.wikipedia.org/wiki/Porozumienie_z_Plaza
==========
Tak się ustawia kursy walutowe.
To rynek, czy polityka?
Od czasu utworzenia Rezerwy Federalnej Stanów Zjednoczonych ponad sto lat temu, każde większe załamanie rynku finansowego było celowo powodowane przez bank centralny z motywów politycznych.
Nie inaczej jest dzisiaj, ponieważ najwyraźniej amerykański Fed działa ze swoją bronią stóp procentowych, aby rozbić największą bańkę spekulacyjną w historii ludzkości, bańkę, którą stworzył. Globalne krachy zawsze zaczynają się na peryferiach, tak jak porażka austriackiego Creditanstalt z 1931 r. czy Lehman Bros. we wrześniu 2008 r. Decyzja Fed z 15 czerwca o narzuceniu największej jednorazowej podwyżki stóp procentowych od prawie 30 lat, teraz gwarantuje globalną depresję gospodarczą.
https://polskawliczbach.blogspot.com/2022/06/planowane-na-caym-swiecie-finansowe.html
Oto czego Hartman nie puścił (nie moje):
Jeśli Pani Jachira byłaby realnym zagrożeniem dla interesów rządzących a właściwie ich mocodawców to by skończyła jak Gabriel Janowski albo nawet (czego absolutnie jej nie życzę !) jak Andrzej Lepper.
Niech wykaże się jakimiś realnymi działaniami – np. wyjdzie z propozycją konkretnej ustawy , pozyska dla niej poparcie polityków, posłów i senatorów, partii , organizacji społecznych i szerokich rzesz społeczeństwa.
A tak to tylko taka pacynka „na pokaz” – jak to się mawia – „mocna tylko w gębie” w efekcie działająca tylko na korzyść aktualnie rządzących.
ontario 24 CZERWCA 2022 14:09
Gdyby byli mądrzy, to by nie żyli w biedzie, tak jak ogromna większość ludności świata.
eche 24 CZERWCA 2022 14:31
Polityk rolna UE to jest wielki korupcyjny skandal.
wiesiek59 24 CZERWCA 2022 15:34
Chodziło tam o to, że przemysł USA nie wytrzymywał konkurencji ze strony Japonii i częściowo RFN. Niemcy jakoś sobie poradzili, ale Japonia wpadła w recesję, z której do dziś nie może się wydostać. Tak to jest, jak się ma Wujka Sama za Szefa.
PAK4 24 CZERWCA 2022 14:59
1. Rynek finansowy jest kontrolowany przez garstkę bardzo wpływowych „gnomów” z Wall Street w NYC, City of London i z Bahnhofstrasse w Zurychu.
2. Samochód marki np. VW złożony w Chinach, Polsce i Niemczech, jest dokładnie taki sam, ma taki sam wkład energii i pracy, gdyż to jest wciąż VW. Różnią sie one tylko jakością montażu.
3. Raczej sprzedają gospodarkę niemieckim obszarnikom i uciekają do miasta. Stąd też ten pozorny wzrost zamożności na polskiej wsi. Jest tam zresztą coraz mniej rolników w sensie „właścicieli ziemi”, a coraz więcej parobków pracujących dla Niemca, tyle że dziś parobek nie pogania konia a kieruje importowanym traktorem.
4. Nie udawaj głupka. Zniesławianie jest wszędzie karane i nie ma nic wspólnego z ograniczeniem wolności słowa. Każda wolność kończy się bowiem wtedy, kiedy zaczyna ona ograniczać wolność i prawa innych ludzi – tu do posiadania dóbr osobistych, do których zaliczana jest m. in. cześć jednostki.
Naruszenia w/w dóbr osobistych, do których zaliczana jest cześć jednostki, zabrania także Kodeks cywilny. W polskim prawie karnym, zniesławienie (pomówienie, obmówienie, oszczerstwo) jest to występek polegający na pomówieniu innej osoby, grupy osób, instytucji, osoby prawnej lub jednostki organizacyjnej niemającej osobowości prawnej o takie postępowanie lub właściwości, które mogą poniżyć ją w opinii publicznej lub narazić na utratę zaufania potrzebnego dla danego stanowiska, zawodu lub rodzaju działalności.
Prasa jest zaś zobowiązana do prawdziwego przedstawiania omawianych przez nią zjawisk. Granicą wolności słowa i wolności, także prasy etc., jest zaś zawsze kłamstwo, a oczywistość prymatu prawdy nad fałszem akcentowana jest także w orzecznictwie Sądu Najwyższego.
Poza tym, to faktem jest, że uprawiasz tu amerykańską propagandę za pieniądze lub inne korzyści materialne, de facto popierasz Tuska i twoim ulubieńcem jest de facto Joe Biden. Ponadto, to nie ma przestępstwa, jeżeli zarzut uczyniony niepublicznie jest prawdziwy oraz nie popełnia przestępstwa zniesławienia, kto publicznie podnosi lub rozgłasza prawdziwy zarzut, który służy obronie społecznie uzasadnionego interesu lub dotyczy postępowania osoby pełniącej funkcję publiczną, czyli taką jak Ty. A ja, jako emeryt, publiczną osobą ani domem NIE jestem, C.N.U.
Teraz na temat
Dzisiaj uczniowie kończą rok szkolny.
Być może wśród nich jest jakiś absolwent, który w przyszłości zasłuży na miano szalonego naukowca odkrywając to co nie zostało odkryte i zmieniając bieg historii dotychczas nieznanej.
Nauka wymaga wytrwałości i spokoju, ale jak tu być spokojnym kiedy wymyślono tak wiele wojskowego sprzętu i kierowanej amunicji.
Przed chwilą zobaczyłem w telewizorze wybuchy pocisków wystrzelonych z amerykańskiej armaty przez Ukraińców w kierunku Rosjan. To pierwsza taka super dokładna broń dalekiego zasięgu dostarczona przez USA, a mają być następne.
Brak tylko informacji jak wielkie zniszczenia poczyniła ta broń.
Miało być szybko, a widzimy jak jest. Są tacy co mówią o długotrwałym konflikcie. Jeśli jedni i drudzy nie dadzą za wygraną szybko nie będzie jednakże pod warunkiem, że nie zostanie uruchomiona jeszcze potężniejsza broń masowego zniszczenia.
Wówczas można będzie powiedzieć; szkoda tego wysiłku i czasu na naukę. Pocieszyć się można tylko tym, że zaczęły się wakacje, a nowy rok szkolny dopiero we wrześniu
Nie przeszedł cały tekst, niestety…..
Do dodania jeszcze.
Afery z ustalaniem LIBOR, karę poniosły pionki.
Afery z ustalaniem cen surowców, kary nie poniósł nikt.
Wolny rynek?
Chyba w bajkach dla ubogich duchem i wiedzą.
By kontrolować swiat potrzebna jest kontrola:
1-rynków finansowych
2-energetycznych
3-żywności
4-tras handlu międzynarodowego
Utrata któregokolwiek czynnika uniemożliwia dyktat.
Jestesmy w sytuacji zakwestionowania:
1-prymatu militarnego
2-pozycji walut zachodnich jako jedynego środka wymiany
3-utraty kontroli nad szlakami handlowymi
4-ustalania cen surowców poza kontrolą zachodnich giełd.
A to jest koniec Imperium.
Baumanowskie Interregnum się rozpoczęło.
A co do demokracji i szermierza wolności słowa.
Cierpiącego „za komuny” i dorabiającego sobie w radiu, telewizji, publikującego bardzo sensowne treści- wówczas:
Adam Szostkiewicz
24 CZERWCA 2022
13:59
@Rossi
Pan nie czyta, ale wie z góry: akurat polityki ukraińskiej – jak na razie – nie krytykuję, o czym można na moim blogu przeczytć. Krytykuję niezdarne próby Morawieckiego objęcia jakiegoś przywództwa w tej sprawie w UE. Rozważań TW nie komentuję.
===========
Symptomatyczna treść.
Lepiej być TW Mi6?
wiesiek59 24 CZERWCA 2022 16:56
Dlaczego cytujesz tego durnia?
Niemiecki prezydent zaproponował rozmowy w Mińsku … Tak sobie myślę prywatnie … nawet papież wzywa do powrotu do stołu … ale banderowcy zastrzelili członka swojej delegacji … bo chciał rozmawiać …
Kluczem do tego, tak, jak za czasów III Rzeszy jest jak największa kontrola i inwigilacja życia społecznego i gospodarczego. Tak jak w państwie Hitlera społeczeństwo obecnie otrzymuje odpowiednio spreparowany mit, np. o. elektromobilności, dekarbonizacji, informatyzacji , prawach LGBT, który po odpowiednim jego nagłośnieniu i przeforsowaniu staje się obowiązującą ideologią.
Funkcjonariusze propagandy wypracowują społeczny „mandat” do przeprowadzenia radykalnych kroków do realizacji mitu. Aparat przymusu w zalążku niszczy wszelkie obiekcje niepokornych i mających odmienne zdanie. Realizacja mitu jest tak „ważna” dla społeczeństwa , że żaden racjonalizm i żadne wartości moralne nie mogą zatrzymać zaplanowanych działań. Zbawczy „postęp ludzkości” nie może czekać i w jego imieniu można życie zwykłych podludzi wywrócić do góry nogami.
https://marucha.wordpress.com/2022/06/22/nadludzie-bez-munduru/
kalvarya01
24 CZERWCA 2022
16:58
To egzemplifikacja pewnego procesu.
Jak z mądrego, momentami błyskotliwego publicysty, robi sie…..
Taką przemianę obserwuje u wielu autorów.
Na przykład, Sierakowski zaczął szczekać na rozkaz.
Pecunia non olet?
Tak skorumpowano całą zachodnią lewicę, związki zawodowe.
Pozostały jedynie stare nazwy, opakowania, zawartość zmieniła się diametralnie.
kalvarya01
24 CZERWCA 2022
16:18
Ładna to bieda: niemal w każdej zagrodzie po kilka zachodnich aut, w tym już nie tylko używane, sprowadzone za parę euro, ale nówki jak spod igły…
ontario
24 CZERWCA 2022
18:04
Nie rozumiesz chyba SYSTEMU.
Co 8-10 lat zaczyna drastycznie rosnąć oprocentowanie wczesniej udzielonych kredytów.
I zaczyna się strzyżenie owiec.
Pretekst zawsze się znajdzie.
Obecnie jestesmy w tej fazie.
Większość mieszkań, maszyn rolniczych, nowych budynków gospodarskich, została kupiona na kredyt.
Wyczarowany z powietrza.
Pod zastaw REALNYCH dóbr.
Maszyn, ziemi, mieszkań.
Spora cześć kredytobiorców nie sprosta podwojonym ratom.
I O TO CHODZI.
Akty własności przepisane będa na banki.
I nie spodziewaj się od ludzi tam zatrudnionych jakiejkolwiek litości.
Ich premie zależą od wykazania się bezwzględnością.
Ile razy już to na świecie przerabiano, trudno policzyć.
ontario
24 czerwca 202
„aut, w tym już nie tylko używane, sprowadzone za parę euro, ale nówki jak spod igły…”
I pewnie wszystkie spłacone w całości gotówka nówką jak spod prasy drukarskiej? Ja przypuszczam, że wątpię. W US do 2008 z podobnym entuzjazmem mówiono o szczęśliwcach, którzy pokupowali masowo domki nówki jak spod igły. Wszystko jeszcze przed nami Polakami!
wiesiek59
24 CZERWCA 2022
12:21
kompletnie nie na „temat ” – ni w 5 ni w ponieważ ( co mnie nie dziwi )
Naukowy blog Polityki stal sie nienaukowy.
Naukowy … Tak sobie myślę prywatnie … to jak chlebak służący do noszenia granatów … w tym szaleństwie jest metoda …
@PAK4 – Postęp w US of A
Większością 5 do 3 Sąd Najwyższy kraju twych marzeń i adoracji, czyli Stanów Zjednoczonych Ameryki, uchylił właśnie wyrok w sprawie Roe vs. Wade, który niemal 50 lat temu zalegalizował aborcję. Gubernatorzy konserwatywnych stanów ogłosili wprowadzenie zakazu aborcji ze skutkiem natychmiastowym. Całkowity zakaz lub bardzo restrykcyjne prawo aborcyjne będą więc obowiązywały w 26 stanach i dotknie to ok. 40 milionów Amerykanek, 58 proc. osób w wieku rozrodczym.
Sędzia Clarence Thomas wprost wezwał do ponownego rozpatrzenia orzeczeń znoszących: ograniczenia dostępu do środków antykoncepcyjnych, zakaz kontaktów seksualnych między osobami tej samej płci i zakaz zawierania małżeństw przez osoby tej samej płci.
Komentarze:
- To w USA da się obsadzać sędziów w sądzie najwyższym wedlug klucza politycznego? Ito jest legalne? W światowej ostoi demokracji i praworządności?
- Jak tam z urlopem macierzyńskim? Najbogatszy kraj trzeciego świata.
https://wiadomosci.gazeta.pl/wiadomosci/7,114881,28619634,usa-sad-najwyzszy-uchylil-wyrok-roe-vs-wade-to-oznacza-zakaz.html#s=BoxOpImg1
Slawomirski 24 CZERWCA 2022 18:56
Ty też raczej specjalnie naukowy nigdy nie byłeś. 😉
eche 24 CZERWCA 2022 18:30
W USA to raczej domopodobne baraki w stylu wczesnego Baraka Obamy.
ontario 24 CZERWCA 2022 18:04
Pisałem przecież, że te „nówki jak spod igły” ma niemiecki szef, a te sprowadzone z Rajchu za kilka ojro to są fury polskojęzycznych parobczaków, pracujących dla Pana z Niemiec. Układy jak za Adolfa…
wiesiek59 24 CZERWCA 2022 17:56
Racja!
wiesiek59 24 CZERWCA 2022 17:50
Tak, ale czy to trafi do np. @PAK4?
BBC klamie
„Millions of women in the US will lose the constitutional right to abortion, after the Supreme Court overturned its 50-year-old Roe v Wade decision.”
Amerykanska konstytucja nic nie mowi o aborcji. Kongres ustanawia prawa a sad je interpretuje. BBC klamie.
kalvarya01
24 CZERWCA 2022
19:40
Wygnali mnie tutaj Szostkiewicz z Harmanem.
Slawomirski 24 CZERWCA 2022 19:58
Mnie też.
Slawomirski 24 CZERWCA 2022 19:56
UK nie ma konstytucji, ale mówi się tam o konstytucyjnych prawach w sensie praw podstawowych. Zrozum specyfikę UK – konstytucyjnego królestwa bez konstytucji.
Slawomirski 24 CZERWCA 2022 19:56
Amerykanki muszą więc rodzić dzieci, żeby potem „prawdziwi” Amerykanie mogli je zastrzelić w szkole.
kalvarya01
24 CZERWCA 2022
19:47
Przytakuję ci z pełną powagą. Oczywiście, w PRL-u fiat 126 p na przedpłaty i po odczekaniu kilku lat był lepszy od niemieckich gratów używanych dziś przez parobczaków.
Slawomirski
24 CZERWCA 2022
18:56
Warto by więc wprowadzić listę nicków zakazanych (jak u Szostkiewicza i innych), aby algorytm z automatu wyrzucał wpisy bez ich czytania.
eche
24 CZERWCA 2022
18:30
Nie masz pewności, więc sobie dworuj zdrów.
Ps. Jeśli można, jakiej produkcji gratem albo nówką jeździsz i czy kupiłeś za dodrukowane papierki?
Ps. 2. Osobiście wolę kupić choćby i używany grat, bo skoro za dodrukowane papierki, to zawsze warto papierek wymienić na grata.
wiesiek59
24 CZERWCA 2022
18:28
Rozumiem system, PiS/PO/SLD/PSL itd. kupią wyborców, dodrukowując papierków albo tak czy siak dopłacając do kredytów, ale zawsze twoim i moim kosztem.
ontario 24 CZERWCA 2022 20:19
Fiat 126 to był Fiat 500 – samochód który zmotoryzował Italię, ale z nadwoziem w nowym, brzydszym stylu. Dziś odpowiednikiem tego „Malucha” jest używany, kilkunastoletni VW Golf z kopcącym silnikiem Diesla – ulubiony pojazd polskojęzycznych parobczaków w niemieckiej służbie. Dzięki Wałęsie, Mazowieckiemu i Balcerowiczowi, Polak ze wsi nie musi już dziś jechać na roboty do Niemiec, bo te roboty rolne (w sensie pracy, zatrudnienia etc.) przyjechały do nich z Niemiec do Polski.
https://ofiary.ipn.gov.pl/ofi/z-archiwum-ipn/pracownicy-przymusowi/14295,Propagandowe-afisze-i-plakaty-III-Rzeszy.html
To może ten link zadziała:
https://ofiary.ipn.gov.pl/ofi/z-archiwum-ipn/pracownicy-przymusowi/14295,Propagandowe-afisze-i-plakaty-III-Rzeszy.html
wiesiek59
24 CZERWCA 2022
18:28
Ponadto jeszcze lepiej rozumiem system, ponieważ kilka milionów rodaków pracuje tam (na Zachodzie), a stara się wydawać tu (na Wschodzie).
Dziś tam za najgorszą pracę fizyczną dla osób bez matury płacą dwa, trzy razy tyle, co tu nauczycielom dyplomowanym z wyższym wykształceniem uniwersyteckim.
Akurat znajomy wrócił stamtąd, gdzie pracował zaledwie ponad 10 lat i pracą fizyczną wypracował sobie emeryturę w euro taką, jakiej tu by nie dostał, tyrając 100 lat.
kalvarya01
24 CZERWCA 2022
20:31
Tak czy owak, lepszy niemiecki grat, niż nowiuśki maluch 126 p kupiony na przedpłaty i wyczekany przez kilka lat i kosztujący kilka rocznych pensji.
Poza tym – na drogach coraz więcej nowiuteńkich zachodnich aut, które parobczaki kupiły bez przedpłat, bez czekania i w cenie za roczną pensję.
kalvarya01
24 CZERWCA 2022
20:33
To argument poniżej pasa. Porównujesz pracę niewolników zabijanych przez oprawców z dobrowolną i świetnie opłacaną pracą, o wiele lepiej opłacaną przez Niemców niż przez Polaków?
ontario 24 CZERWCA 2022 20:22
Warto by więc wprowadzić NIE TYLKO listę nicków trefnych czyli zakazanych (jak u Szostkiewicza i innych), aby algorytm z automatu wyrzucał wpisy bez ich czytania, ale aby także automatycznie wysyłał tenże algorytm do komputera posiadacza trefnego nicka wirus, który uniemożliwi mu pisanie antyreżimowych tekstów.
24 CZERWCA 2022 20:35
Gdyby tam został, to bidował by tak, jak przeciętny polski emeryt. Po prostu emerytury mają tam sporą nominalną wysokość, ale ponieważ ceny są tam znacznie wyższe niż w Polsce, to ich siła nabywcza jest taka, jak polskich emerytur – grass is always greener abroad (on the other side of the fence).
kalvarya01
24 CZERWCA 2022
20:46
Tak zapewne zrobią, jak piszesz o tym algorytmie.
OK.
W niedzielę byłem w Niemczech. Przez most na Nysie do Polski waliły tłumy Niemców (autami, pieszo). W Polsce na targowisku nad Nysą na towarach tylko ceny w euro, nie ma cen podanych w złotówkach, a przecież to Polska.
Polscy sprzedawcy w Polsce w ogóle z Polakiem po polsku nie chcą rozmawiać, uznają tylko niemiecki.
Na stacjach benzynowych kolejki aut z niemiecką rejestracją, Niemcy kupują benzynę, tankując do pełna. Auto za autem przez cały dzień.
Nawet „dziewczynki” przy polskiej drodze oczekują tylko na euro.
Biznes się kręci jak szalony z korzyścią dla Polaków.
ontario 24 CZERWCA 2022 20:39
Dziś Fiat 126 jest samochodem kolekcjonerskim (tzw. youngtimer), wartym o wiele więcej, niż używany VW Golf. Za roczną pensję można dziś kupić w Polsce nowy samochód typu Dacii Logan (ok. 60 tys. zł) ale tylko nie jedząc, nie pijąc i nie płacąc za mieszkanie. A jeśli zarabiasz dwa razy tyle, to nie kupisz już takiego rumuńskiego badziewia a tylko albo dobry używany samochód wyższej klasy, np. tak jak ja kilkuletnią Hondę Civic S, albo oszczędzasz kilka lat na zakup „nówki”.
ontario 24 CZERWCA 2022 20:41
Robotników z Polski, którzy pojechali ochotniczo do pracy w III Rzeszy, nikt nie zabijał, może tylko Alianci przy okazji bombardowań. Mieszkając kilka lat w Niemczech Zachodnich, przeczytałem sporo na ten temat i spotkałem tam sporo Polaków, którzy wyjechali na te roboty do Niemiec i później nie wrócili do Polski, bo się dobrze zaaklimatyzowali w Niemczech. Nie powtarzaj więc, tak jak np. @PAK4, kłamstw obecnej i PRL-owskiej reżimowej propagandy.
ontario 24 CZERWCA 2022 20:57
Bzdura. Tydzień temu bylem kilka dni w Niemczech i nic takiego na granicy nie widziałem, a przekraczałem ją nie autostradą, a tylko w Słubicach tuż przy centrum Frankfurtu nad Odrą i w Zgorzelcu tuż przy centrum Görlitz.
kalvarya01
24 CZERWCA 2022
21:06
Mój dziadek-niewolnik miał inne zdanie niż twoje, więc nie zarzucaj mi kłamstw.
W piątek we Wrocławiu stałem przy parkingu Korony i patrzyłem na ulicę oraz parking.
Nie zauważyłem śladu polskiej motoryzacji. Wszystkie auta (żadnych gratów, raczej kilkuletnie) niemieckie, japońskie, niewiele francuskich.
Polacy już niewiele się różnią od innych zachodnich nacji, jeśli chodzi o auta, ale przecież to tylko jeden z wyznaczników.
Polska istnieje raczej tylko w wyobraźni staruszków i paru nawiedzonych ziobrystów.
kalvarya01
24 CZERWCA 2022
21:11
Bzdura, ja byłem w Łęknicy/Bad Muskau, potem w Kromlau zwiedzałem park rododendronów, gdzie za piwo i kawę z lodem zapłaciłem ponad 8 euro.
ontario 24 CZERWCA 2022 21:13
Twój Dziadek nie jest reprezentatywny dla Polaków pracujących w Niemczech podczas II WŚ.
24 CZERWCA 2022 21:15
Dla mnie 8 ojro to jak 8 złotych. W „Rajchu” dla oszczędności nocowałem w hotelach ****. ;-)
kalvarya01
24 CZERWCA 2022
21:23
To nie ma znaczenia. Znaczenie ma to, że zarzuciłeś mi kłamstwo i powtarzanie propagandy. Ja wierzę dziadkowi-niewolnikowi.
kalvarya01
24 CZERWCA 2022
21:23
Dla mnie euro to euro, przelicznik jak w kantorze, za piwo i kawę zabuliłem ponad 35 zł. W Polsce bym za to kupił ponad 10 piw, ale nie żałuję, mina Niemki była nagrodą (Polak tak hojnie podaje 10 euro i nie oczekuje na resztę), cudowne.
olborski 13.28
Nie znałem, chociaż kilka razy byłem u Dziewońskiego w kawiarni na Nowym Świecie.
To (tu) się wszystko musi zmienić, ale tym razem jeszcze napiszę parę razy po staremu
PS. Nawet jak nie piszę, że pozdrawiam, to pozdrawiam
ontario 24 CZERWCA 2022 21:30
NIE kłamstwo, a powtarzanie reżimowej propagandy. A to są różne przewinienia.
ontario 24 CZERWCA 2022 21:35
To wcale dużo nie zapłaciłeś, szczególnie jak na Niemcy.
ontario 24 CZERWCA 2022 21:13
To co robisz w Polsce, jak ci się ona aż tak nie podoba? Wracaj więc do tej swojej Kanady, podobno pachnącej żywicą. A ja z Niemcami rozmawiam po angielsku, chyba że trafię na takiego matołka, co to nie zna żadnego obcego języka, to tylko wtedy po niemiecku.
ontario 24 CZERWCA 2022 21:35
Dziś w Milanówku w restauracji, tyle że dobrej, za piwo zapłaciłem PLN 10.
NIE porównuj też cen ze sklepów z cenami w knajpach!
ontario 24 CZERWCA 2022 21:35
Na resztę z EUR 10, to w Niemczech czekają w knajpie tylko dziady kalwaryjskie. ;-)
ontario 24 CZERWCA 2022 21:35
Dziś nie miałem przy sobie drobnych, a więc do rachunku za ok. PLN 100, który zapłaciłem kartą, dołączyłem jako napiwek banknot EUR 10.
ontario 24 CZERWCA 2022 21:13
W Szwajcarii, Austrii, Belgii, Holandii, Portugalii czy Irlandii, Norwegii albo też innej Finlandii albo Islandii czy też Danii, nie mówiąc już o np. Luksemburgu, też nie zauważysz śladu samochodów osobowych wyprodukowanych przez lokalną markę. Nawet w Australii nie produkuje się ich dziś. Ponadto, to Polacy nie należą do Zachodu, a tylko do Wschodu i dobrze, bo tylko Wschód ma obecnie przyszłość.
Dobre wieści z Ukrainy:
Siły ukraińskie dostały rozkaz, by wycofać się z Siewierodoniecka. Powiadomił o tym w piątek szef administracji obwodowej Serhij Hajdaj.
https://www.tokfm.pl/Tokfm/7,103086,28618908,koniec-bitwy-o-siewierodonieck-co-dalej-ekspertka-nie-ma-optymistycznych.html#s=BoxOpImg4
Jaro Kaczyński opuścił lawy rządowe. Ale jakoś dziwnie tego dokonał.
Normalny tryb odchodzenia z rządzenia to ogłoszenie dymisji przez premiera, podziękowanie odchodzącemu, przedstawienie następcy. Następnie razem jadą do prezydenta, który uroczyście wręcza akt dymisji, są konferencje prasowe…
A tu prezes oświadczył po prostu dziennikarzom PAP :
– już nie jestem w rządzie, prezydent o ile wiem zaakceptował. No i ceremoniał odbył się dopiero dwa dni później.
Kaczyński wyjaśnił, że musi się skoncentrować na tym, co jest dla
przyszłości Polski najważniejsze, czyli na utrzymaniu władzy.
Na miejsce Jarosława Kaczyńskiego wicepremierem i szefem Komitetu ds Bezpieczeństwa został szef MON, Mariusz Błaszczak.
Ten Kacz. On po kaczemu jak nie kwacze to gdacze
Komentarz (nie mój):
Tej wojny nie powinno być w Europie. Ukraina nie ma szczęścia do elit , tak jak Polska . Po rozpadzie ZSRR, Ukraina miała sznasę na rozwój i samodzielność . Jednak elity ukraińskie wepchnęły ją w banderyzm i zapewnienia globalnych korporacji , że XXI wieku może w Europie istnieć państwo rządzone przez garstkę ześwirowanych nacjonalistów , myślacych kategoriami Bandery, który takie państwo chciał stworzyć we współpracy z Hitlerem . To się nie mogło udać. Ukraina po raz kolejny zostałą oszukana przez własne elity polityczne, nie liczące się z realiami politycznymi. Ukraińcy nie mogą umierać za interesy oligarchów ukraińskich i cynicznych globalnych korporacji.
https://www.tokfm.pl/Tokfm/7,103086,28618908,koniec-bitwy-o-siewierodonieck-co-dalej-ekspertka-nie-ma-optymistycznych.html#s=BoxOpImg4
Dymisja Kaczyńskiego jak poddanie się faszystów azowców … złożył na własne ręce … Tak sobie myślę prywatnie … tak po kaczemu … nie będziesz miał innego … przede mną … ja jestem prawo …
Nie ma polskiej flagi w Katyniu … Tak sobie myślę prywatnie … jak kaczyzm … to my wzajemnie … rusofobia ma dwa końce … tam jest Rosja … ! szanujmy sąsiadów …
Liczby są graficzną formacją … liczenie na palcach rzeczywistością i pod kontrolą … Tak sobie myślę prywatnie … po co kombinować z rzeczywistością … abstrakcyjną …
Pierwszą jaskółką dostrzeżenia problemu nierówności płac, było ustalenie pensji minimalnej kierowców na trasach międzynarodowych.
Pomimo awantury, przeforsowano projekt i wcielono w życie.
Uszczupliło to kiesę polskich przedsiębiorstw transportowych, zyskali kierowcy.
Świat się nie zawalił.
Drugą jaskółką jest projekt europejskiej pensji podstawowej.
Czyli, kierunek po mojej mysli.
Nie może być tak, że za taką samą pracę różna płaca.
To niesprawiedliwe.
Takie różnice nie mają uzasadznienia.
Bez unifikacji przepisów, płac, podatków, UE nie ma sensu.
wiesiek59 25 CZERWCA 2022 7:02
Tak, Bez unifikacji przepisów, płac, podatków etc. UE nie ma sensu.
SŁOWIANIN STANISŁAW 25 CZERWCA 2022 1:16
To dobrze, że nie ma polskiej flagi w Katyniu, bo to jest dzieło goebbelsowkiej propagandy.
SŁOWIANIN STANISŁAW 25 CZERWCA 2022 1:16
Komentarz (nie mój) z „Wybiórczej”:
Nawet nie warto tego komentować , ale z drugiej strony trzeba zadać pytanie , dlaczego do dni dzisiejszego nie ma w polskiej stolicy pomnika ku czci ofiar bestialskiej zbrodni ponad stu tysięcy Polaków zamordowanych przez bandytów
czczonego na Ukrainie bohatera narodowego ! Gdzie polski honor , gdzie godność , bo to nie było 20 tys, ofiar bandytów strzelających w głowę , to było grubo ponad 100 tyś, zamordowanych kobiet ,dzieci ,całych rodzin siekierami, widłami ! Dlaczego parszywa władza stara się o tym zapomnieć !?
SŁOWIANIN STANISŁAW 25 CZERWCA 2022 1:32
Tym razem na temat tego wątku: liczby są „czystą” abstrakcją, tak jak np. duchy (w tym święte), bogowie, boginki, prawo, sprawiedliwość, mądrość, głupota etc. etc. Można więc na nich wykonywać takie działania, jakie się chce – to jest tylko kwestia przyjęcia takich a nie innych dogmatów (pewników, aksjomatów etc.).
Ukłony.
Z „Wybiórczej”:
W nocy z piątku na sobotę doszło do strzelaniny w centrum Oslo. Jak podają norweskie media, strzały padły w dwóch miejscach, w tym przed „London Pub”, klubem dla osób LGBT. Zginęły dwie osoby, a 19 zostało rannych, w tym trzy ciężko. Na razie nie jest znany motyw działania sprawcy.
Z aksjomatami tez nie jest tak prosto jak pokazuje Aksjomat Wyboru (Axiom of Choice). Vide np. Paradoks Banacha-Tarskiego i dwa systemy ZF vs ZFC. Sam Euklides zrezygnowal z jakchis, bo mozna je bylo udowodnic poprzez inne albo staly w sprzecznosci z innym I, nie wiem.
Fun and games. Z jednym zastrzezeniem: liczby jakos ‚istnieja’, zielone jednorozce nie, sa tylko rozowe.
act 25 CZERWCA 2022 8:50
W moim wirtualnym Universum „istnieją” tylko zielone jednorożce, a jak wiadomo, geometria Euklidesa opisuje nieistniejący „płaski” Wszechświat, a więc jest ona z gruntu rzeczy błędna. Wyrządza się więc wielką szkodę dzieciom, ucząc ich w szkole tej, z gruntu rzeczy fałszywej, geometrii z „ciemnej” epoki niewolnictwa. 🙁
Ukłony etc.
Podobno ‚the Universe is flat’ i twierdzenie Pitagorasa dziala w kazdym kierunku (tak m. in. definiuje sie plaskosc przestrzeni Wszechswiata)… ale the jury is still out on that one.
kalvarya01 24 czerwca 2022 22:48
Ciekawi mnie dlaczego we wschodnich obwodach Ukrainy narodowość ukraińską deklarowało 60 -70% mieszkańców ale znacznie mniej, bo tylko 25 – 50% deklaruje posługiwanie się na co dzień językiem ukraińskim.
To kim oni są – Rosjanami czy Ukraińcami.
Są to dane ze spisu powszechnego na Ukrainie z 2001 bo w 2011 zaniechano spisu, gdyż wielu respondentów odmawiało odpowiedzi a w 2021 wcale nie podjęto nawet próby spisu powszechnego.
Dlaczego w 2011 tak wiele osób odmawiało odpowiedzi ?
Wg mnie ZE STRACHU , gdyż widocznie już wtedy nacjonalizm ukraiński i różne restrykcje wobec osób deklarujących nieukraińską narodowość były przez tych ludzi odczuwane.
Donbas idzie w kierunku Śląska … II RP też wspierała militarnie … Tak sobie myślę prywatnie … nie wstydżmy się tych faktów … naród chroniony od poczęcia … przez macierz … za miedzą …
Czy Ukrainiec to narodowość czy administracyjne określenie mieszkańca Republiki ZSRR … przejęte przez społeczność międzynarodową jak jankes … Tak sobie myślę prywatnie … Rusin przybliża do korzeni … Rusi Kijowskiej …
kalvarya01 25 czerwca 2022 9:25
Jak na razie maksymalna prędkość, jaka osiągnął pojazd zbudowany przez ludzi ( Boeing X-43 ) stanowi 1/100 000 prędkości światła. Oczywiście był to pojazd bezzałogowy, gdyż człowiek może znieść przyspieszenie maks. 5 g . Można wiec sobie policzyć ile czasu potrzeba, by się do tej prędkości rozpędzić – z grubsza ponad miesiąc. Skąd zresztą wziąć tyle paliwa ( jakiego ? ) dającego potrzebną ilość energii itd., itd….
Zajmijmy się problemami REALNYMI.
@kalvarya01:
Nie wiem, czy z czymkolwiek się zgodziłbym, ale tu wywołałeś u mnie :LOL:
> 2. Samochód marki np. VW złożony w Chinach, Polsce i Niemczech, jest dokładnie taki sam, ma taki sam wkład energii i pracy, gdyż to jest wciąż VW. Różnią sie one tylko jakością montażu.
Piszesz się, że jesteś doktorem habilitowanym w zakresie nauk o ekonomii i zarządzaniu i nie zauważasz wpływu organizacji produkcji na energię i pracę włożoną w wytworzenie samochodu? To ja powiem więcej: nie tylko organizacja produkcji, ale także automatyzacja linii przemysłowej, kompetencje pracowników, kwestie kulturowe, jak oczekiwany poziom nadzoru nad pracownikami.
Tu już chyba nie muszę dodawać, że energia też nie jest uniwersalna, ale jej koszt zależy od rozwiązań na danym terenie. Że poddostawcy mogą być bliżej lub dalej; albo że dostępność zasobów naturalnych jest różna…
@kaesjot:
Voyager 1 ma bodaj 61 tys. km/h.
@PAK4
Niemniej jest to 18 tys. Razy wolniej niż wynosi prędkość światła.
kaesjot,
wlasnie obliczylem, circa 1704 tys. razy 🙂
widzialem w Smithsonian bodaj X-15,
‚Enole Gay’ tez niestety, na rok przed jej wyrzuceniem stamtad po 3 letnich protestach, 1995 – 1998.
17, 704 razy, nie tysiecy razy!!! do tego uciekla mi jedna ‚7’, sorry.
PAK4 25 CZERWCA 2022 11:44
Jeśli się na czymś nie znasz, to nie pchaj się na publiczne forum (blog) ze swoją niewiedzą. Powtarzam – Samochód marki np. VW złożony w Niemczech, Australii czy Meksyku, jest dokładnie taki sam, ma taki sam albo bardzo zbliżony wkład energii i pracy, gdyż to jest wciąż VW. Różnią się one tylko jakością montażu, gdyż tego nie da się ”z góry” zarządzić, tak jak można np. „zadekretować” np. ilość czasu i energii potrzebnych na każdą operację w ramach procesu technologicznego produkcji samochodu. Zauważ, że ja piszę o samochodzie VW, a więc produkowanym wszędzie wedlug standardów VW, a nie porównuję, tak jak ty, jabłek z pomarańczami, co jest zresztą typowym błędem popełnianym przez tzw. humanistów, czyli inaczej wykształciuchów. Organizacja produkcji a więc też energia i praca włożona w wytworzenie samochodu np. VW Golf GTI pierwszej generacji (wiem że już go nie produkują, ale to nie jest tu istotne) są więc z grubsza takie same w Wolfsburgu, Brukseli, Melbourne, New Stanton, Shah Alam czy Puebla (a jeśli jest inaczej, to się taki mało wydajny zakład zamyka, np. montownię VW w Melbourne). Inaczej to nie bylby to VW Golf GTI, a tylko wyrób „golfopodobny” – tak jak to było np. Fiatem 125P, ktory po spadku jego jakości stał się FSO 1500. Tam wszędzie, jak to napisałem powyżej, są lub były fabryki VW, a więc zarówno organizacja produkcji, poziom automatyzacji linii produkcyjnej (NIE „przemysłowej”), kompetencje pracowników, jak i oczekiwany poziom nadzoru nad pracownikami sa więc w zasadzie takie same, a kwestie kulturowe ograniczają sie tu do tzw. korporacyjnej kultury VW.
Energia też jest tyko jedna, czyli uniwersalna, równoważna masie, tyle że w różnych postaciach, ale np. energia elektryczna może być zamieniona w chemiczną i przechowywana w akumulatorze, po czym znów zamieniona w energię elektryczną, ale to jest wciąż ta sama energia, minus jej nieuniknione straty przy każdej transformacji jej postaci (termodynamika, o której zresztą też nie masz pojęcia, się tu kłania). Koszt energii jest oczywiście różny w różnych państwach czy regionach, stąd też energochłonne fabryki, np. huty aluminium, umieszcza się na ogół w pobliżu wielkich elektrowni, produkujących możliwie tanią energię elektryczną. Ale w przypadku produkcji samochodów ważniejsze są wciąż koszta robocizny i bliskość rynków zbytu. Jak widać, nie masz też pojęcia o geografii ekonomicznej…
Poddostawcy dla producenta samochodów ulokowanego np. w Kanadzie, mogą być zaś dziś np. w Chinach albo Argentynie, a surowce naturalne, takie jak np. rudy metali, wozi się dziś niemalże dookoła świata. A więc wróć do swych „gander studies”, czyli studiów nad gąsiorami i nie kompromituj się na tym blogu, please…
act 25 CZERWCA 2022 13:12
Też widziałem (pod koniec ubiegłego stulecia) w Smithsonian (dokładniej w National Air and Space Museum w Washington DC) X-15 (dokładniej The North American X-15 rocket-powered research aircraft) i nawet pogadałem sobie z jego pilotem. Zgodziliśmy się też, jak to pilot z pilotem (ja szybowca a on ponaddźwiękowego rakietowego super-samolotu, czyli rakietoplanu), że monarchia jest dziś przeżytkiem. 😉
https://www.si.edu/object/north-american-x-15%3Anasm_A19690360000
Ukłony etc.
act 25 CZERWCA 2022 13:12
Też widziałem (pod koniec ubiegłego stulecia) w Smithsonian (dokładniej w National Air and Space Museum w Washington DC) X-15 (dokładniej The North American X-15 rocket-powered research aircraft) i nawet pogadałem sobie z jego pilotem. Zgodziliśmy się też, jak to pilot z pilotem (ja szybowca a on ponaddźwiękowego rakietowego super-samolotu, czyli rakietoplanu), że monarchia jest dziś przeżytkiem. 😉
Patrz pod „North American X-15 National Air and Space Museum”.
Ukłony etc.
PAK4 25 CZERWCA 2022 11:44
Powtarzam – jeśli w danym miejscu produkcja danego modelu np. samochodu okazuje się zbyt pracochłonna lub zbyt energochłonna, albo jeśli jakość wyrobu wyraźnie nie jest taka, jaka powinna być, to się go przestaje w tym miejscu produkować. Tak więc samochód marki np. VW powiedzmy Tornado (nazwa zmyślona, gdyż jest tylko kolor „Volkswagen Tornado Red”), złożony (znów przykładowo) w Chinach, Polsce czy Niemczech musi mieć dokładnie, no powiedzmy prawie dokładnie taki sam, aby się znów nie czepiał detali, wkład energii i pracy, aby opłacało się go produkować w danej lokalizacji.
PAK4 25 CZERWCA 2022 11:44
Na koniec – to są oczywiście tylko ogólne zasady, od których są wyjątki. Np. dane państwo wprowadza zaporowe bariery celne na import, a więc globalny koncern zakłada tam swoją wytwórnię, nawet jeśli na początku do niej dopłaca, aby utrzymać rynek czy też na niego wejść, albo też kiedy np. Korea Południowa zaczęła produkować samochody, to aby wejść na rynki światowe, rząd tejże Korei Południowej dopłacał na koszt podatników wytwórniom południowokoreańskim, gdyż inaczej, to nie wytrzymały by one konkurencji na rynkach zagranicznych. To się nazywa wspomaganiem przez państwo tzw. infant industries, a czego Polsce nie wolno jest robić w ramach UE.
@PAK4
Chiny zrzucają etykietę słabeusza, by stać się potęgą kosmiczną
Andrew Mullen, zastępca redaktora naczelnego, Ekonomia Polityczna
„South China Morning Post” z dnia 25 czerwca 2022 roku.
Mówi się, że przestrzeń kosmiczna to ostateczna granica. Ale jak daleko sięga ta granica i co się tam znajduje? W ostatnich latach Chiny przyspieszyły działania związane z przestrzenią kosmiczną w ramach swojego intensywnego programu naukowego, o którym pisaliśmy kilka tygodni temu, od lądowania łazika na Marsie po bliskie ukończenie stacji kosmicznej Tiangong. W tym numerze Stephen Chen z SCMP, redaktor ds. nauki w naszym dziale w Chinach, powraca, by przyjrzeć się wyczynom Chin i zastanowić się nad przyszłością ich ambitnego programu kosmicznego.
Astronautka Liu Yang odrzuciła prośbę swoich dzieci, by pomachać jej na pożegnanie przy stanowisku startowym. „Mama idzie na wojnę” – napisała pierwsza Chinka w kosmosie w liście pożegnalnym, napisanym tuż przed misją Shenzhou 14, która wysłała ją w kosmos po raz drugi. Jako żołnierz na służbie, w obliczu zagrożenia muszę zapomnieć o rodzinie. Obawiam się, że będę płakać, gdy was zobaczę – dodała.
Pułkownik Liu i jej dwaj męscy członkowie załogi spędzą na orbicie sześć miesięcy, kończąc budowę stacji kosmicznej Tiangong, najbardziej zaawansowanej infrastruktury zbudowanej przez jeden naród w przestrzeni kosmicznej. Intensywność pracy będzie większa niż podczas poprzednich misji, choć będą musieli uważać na niespodziewanych gości, takich jak nieprzyjazne satelity, które mogą stanowić zagrożenie dla ich życia. Chiny do niedawna były przegraną stroną w wyścigu kosmicznym, po tym jak odrzucono ich prośbę o dołączenie do 15 innych narodów w starzejącym się programie Międzynarodowej Stacji Kosmicznej. Ich wysiłki były nieco utrudnione z powodu międzynarodowych sankcji, a chiński przemysł kosmiczny był zmuszony budować prawie wszystko sam. Z tego samego powodu niewiele państw wystrzeliło satelity za pomocą chińskich rakiet, mimo że są one zaawansowane technicznie, stosunkowo tanie i wysoce niezawodne.
Nie przeszkodziło to Chinom w przeprowadzeniu w ostatnich latach większej liczby startów kosmicznych niż jakikolwiek inny kraj, po tym jak naukowcy i inżynierowie opracowali rakiety nowej generacji, mimo początkowych niepowodzeń. Zbudowali także pierwszego na świecie satelitę kwantowego, choć niektórzy uważali, że ta technologia nie zadziała. Najnowszymi osiągnięciami chińskich naukowców są także najdokładniejsze zegary atomowe w kosmosie, najszybsze eksperymenty z komunikacją laserową, najzwinniejszy satelita obrazujący oraz najpotężniejsze kosmiczne urządzenie laserowe. Wylądowali oni również pierwszym statkiem kosmicznym na dalekiej stronie Księżyca.
Podczas pierwszej wizyty Chin na Marsie, cmentarzysku wielu wcześniejszych misji innych krajów, udało im się umieścić na powierzchni łazik, bez wcześniejszej znajomości czerwonej planety. Jednak chińskie władze kosmiczne mają większe ambicje. Wspólnie z Rosją chcą zbudować międzynarodową stację badawczą na Księżycu, a misja pobrania próbek z Marsa planowana jest na 2031 r., dwa lata przed misją NASA. W ramach eksperymentu ratowania Ziemi chiński statek kosmiczny uderzy w dużą asteroidę, aby zmienić jej kurs. Z kolei kosmiczna elektrownia słoneczna będzie bezprzewodowo przesyłać energię do niemal każdego miejsca na powierzchni naszej planety. Aby osiągnąć te cele, chińscy naukowcy opracowują kilka rewolucyjnych technologii.
Do 2035 r. planują zbudować flotę hipersonicznych samolotów kosmicznych, które będą mogły przewozić tysiące pasażerów na niższą orbitę okołoziemską rocznie, a ich koszt będzie znacznie niższy niż koszt rakiet. Kilka opracowywanych obecnie kosmicznych reaktorów jądrowych może wytwarzać ponad jeden megawat energii na potrzeby podróży międzygwiezdnych lub osadnictwa. System obrony planetarnej składający się z ogromnej sieci radarowej będzie monitorował śmieci kosmiczne i wykrywał zagrożenia związane z asteroidami z niespotykaną dotąd dokładnością i terminowością.
Wzrost znaczenia Chin jako potęgi kosmicznej nie zawsze był jednak dobrze przyjmowany. Niektórzy naukowcy wzywali wojsko do zniszczenia największej na świecie internetowej sieci satelitarnej, jeśli stanowi ona zagrożenie dla bezpieczeństwa narodowego Chin. Nowe chińskie satelity są wzmocnione dodatkową osłoną przed nowymi rodzajami broni kosmicznej, takimi jak mikrofale o dużej mocy, które mogą zakłócić komunikację lub spalić czujniki i chipy. Tuż przed startem Liu znaleziono urządzenie zagłuszające w pobliżu miejsca startu na pustyni Gobi, choć nie było jasne, czy odkrycie to było próbą sabotażu czy przypadkiem.
Nie bójcie się niepowodzeń – powiedziała Liu swoim dzieciom w liście. „Po prostu róbcie to jeszcze raz, i jeszcze raz”.