Nieprawdopodobna prawda o prawdopodobieństwie w kontekście zbiorów nieskończonych

22 maja 2019
Blog szalonych naukowców

W komentarzach do jednego z moich poprzednich wpisów wypełzł problem prawdopodobieństwa. Oto wybitny ewolucjonista Richard Dawkins w swojej książce „Bóg urojony” (najsłabszej moim zdaniem z dotychczas przeze mnie przeczytanych) pisze o prawdopodobieństwie istnienia Boga. Dochodzi do wniosku, że prawdopodobieństwo to prawie na pewno wynosi 0. A więc że Bóg nie istnieje? Czego się czepiać?

Zastanówmy się więc, co właściwie oznacza prawdopodobieństwo. Definiuje się je rozmaicie. Jedna z prostszych definicji wprowadza pewien skończony zbiór wszystkich możliwości (tzw. zdarzeń elementarnych). Prawdopodobieństwo zajścia A wyznacza iloraz liczności dwóch zbiorów: zbioru zdarzeń sprzyjających A do liczności zbioru wszystkich zdarzeń elementarnych. Przykład: rzucamy kostką do gry. Jakie jest prawdopodobieństwo wyrzucenia liczby podzielnej przez 3? Mamy w naszym zbiorze 6 zdarzeń elementarnych (wyrzucenie każdej z cyfr), spośród których 2 (wyrzucenie 3 lub wyrzucenie 6; tak: lub, nie i) sprzyjają rozpatrywanemu zdarzeniu. Prawdopodobieństwo P wynosi 2/6.

Proste? Tak, i dlatego matematycy tej definicji nie użyją. Wprowadzili rozmaite inne ujęcia, np. częstotliwościowe czy oparte na przedziale <0;1> (czyli liczb rzeczywistych od 0 do 1), a nawet na ciągach i przestrzeni probabilistycznej, czymkolwiek by ona była. Wbrew pozorom w matematyce jest dużo dziwnych pojęć i aż dziw, że wszystkie one wymagają niewielkiego w sumie zestawu aksjomatów.

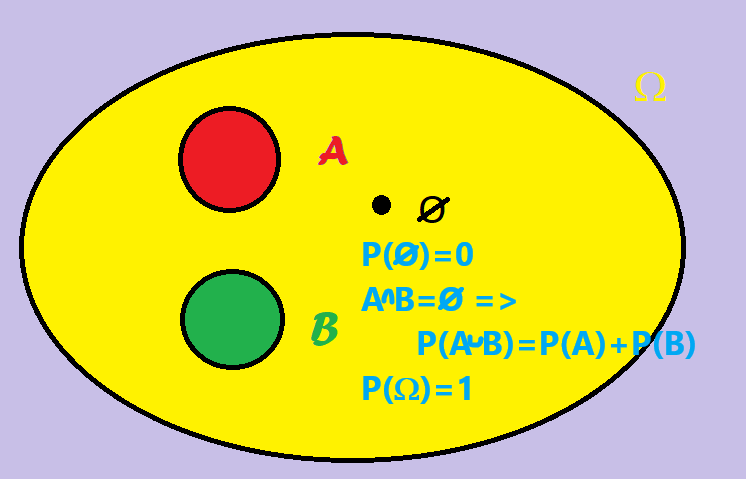
Jedna z ciekawszych definicji definiuje prawdopodobieństwo jako pewną miarę… zatrzymajmy się. Czym jest miara? Jeżeli mamy pewien obrany zbiór (nazwijmy go Ω), to miara jest funkcją przyporządkowującą jego podzbiorom pewne liczby (czyli funkcją ze zbioru potęgowego P(Ω) w pewien podzbiór R). Pierwsze ograniczenie: przyporządkowywane liczby rzeczywiste muszą być nieujemne (czyli dodatnie lub 0). Matematyk, który nie po to jest matematykiem, żeby używać słów (bo jeszcze ktoś niepowołany, np. polonista, by go zrozumiał), napisze: μ(x) ∈ [0;∞).

Drugie ograniczenie wymaga wprowadzenia pojęcia zbioru pustego. To zbiór, do którego nie należy żadne zdarzenie (w ogóle nic do niego nie należy, jak sama nazwa wskazuje). Wbrew pozorom wzór taki przydaje się w matematyce, a jego istnienie gwarantują założenia teorii zbiorów. Temu zbiorowi przyporządkowujemy liczbę 0 (jaką inną liczbę przyporządkować zbiorowi, w którym nic nie ma?). Matematyk zapisze μ(∅) = 0. Trzecie ograniczenie: w przypadku pary zbiorów nieposiadających wspólnych elementów miara ich sumy jest równa sumie ich miar. Matematycznie: (A ∧ B = ∅) ⇒ μ(A ∨ B) = μ(A) + μ(B). Żebyśmy mogli mówić o prawdopodobieństwie, musimy dodać jeden warunek: miara musi przypisywać całemu zbiorowi Ω wartość 1.

Skąd takie warunki? Po pierwsze, prawdopodobieństwo nie może być mniejsze od 0. Po drugie zdarzeniu, które nigdy nie zachodzi (zbiór pusty), przypisujemy prawdopodobieństwo 0. Po trzecie, prawdopodobieństwo dwóch zdarzeń niezależnych (np. wyrzucenie kostką 2 lub 3) jest równe sumie prawdopodobieństw tych dwóch zdarzeń. Po ostatnie zaś – prawdopodobieństwo nie może być większe od 1.

Ten ostatni warunek odgrywa dużą rolę m.in. w mechanice kwantowej. Taki elektron np. nie zajmuje żadnego konkretnego miejsca i opisać go można jedynie funkcją falową określaną literą psi, Ψ (kojarzy się z czymś dziwnym najzupełniej słusznie). Co oznacza Ψ? Ano nie bardzo wiadomo, co oznacza. Ale jeśli się weźmie jej moduł (czyli odległość liczby będącej wartością funkcji od liczby 0, najprościej mówiąc) i podniesie do kwadratu, otrzyma się gęstość prawdopodobieństwa.

Inaczej mówiąc, jeśli mamy wykres tego dziadostwa i chcemy policzyć prawdopodobieństwo, że elektron znajdzie się między wartościami x1 a x2, to liczymy pole pod wykresem kwadratu modułu Ψ między x1 a x2 (matematycy nazywają to całkowaniem, jak widać, służy ono nie tylko do dręczenia studentów). Czasem pojawia się problem, którą z możliwych funkcji Ψ wybrać? Ma ona określać prawdopodobieństwo znalezienia cząstki, którą na pewno gdzieś znajdziemy. Prawdopodobieństwo znalezienia elektronu gdziekolwiek wynosi 1 i tyle samo musi wynosić pole powierzchni pod całym wykresem funkcji (od – nieskończoności do + nieskończoności).

Prawdopodobieństwo jest bardzo wdzięcznym narzędziem w przypadku zbiorów skończonych. W przypadku zbiorów nieskończonych urządza rozmaite hece. Ale komu potrzebne jakieś nieskończoności? Otóż pojawiają się one częściej, niż się wydaje. Rozpatrzmy zwykły odcinek. Obejmuje on nieskończenie wiele punktów. Nazwijmy odcinek AB i przedzielmy go na dwie części w stosunku 1:2 punktem C. Wybierzmy teraz 1 z punktów tworzących ten odcinek. Jaka jest szansa, że znajdzie się w części AB? Proste: 1/3. No dobra.

Osadźmy odcinek w układzie współrzędnych starego dobrego Kartezjusza (ale sztuczki będziemy robić raczej wzorem Cantora). Niech leży na osi X, punkt A niech ma współrzędne -1, C – 0, a B – 2. Wtedy każdemu punktowi na odcinku przyporządkować możemy liczbę rzeczywistą z przedziału <-1;2>. Jakie jest prawdopodobieństwo wylosowania punktu z części AC (zbiór <-1;0>)? Niezmiennie 1/3.

No dobra, bierzemy sobie te punkty (możemy to zrobić na gruncie wspomnianych aksjomatów teorii zbiorów) i stosujemy do każdego taką funkcję: bierzemy wartość na osi x, na której leży dany punkt, i mnożymy przez 2. Każdą liczbę rzeczywistą można pomnożyć przez 2 i zawsze otrzymamy inną liczbę, zrobiliśmy to dla każdego naszego punktu ze zbioru AC, więc liczba punktów nie zmieniła się. Co więcej, każda liczba rzeczywista z przedziału <-2;0> jest dwukrotnością pewnej liczby rzeczywistej z przedziału <-1;0>, wobec tego otrzymaliśmy zbiór <-2;0>.

Każde dwa zbiory mają swoją sumę (to kolejny aksjomat teorii zbiorów). Dodajmy więc otrzymany zbiór do wcześniejszego, odpowiadającego punktom odcinka CB. Otrzymamy przedział <-2;2>. Jakie jest prawdopodobieństwo, że wylosowany teraz punkt będzie należał do zbioru otrzymanego z AC? Czyżby… ½? Ale przecież liczba punktów się nie zmieniła, zmieniliśmy tylko etykiety? Tak, możemy je zmienić dowolnie i otrzymać jeszcze bardziej fantazyjny wynik, jaki nam się właściwie podoba – od 0 do 1.

To teraz jeszcze lepsza sztuczka. Weźmy kwadrat o boku 1, położony w lewym dolnym rogu w środku układu współrzędnych. Wybierzmy z niego 1 punkt. Jakie jest prawdopodobieństwo, że trafimy w punkt leżący na osi x? Wynosi ono 0 (1 punkt z nieskończoności). To teraz weźmy wszystkie punkty tego kwadratu (możemy pominąć jego górny i prawy bok). Każdy z nich ma współrzędne x i y wyrażone liczbami rzeczywistymi, czyli nieskończonymi ciągami cyfr 0,Cx1Cx2Cx3… i 0,Cy1Cy2Cy3… Ustawmy te cyfry na przemian w rozwinięciu dziesiętnym trzeciej liczby: 0,Cx1Cy1Cx2Cy2Cx3Cy3… Czyli każdy punkt należący do kwadratu otrzymuje etykietę, etykiety te razem tworzą… zbiór <0;1), czyli dolny bok kwadratu. Istotnie: wszystkie punkty kwadratu zmieścić można na jednym jego boku, oba zbiory mają tyle samo punktów (c, od łacińskiego continuum). Mamy dwa zbiory o tej samej liczności i wybór elementu z jednego z nich ma prawdopodobieństwo 0, a drugiego – 1?

Otóż w przypadku zbiorów nieskończonych prawdopodobieństwo danego zdarzenia nie jest immanentną cechą zbioru i zdarzenia, ale zależy od sposobu wyboru zdarzenia. Wybierając fantazyjnie, można prawdopodobieństwem pomanipulować. W szczególności zaś nie ma sensu mówienie o prawdopodobieństwie, jeśli wybieramy ze zbioru nieskończonego, a nie określimy, w jaki sposób wybieramy element.

Jeszcze mniejszy sens ma mówienie o prawdopodobieństwie bez wskazania zbioru, któremu przypisujemy wartość 1. Jeśli nie opiszemy tego porządnie, zgubimy się już w przypadku niewielkiego (acz liczącego nieskończenie wiele punktów) odcinka. Tym bardziej gdy próbujemy liczyć prawdopodobieństwo istnienia Boga, nie określiwszy w ogóle zbioru Ω. Równie dobrze mógłbym napisać, że prawdopodobieństwo błędu w takich sformułowaniach dąży do 1. W matematyce bardzo istotne są założenia. Nie przywiązując do nich uwagi, popełnimy błąd, jak mówią niektórzy, na 300 proc.

Grafika wykonana przez autora.