Ku pokrzepieniu serc – przed maturami
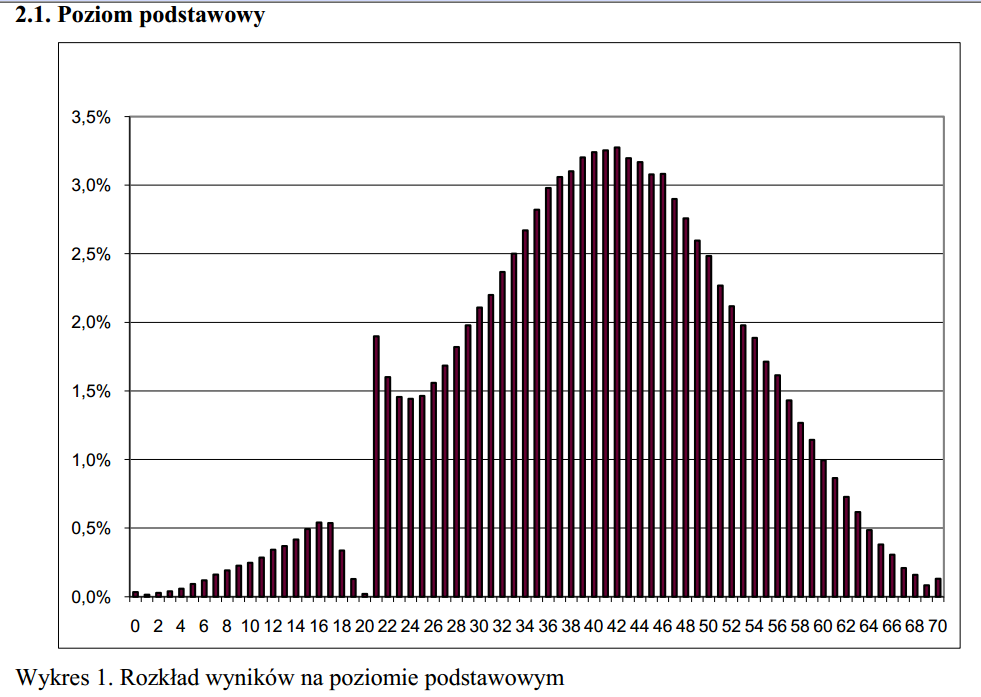
Poniższy wykres to histogram wyników punktowych w maturze podstawowej z języka polskiego w 2010 roku. Oś pozioma to wynik punktowy, wysokość słupka wskazuje ile procent zdających uzyskało taki właśnie wynik.
Wykres znajduje się w dokumencie „Osiągnięcia maturzystów w 2010 roku”, opublikowanym przez CKE (szczegóły na dole). Moim zdaniem to jednak przede wszystkim wielkie osiągnięcie sprawdzających. Jak widać, praktycznie każdemu uczniowi, który powinien był dostać 20 punktów zdołali dopisać co najmniej jeden dodatkowy punkt. Większości tych, którzy powinni byli dostać 19 punktów udało się dopisać nawet dwa dodatkowe punkty. Tajemnica tej anomalii to oczywiście granica 30%, czyli w tym wypadku 21 punktów, która pozwala uznać maturę za zdaną.
I jak się teraz oprzeć wrażeniu, że kryteria oceniania matur z polskiego są całkowicie uznaniowe?
Ale to nie koniec: przyjrzyjmy się jeszcze raz tym wynikom. Wyglądają prawie idealnie jak krzywa Gaussa (z anomalią w okolicach 21 punktów), co sugeruje, że wynik matury z tego przedmiotu zachowuje się jak suma wielu niezależnych zmiennych losowych o niewielkim wkładzie jednostkowym. Jeśli to prawda, to sugeruje, że umiejętności sprawdzane w poszczególnych zadaniach na maturze są ze sobą niepowiązane (co najmniej statystycznie). Czy to dobry znak – ja uważam, że wręcz odwrotnie. No chyba że ta niezależność i losowość to głównie dzieło losowo przydzielających punkty sprawdzających, bo że kryteria są uznaniowe, to już zauważyliśmy.
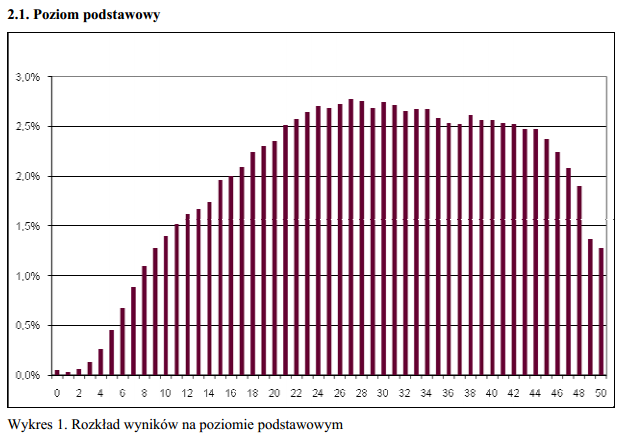
Co jeszcze ciekawsze, wyniki matury podstawowej z matematyki, która w tym właśnie roku 2010 na powrót stała się obowiązkowa, nie wykazują takich anomalii: ani uskoku, ani kształtu krzywej Gaussa.
Jerzy Tyszkiewicz
Ilustracje z dokumentu „Osiągnięcia maturzystów w 2010 roku”, na prawach cytatu.
Zainspirowałem się wpisem z forum Demotywatory.

Komentarze
Ocena z matematyki jest bardziej „zobiektyzowan”?
Z poważaniem W.
Wygląda ten wykres jak leżący spinozaur z odciętą głową 🙂
Ja bym na sprawdzanie różnych rzeczy przez różne zadania nie narzekał.
Tak na marginesie, ten obrazek dyskutowano ponad rok temu na blogu Polityki Belfer Blog.. .
A wymowa? Oczywiscie, „podciaga” sie oceny bedace „na krawedzi”. W trosce o statystyke i na zasadzie „co mi tam zalezy zeby facia oblac”
Jezeli ktos z P.T. Nouczycieli Akademickich nigdy tego nie robil, prosze podniesc reke
Odnoszę wrażenie, ze problemem jest to, ze wiecie panowie zbyt mało o maturze z polskiego i matematyki, aby zrozumieć dlaczego wykresy maja taki kształt. Dość powiedziec, ze cześć zadań z matematyki (za polowe punktów) sprawdzana jest maszynowo, a tylko cześć prze egzaminatorów. W związku z tym tzw. Efekt egzaminatora ukrywa sie wewnątrz rozkładu.
@A.L.
Czy czytał Pan maila od redakcji?
@Endo
Wręcz odwrotnie – po obejrzeniu wykresów dowiedziałem się o nich całkiem dużo, mimo że przedtem niewiele miałem z maturami kontaktu.
Nawet jeśli połowę punktów z matematyki przydziela maszyna, to drugą połowę daje człowiek, a mimo to nie widzę efektu „dopychania” przez ludzi-sprawdzających do granicznych 30%. Zatem należy przyjąć, że sprawdzający tego nie robią. Dlaczego tego nie robią – to osobna kwestia i tego rozstrzygnąć nie potrafię.
Poniewaz dostale od wlascicieli bloga dozywotniego „bana”, chcialbym pozegnac zie z tymi z ktorymi dobrze mi sie dyskutwoalo, w szczegolnosci kaganowi i zza kaluzy, podziekowac za dyskusje i zyczyc dalsych ciekwaych dyskusji
A jednak problem polega w zbyt małej wiedzy o egzaminie. Egzaminator z polskiego sprawdza całą pracę i widzi całą przyznaną przez siebie punkcję.Jest więc podatny na ludzkie odruchy (np. choć pisał pracę kretyn, to nie będę mu łamał życia itp.). Egzaminator z matematyki NIE ZNA punktacji za zadania sprawdzane maszynowo, bowiem te są sprawdzane dopiero PO ocenie części otwartych zadań przez człowieka. Czyli egzaminator nie wie, jak zdający napisał część zadań, a więc nie jest obciążony tą wiedzą. Co oczywiście zwalnia go z dywagacji, którym oddają się poloniści. Ot tyle … I jeszcze jedno, nikt tego nie wymyślił, aby bardziej „obiektywizować” matematykę. Jest to nacisk okoliczności (sposobu sprawdzania, skanowania kart odpowiedzi i in.)
@Endo
Tego się spodziewałem.
Wnioski są takie:
1) Oceny zadań z polskiego są uznaniowe, bo „chcący” egzaminator praktycznie w prawie każdej pracy na 19 czy 20 punktów gdzieś potrafi wygrzebać jeden czy dwa dodatkowe punkty i przepchnąć delikwenta.
2) Wobec istnienia psychologicznej motywacji, oceniający robią użytek z tej możliwości, czyniąc egzamin niesprawiedliwym.
3) Ponieważ efektu nie widać w matematyce, więc ten dwustopniowy mechanizm tam nie działa. Wiemy już, że sprawdzający są pozbawieni psychologicznej motywacji. Na podstawie dyskutowanych tu danych nie da się ustalić, czy oceny z matematyki też są uznaniowe i z każdej słabej pracy dają się wycisnąć dodatkowe punkty, czy nie.
4) Pozostaje to samo rozwiązanie pozbawiające motywacji wprowadzić do egzaminu z polskiego: podzielić arkusz na dwie części i dać do sprawdzenia dwóm nie kontaktującym się osobom, a potem tylko automatycznie sumować punkty. Będzie bardziej uczciwie.
5) Godny uwagi pozostaje kształt wykresu dla języka polskiego, odpowiadający krzywej Gaussa. W matematyce jest tak, że jak ktoś nie wie jakiejś podstawowej rzeczy, to ten brak odbija się w wielu miejscach. Na przykład braki w umiejętności algebraicznego przekształcania wzorów moga wyjść i w zadaniu o wielomianach, i w zadaniu z geometrii, i w zadaniu na granice ciągów. Zatem wyniki zadań nie są niezależne statystycznie. W polskim wykres wygląda tak, jakby wyniki poszczególnych zadań były statystycznie niezależne.
Właśnie ten dzwon i niedzwon budzą moje wątpliwości. W języku polskim (jako przedmiocie szkolnym) w istocie ktoś może świetnie znać zawiłości składni i jednocześnie nie znać lektur lub odwrotnie. Wyniki kogoś takiego pewnie będą właśnie trafiać do szczytu dzwonu. Skoro zaś w matematyce wszystko wynika z wszystkiego, to w sumie taki test powinien dawać wyniki bimodalne – szczyt blisko zera i szczyt blisko maksimum, a przeciętniaków powinno nie być. Ponadto, jeżeli rzeczywiście ten test z polskiego to suma sprawdzenia różnych umiejętności i wiedz niespecjalnie wzajemnie powiązanych, a test z matematyki to sprawdzenie tego, czy ktoś po prostu umie matematykę jako system, czy nie, to wtedy duża liczba zadań jest zbędna. Wystarczyłoby zgoła jedno, a inne tylko powielają sprawdzanie tej samej ogólnej umiejętności.
@J.Ty
A jednak nadal problem leży w zbyt małej wiedzy o egzaminie.
Pozwolę sobie na refleksję osobistą – wszędzie tam, gdzie pracują ludzie, wkrada się czynnik subiektywizmu. Przenosząc to na grunt egzaminu, to nauczyciel-egzaminator decyduje o tym, czy zdający wypełnił normę jakościową zaliczenia. Oczywiście podejmowane są próby zwiększenia obiektywizmu (np. anonimizacja prac, deregionalizacja, szkolenie egzaminatorów pod kątem umiejętności sprawdzania, wymogi formalne wykształcenia i stażu). Natomiast tylko maszyny nie ulegają emocjom.
Istnieje jeszcze jeden sposób, o którym piszesz. Wielokrotne (co najmniej dwukrotne) sprawdzanie przez różnych egzaminatorów. Niestety, w naszym kraju niemożliwe, z powodów różnych, np. bo świadectwa maturalne muszą być być wydane do końca czerwca. Od lat postulowane jest wydłużenie prac nad sprawdzaniem do końca sierpnia, i wydawanie świadectw we wrześniu. Bez powodzenia. Okazuje się, że głównym oponentem są wyższe uczelnie, które domagają sie od zdających świadectw na początku lipca, aby zamknąć rekrutację i mieć zasłużone wakacje. Sądzę, że problem jest o wiele poważniejszy, ale to jakby na inną dyskusję
Autorem obserwacji jest Przemysław Biecek ze SmarterPoland/UW, który jako pierwszy znalazł i przedyskutował te wykresy. Oczywiście autor demota nie musi podawać bibliografii, ale od Szalonych oczekiwałbym nieco więcej wiedzy.
http://smarterpoland.pl/index.php/2013/03/czy-polonisci-sa-mniej-obiektywni-a-matematyki-jest-za-malo-w-liceum/
@ Panek
Ale można mieć różną zdolność syntezy informacji i jej różnicowaniu służy wiele zadań
@Marcin Zaród
Niewątpliwie moja wina.
Z tą wiedzą to trochę przesada, to nie moja dziedzina, więc mogłem nie czytać. I nie czytałem.
Natomiast powinienem był poszukać, czy to już nie wypłynęło, ale nie zrobiłem tego. Przykro mi bardzo.
Mam wrażenie, że to co różni ocenę prac z j. polskiego od oceny z matematyki to metodologia oceniania. Pracę z j. polskiego ocenia się według pewnych kryteriów ale z dużym obciążeniem preferencji oceniającego. Przynajmniej część tej pracy. Natomiast pracę z matematyki się nie tyle ocenia co „mierzy” i wynik pomiaru jest nieomal obiektywny.
Z poważaniem W.
@ Wojtek 1942
To nie jest tak. Nie chce wchodzić w szczegóły, ale istnieją dwie metody oceniania pracy zdajacego – metoda holistyczna i analityczna. Obie maja swoje zalety i wady. Pierwsza to najogólniej rzecz biorąc całościowo spojrzenie na pracę, druga to krok po kroku śledzenie podanych przez zdajacego informacji. Jak widać , są one całkowicie rożne i przynoszą rożne efekty.
Co do rozkładu z matematyki, to widać wyraźnie, ze jest dwumodalny. Wynika to z powszechnosci egzaminu, w którym kompletne nogi zdają razem z orłami. Dla około połowy populacji wyniki są przesunięte w lewą stronę, czyli egzamin jest trudny, a dla części (około 1/4) wyniki są przesunięte w prawo. Stad dwumodalnosc. Ale ciekawych spostrzeżeń jest dużo wiecej. Niestety, mało kogo to interesuje
Z pewnością ocenianie prac maturalnych z języka polskiego jest bardzo uznaniowe jednak są elementy, które można w miarę sprawiedliwie ocenić. Moim zdaniem jednak jakieś chociaż minimlane wymogi powinny być stawiane. Nie mówię o inerpretowaniu wierszy ale swoje myśli na papier powinien umiec każdy Polak.
Marcin Zaród 22 kwietnia o godz. 13:48
„Autorem obserwacji jest Przemysław Biecek ze SmarterPoland/UW, który jako pierwszy znalazł i przedyskutował te wykresy. Oczywiście autor demota nie musi podawać bibliografii, ale od Szalonych oczekiwałbym nieco więcej wiedzy.”
Hm, z tą ilością wiedzy to czasami różnie bywa…nie zawsze wiadomo, jak ją mierzyć i czy sądy wydawać z aż taką surowością…
W listopadzie 2012 roku napisałem na Belferblogu:
**http://chetkowski.blog.polityka.pl/2012/10/26/uwierz-w-ucznia/#comment-105609
i nieskromnie wydaje mi się, że kto jak kto, ale pan Marcin Zaród powinien był o tym wiedzieć, gdyż, śmieszna sprawa, ale popełnił on swój wpis na tym samym blogu, kilka wpisów dalej:
**http://chetkowski.blog.polityka.pl/2012/10/26/uwierz-w-ucznia/#comment-105737
Moją winą było nie załączenie obrazka. Żyjemy w kulturze obrazkowej i prawdziwie ten ma wiedzę, kto daje obrazki.
Nie był to mój pierwszy wpis na Belferblogu na ten temat i nie był też ostatni. Tematem wyglądu histogramu wyników matur z różnych przedmiotów próbowałem też wcześniej zainteresować redakcje różnych czasopism, ale niestety bez powodzenia. Nie próbowałem uderzać do gazet z kręgu PiSu, gdyż nie chciałem dawać im dodatkowej amunicji do oskarżeń.
Ostatnim moim wpisem na Belferblogu na ten temat był poniższy:
**http://chetkowski.blog.polityka.pl/2013/03/07/stan-wzmozonej-maturalnosci/#comment-133977
czyli na tydzień przed wpisem pana Przemysława Biecka na jego blogu.
W roku 2009 a więc gdy po raz pierwszy zainteresowałem się histogramem wyników egzaminu maturalnego z języka polskiego na poziomie podstawowym, najbardziej zafrapowało mnie wystepowanie owej anomalii w okolicy progu zdawalności. Otóż porównanie histogramów z innych przedmiotów szybko pozwoliło mi dowiedziec się, że w 2009 istnienie owej anomalii (zjawiska przepychania słabych uczniów) było bardzo powszechne i dotyczyło prawie wszystkich przedmiotów oraz występowało także na poziomie rozszerzonym. Matematyka, na obu poziomach, też na nie wtedy cierpiała.
Ciekawa sprawa, ale z biegiem lat owo przepychanie zostało wyeliminowane właściwie ze wszystkich – poza językiem polskim (podstawa), przedmiotów. Biorąc pod uwagę skalę zjawiska (pole „wyrwy w wykresie”) – zdecydowanie język polski, podstawa bardzo się wyróżnia.
Wszystkie wykresy rozkładów dla każdego przedmiotu i dla obu poziomów z lat 2009-2012 zgrupowałem na slajdach Power Pointa w taki sposób, aby skale były takie same. Wtedy wszystkie punkty odcięcia (progi zdawalności) pięknie się ustawiają „pod linijkę” i nasze anomalie rzucają się w oczy. A także widoczne stają się wszelkie i bardzo ciekawe zmiany kształtów oraz wycentrowania samych krzywych rozkładów wyników. Nie jest tak, że z danego przedmiotu „natura rozkładu” pozostaje stała w czasie, o nie! Jest to zauważalne dla obu poziomów egzaminu maturalnego.
Dla roku 2011, język polski, podstawa spróbowałem oszacować pole pod wykresem w miejscu anomalii. Założyłem, że lewa strona wykresu (krawędź zbocza krzywej dzwonowej) powinna być symetryczna wobec krawędzi prawej. Sprawdziłem, czy wyniki ponad krzywą (pole pod wykresem, punkty 21-24) dla uczniów „ledwo co przepchniętych” jest równe polu uczniów, którzy powinni byli nie zdać (pole pod krzywą, punkty 17-20).
Policzyłem, jakiej liczbie uczniów (dla każdej z „przepychanych” liczby punktów 17-20) odpowiada pole anomalii i jaki jest to procent wszystkich zdających. Otóż pomaga się prawie 10 tysiącom maturzystów, co stanowi blisko 3% zdających.
Oczywiście można by powiedzieć, że to są niewielkie liczby, ale nasza waadza kochana jest co roku bardzo dumna z wysokiego i gromko ogłaszanego „odsetka sukcesów”. Który to odsetek wygląda następująco:
2009 – 94%
2010 – 95%
2011 – 96%
2012 – 97%
Zadanie dla szalonych naukowców; w którym roku osiągniemy 100% zdawalność? 😉
I właśnie w kontekście „zdawalności” wyeliminowanie 3% „przepychania z polaka” pogorszyło by wyniki o ho, ho, ho a może i więcej i „cofnęło nas” o całe trzy lata!
Jak kto jest zainteresowany to polecam przyjrzenie się zmianom w czasie histogramów dla różnych przedmiotów i poziomów.
Takie „drobnostki” jak to, że polski, matematyka i angielski to około 300 tys. zdających a niektóre inne przedmioty to tylko po parę, paręnaście tysięcy, że poziom nauki różni się bardzo pomiędzy szkołami oraz typami szkół, szczególy techniczne procesu tzw. „kalibracji matury” czy samego sprawdzania matur tylko mnożą możliwe kierunki analizy.
no, panie gospodarzu, jest pan pewnie w podobnej sytuacji jak vespucci, amerigo 😉
inne pytanie:
banowac czy to cos pomoze?
W przypadku egzaminu testowego błędem jest ustalanie z góry granicznych wartości uzyskanych punktów. To nie tylko umożliwia sprawdzającym „korektę” prac tuż poniżej minimalnego progu ale także powoduje, że oceny z różnych lat nie są równoważne – bo trudność pytań może być różna.
Nauczyciele powinni oceniać testy wiedząc jedynie, że np. percentyl 10 to dolna granica dostatecznego, percentyl 50 to dobry, percentyl 90 bardzo dobry (czyli 10% najgorszych prac dostaje gałę, kolejne 40% trójkę, następne 40% czwórkę i 10% najlepszych dostaje piątkę).
Ilość punktów odpowiadających poszczególnym percentylom (i stopniom) byłaby obliczana po sprawdzeniu wszystkich prac. Czyli po sprawdzeniu prac najpierw maturzyści dowiadywaliby się, ile zdobyli punktów. Jaka to jest ocena ogłaszano by po kilku dniach, kiedy podsumowano wszystkie wyniki.
Wątpię, że to, co teraz napiszę jest rzeczywistą motywacją osób, które konstruują egzaminy, ale przyzwyczaiłem się do stawiania nawet mało prawdopodobnych hipotez. Mianowicie:
1) Matura z tego przedmiotu musi być, jak z każdego innego, więc jest.
2) Kogoś tam da się odsiać (jeżeli nie ma instynktu zachowawczego i przy okazji jest b. głupi, to nie zda z powodu „błędu rzeczowego” w pracy pisemnej).
3) Reszty nie ma sensu odsiewać, bo wiedza, która powinna być sprawdzona po poziomie podstawowym dotyczy de facto tylko ścisłowców (bo każdy humanista i tak zdaje rozszerzenie i uczenie wyższe patrzą głównie na nie), którzy dobrze by było, żeby umieli poprawnie pisać i znali lektury (tego drugiego oczywiście nie sprawdzimy, bo istnieje taki wynalazek jak bryk, który wypadałoby przed maturą przeczytać).
Zatem, skoro wiemy, że takie narzędzie, jak matura podstawowa z polskiego niewiele zmienia, to zróbmy jakąś ściemę, która teoretycznie odsiewa tyle, ile trzeba, ale dobrze wiemy, że tak nie jest. „Klejmy durnia” jednym słowem.
Co matura właściwie powinna sprawdzać?
Zapomniałem podziękować. Dzięki temu wpisowi dowiedziałem się o istnieniu bloga Demotywatory.
Wstawić smiely czy nie wstawić? Teraz już nie wiem…