Penrose. Podziwiam, nie polecam

24 września 2022
Blog szalonych naukowców

Czytam właśnie książkę wybitnego fizyka Rogera Penrose’a „Moda, wiara i fantazja w nowej fizyce Wszechświata”, i choć jest bardzo ciekawa, trudno mi ją polecić szerszemu gronu odbiorców.

Penrose jest bez wątpienia fizykiem wybitnym. Geniuszem, noblistą znanym z tzw. twierdzenia o osobliwościach opublikowanego ze sławnym Stephenem Hawkingiem. Jednak popularyzatorem nauki pozostaje w moim odczuciu nie najlepszym.

Wspomniana książka jest bardzo ciekawa i dość kontrowersyjna, zadaje kłam popularnym obecnie teoriom fizycznym. Krytykuje teorię strun, obowiązującą interpretację mechaniki kwantowej, wreszcie inflację kosmiczną. Prezentuje ważne argumenty w ciekawy sposób, niemniej dość ciężko się to czyta. Mam wrażenie, że autor nie do końca się zdecydował, dla kogo pisze.

Każdy wykładowca wie, że sposób przekazywania informacji należy uzależnić od odbiorcy. Inaczej rozmawia się z kolegą specjalistą, inaczej ze studentem, jeszcze inaczej z zainteresowanym laikiem czy wręcz dzieckiem.

Tutaj właśnie mam z Penrose’m problem. Fizyk matematyczny, z wykształcenia matematyk, pisze bardzo nierówno. Raz przeraża bardzo zaawansowaną matematyką, kiedy indziej unika rzeczy stosunkowo prostych.

Kilka razy powtarza, że dla ułatwienia nie będzie poruszać pochodnych. Co prawda na pochodnych opiera się prawie cała dzisiejsza fizyka, ale Penrose ma litość dla czytelnika. I zaraz potem omawia wiązki.

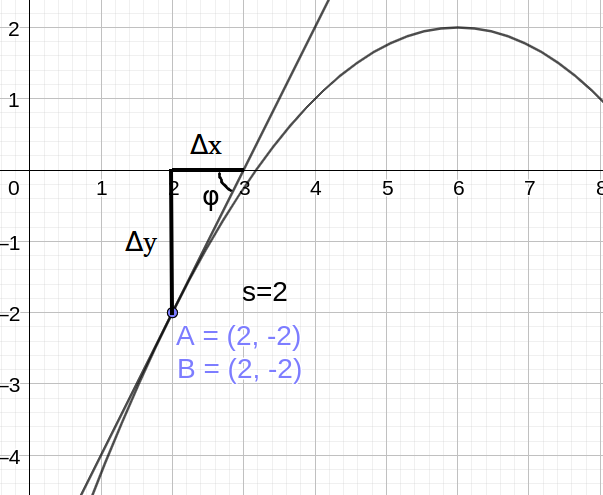
Co w tym dziwnego? Pojęcie pochodnej powinien zrozumieć każdy licealista z mat-fizu. Cóż to za dziwo – ta pochodna? Weźmy pewną funkcję na płaszczyźnie kartezjańskiej y=f(x). Teraz weźmy pewien punkt P z wykresu tej funkcji i zastanówmy się, jak szybko w tym punkcie funkcja rośnie lub maleje. Przykładowo: jeśli wykres obrazuje zmianę drogi względem czasu, pytamy o chwilową prędkość. A więc startując od punktu P, bierzemy pewien niewielki odcinek Δx, patrzymy, o ile na tym odcinku wzrosła (bądź zmalała) funkcja f (Δf) i dzielimy drugie przez pierwsze (patrz grafika powyżej). Jeśli weźmiemy wystarczająco małe Δx (matematycy oznaczają je przez dx, gdzie d to taka nieskończenie mała Δ), to otrzymany iloraz będzie dowolnie bliski rzeczywistemu tempu wzrostu funkcji. Graficznie możemy w tym punkcie wykreślić prostą dotykającą wykresu funkcji w tym właśnie punkcie, ale jej nie przecinającą (tzw. styczną). Jak pamiętamy ze szkoły, będzie ona prostą o wzorze ax + b. Występujące w tym wzorze a to właśnie pochodna naszej funkcji f w tym punkcie. Nową funkcję f’, która dla każdego x przyporządkowuje wartość pochodnej f w tym punkcie, nazywamy pochodną tejże funkcji. Oznaczamy ją też jako f’(x) = df/dx.

Trudne? Niekoniecznie. Weźmy funkcję liniową f(x) = ax + b. Styczna będzie w każdym punkcie identyczna z wyjściową funkcją, wobec tego pochodna f’(x) wynosi dla każdego x tyle samo, a.

Weźmy inny przypadek. Funkcja wykładnicza a do potęgi x (f(x) = a^x) określa chociażby wzrost bakterii na szalce w początkowej fazie (czy rozprzestrzenianie się koronawirusa). Wzrost jest tutaj w każdym momencie wprost proporcjonalny do liczby np. bakterii w tej chwili. A więc f’(x) = f(x) razy pewna stała c. Od czego może zależeć c? Od podstawy a. Ale czy w takim razie można wybrać taką podstawę a, by nasza stała c była równa 1 i by można było ją z równania wywalić? Pewnie. Wynosi między 2 a 3 i jest liczbą niewymierną (i niealgebraiczną, tzn. nie jest rozwiązaniem żadnego równania wielomianowego o współczynnikach wymiernych). Hm, nie idzie jej inaczej prosto zapisać, więc trzeba by ją jakoś nazwać… Macie jakiś pomysł? Jak by ją nazwać? Yyyy… eee…

Y kojarzy się z równaniami, więc lepiej nie, ale e może zostać. A więc funkcja f(x) = e^x jest równa własnej pochodnej. (No dobrze, oznaczenie e wybrano, bo kojarzy się z wielkim matematykiem Eulerem. Jest to ta sama liczba, którą matematycy definiują często w podręcznikach jako granicę (1+1/n)^n, gdy n zmierza do nieskończoności. Każdy ma swoje dziwactwa).

To teraz utrudnienie: licząc pochodną funkcji złożonej g(f(x)), mnożymy pochodną g przez pochodną f. Dlaczego? Pochodna funkcji złożonej dg/dx = dg/df * df/dx.

Po tym krótkim wprowadzeniu te straszne pochodne funkcji falowej psi z równania Schroedingera możemy sobie policzyć w pamięci. Mamy tam kilka razy e do coś tam razy x, a więc pochodna funkcji złożonej okazuje się iloczynem wyjściowej funkcji (pochodna e do coś tam x równa wyjściowej funkcji) razy stała coś tam (pochodna samej coś tam razy x).

Po ominięciu tego jakże trudnego zagadnienia Penrose wprowadza czytelnika w pojęcie wiązek. Co to ta wiązka? Struktura algebraiczna (chyba, rozumiem to dosyć słabo) powstała z przyporządkowania każdemu punktowi bazy identycznego włókna. Co to ta baza? Pewnie coś w stylu bazy przestrzeni wektorowej, będącej z kolei pewnym połączeniem grupy z ciałem (matematycy mówią „nad ciałem”) poprzez wprowadzenie operacji mnożenia o danych właściwościach. Jedno z nich, baza czy włókno, już nie pamiętam, musi być rozmaitością.

Rozmaitość to struktura, której w każdym punkcie w dowolnie małym otoczeniu nie można odróżnić od pewnej przestrzeni Euklidesa. Na przykład okrąg w dużym powiększeniu przypomina prosta, powierzchnia Ziemi – płaszczyznę (pozdrawiamy zwolenników płaskiej Ziemi), jaka jest geometria naszego Wszechświata, nie ustalono.

Zrozumiałem to tak, że każdemu punktowi przestrzeni przypisujemy pewną strukturę algebraiczną, opisującą np. pole wektorowe czy dodatkowe wymiary przestrzenne. Prościej wytłumaczyć nie potrafię (i zaręczam, że Penrose’owi też się nie udaje. Gdybym nie znał wcześniej jako tako algebry, nie zrozumiałbym z tego kompletnie nic).

Penrose argumentuje w ten sposób choćby przeciwko wielowymiarowej teorii strun. Podaje, że gadanie o 26 wymiarach czasoprzestrzennych to zwykłe wciskanie kitu, nawet jeśli kit elegancko określamy rozmaitościami Calabiego-Yau. Wskazuje, że takie ukryte wymiary musiałyby wpływać na obserwowane przez nas cechy świata, a nikt ich nigdy nie widział. Co akurat można zrozumieć bez dziwacznych struktur algebraicznych znacząco wykraczających poza matematykę licealną.

Dalej jest jeszcze gorzej. Spinory, twistory… Co to takiego? Mnie się to w głowie nie mieści, niech to Państwu Penrose tłumaczy…

Marcin Nowak

Bibliografia:

  • Penrose R: Moda, Wiara I Fantazja w nowej fizyce Wszechświata. Copernicus Center Press, Kraków 2020

Ilustracja: Yomomo, za Wikimedia Commons, CC BY-SA 4.0