Czego w szkole (nie) uczyli

27 sierpnia 2022
Blog szalonych naukowców

W pewnym sondażu znalazłem ostatnio pytanie: „Czy uważasz, że istnieją dwie płcie?”. Zastanawiałem się, co bym odpowiedział, i właściwie nie wiem. To jedno z tych pytań, w przypadku których odpowiedź zależy od kontekstu. Istnieje prosta odpowiedź, zgodna z tym, czego uczą w szkole, ale na studiach już uznana nie zostanie. Jeśli dobrze poszukać, takich szkolnych uproszczeń znajdzie się mnóstwo. Nie żeby ktoś celowo chciał ideologizować czy zakłamywać rzeczywistość. Po prostu jest ona skomplikowana. Ale daje się łatwo opisać w przybliżeniu. Rozpatrzmy kilka przykładów z różnych przedmiotów.

Matematyka – suma kątów w trójkącie

Trójkąt w geometrii sferycznej

Suma kątów w trójkącie równa się 180 st. – uczą w podstawówce. Niektórzy matematycy dręczą nawet uczniów konstrukcyjnym dodawaniem do siebie kątów w trójkącie, by im to unaocznić. Prawdy matematyczne są wieczne i niezmienne, Platon zawyłby z uciechy…

No dobrze, ale z geometrii bardzo często korzystamy, licząc odległości i powierzchnie na Ziemi. Możemy wytyczyć trójkąt na mapie. Rozpatrzmy więc następujący. Umieśćmy wierzchołek A na biegunie północnym. Oba ramiona niech idą wzdłuż południków. Weźmy teraz dowolny równoleżnik – przecina oba południki pod kątem prostym. Ile wynosi suma kątów w trójkącie? 2 razy 90 stopni + kąt między południkami… Okaże się, że kąty sumują się do 180 st. tylko na płaszczyźnie, gdzie obowiązuje piąty aksjomat Euklidesa. W innych geometriach tak nie jest.

Fizyka – elektrony na orbitach

Rozkłady prawdopodobieństwa ośmiu stanów stacjonarnych wodoru atomowego wzdłuż osi y

Pamiętamy ze szkoły obraz atomu, w którym masywne jądro z protonów (czerwone piłeczki) i neutronów (niebieskie piłeczki) okrążają po orbitach elektrony (żółte piłeczki). Taki miniaturowy układ planetarny.

Tylko że elektrony mają ładunek, a poruszający się z przyspieszeniem (a więc także kręcący się po okręgu) ładunek wywołuje zmiany w polu elektrycznym. Przez to emituje energię, a więc musi ją tracić. To prowadziłoby do widowiskowego rąbnięcia w jądro. Wedle klasycznej fizyki czas życia atomu wynosiłby ułamek sekundy. Model Bohra nakłada na to kilka łat, wedle których elektron na swojej orbicie nic nie wypromieniowuje i nie może jej tak po prostu opuścić. Bo? Bo inaczej nam się wali system.

Obecnie nie opisuje się elektronu jako żadnej piłeczki ani nawet obiektu zajmującego jakiekolwiek konkretne miejsce (byłoby to wbrew zasadzie nieoznaczoności Heisenberga). Elektron opisuje tzw. funkcja falowa (w tym wypadku zwana orbitalem). Teraz weźmy fragment przestrzeni. Dla każdego z tworzących go punktów sumujemy kwadrat modułu tejże funkcji. Moduł danej liczby to odległość od 0. Ale po co ten moduł, czy kwadrat modułu nie jest z definicji równy kwadratowi danej liczby? Nie, to zachodzi tylko dla liczb rzeczywistych. A są inne (w tym wypadku zespolone), o tym też w szkole nie uczyli. Po obliczeniu sumy kwadratów modułów wszystkich nieskończenie wielu punktów (czyli scałkowaniu po danym fragmencie przestrzeni) wychodzi nam prawdopodobieństwo, że elektron znajduje się w tym obszarze. Prawdopodobieństwo, że elektron atomu wodoru znajduje się dokładnie na orbicie Bohra, wynosi dokładnie 0.

Chemia – elektrony tlenu

Budowy cząsteczek uczy się w liceach na podstawie wzorów Lewisa – wokół symbolu atomu przedstawia się jego elektrony walencyjne i łączy je kreskami wyobrażającymi sparowanie. Rozważmy dwuatomową cząsteczkę tlenu O2. Wzór jest bardzo prosty:

|O = O|

Tylko że badania w polu magnetycznym wskazują na obecność dwóch niesparowanych elektronów w cząsteczce. Czyżby więc wiązanie było pojedyncze:

|O. – .O|

Spektroskopia ewidentnie potwierdza obecność wiązania podwójnego (wiązanie takie jest krótsze i silniejsze niż pojedyncze).

Jak widać, wzory Lewisa mają znaczne ograniczenia i niektórych cząsteczek po prostu nie da się za ich pomocą przedstawić. Jeśli atomy zbliżą się do siebie, na nakładających się obszarach o wysokim prawdopodobieństwie znalezienia elektronu funkcje falowe się dodaje. Ale z dodania dwóch orbitali dwóch atomów powstają też dwie orbitale cząsteczkowe: o niskiej energii (wiążący) i o wysokiej (antywiążący). Liczba wiązań to różnica liczb elektronów na orbitalach wiążących i antywiążących podzielona przez dwa. Można to przedstawić na rysunku, dość dalekim od wzoru Lewisa.

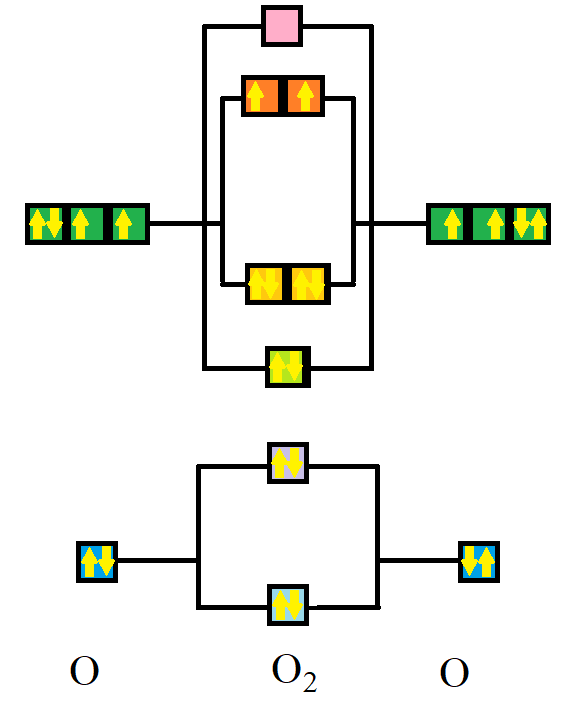
Orbitale cząsteczki tlenu pośrodku, orbitale swobodnych atomów po bokach. Elektrony jako strzałki. Wysokość na rysunku odpowiada energii orbitali, orbitale cząsteczkowe o energii niższej niż wyjściowe orbitale atomowe są wiążące, te o wyższej antywiążące.

Biologia – wyginięcie dinozaurów

Dinozaury stanowią w języku popularnym niekiedy wręcz synonim czegoś dawnego, nieprzystosowanego do nowych warunków, co musiało odejść i wymarło. Zniknęły 65 mln lat temu wskutek uderzenia asteroidy, każde dziecko to wie.

Tylko że… popatrzmy na definicje. Obecnie w paleontologii (nauce o dawnym życiu) system rangowy Linneusza, którym lubią jeszcze dręczyć w szkołach, pęka w szwach. Taksony (grupy organizmów) rozumie się kladystycznie. Klad to grupa pochodząca od wspólnego przodka. Definiuje się go często przez wskazanie, że chodzi o ostatniego wspólnego przodka tych dwóch gatunków czy, rzadziej, grup. Dinozaury definiuje się formalnie różnie, ale wszystkie definicje oznaczają dokładnie tę samą grupę zwierząt. Przykładowo definicja „tyranozaur + triceratops” oznacza potomków ostatniego wspólnego przodka tyranozaura i triceratopsa.

Udowodniono także, że ptaki pochodzą od dinozaurów drapieżnych. Żaden niespecjalista nie odróżni szczątków zaawansowanego ewolucyjnie bliskiego ptakom dinozaura od jego bliskiego krewnego, pierwotnego ptaka. A teraz zastosujmy definicję dinozaurów. Ptaki są znacznie bliższymi krewnymi tyranozaura niż triceratops. Ergo: pochodzą od ostatniego wspólnego przodka tyranozaura i triceratopsa. Co oznacza, że są dinozaurami. Trochę głupio mówić, że wyginęła grupa zwierząt licząca dziś grubo ponad 10 tys. gatunków.

Citipati, dinozaur drapieżny z grupy owiraptorozaurów

Itd. Itp. Takich uproszczeń przekazywanych w szkołach jest mnóstwo. To nie zarzut, przeciwnie – program i tak jest przeładowany, a współczesnej wiedzy naukowej często po prostu nie można przedstawić bez uproszczeń w sposób zrozumiały dla ucznia czy nawet przeciętnego dorosłego odbiorcy. Z drugiej strony – ma to dość ważne konsekwencje. W codziennym życiu zazwyczaj można polegać na wiedzy szkolnej. Jeśli pojawiają się jakieś trudności, niepewność, rozbieżność zdań, a zwłaszcza jeśli ktoś bardziej obeznany mówi coś innego – zawsze trzeba mieć na uwadze upraszczający charakter szkolnego nauczania. A w razie potrzeby – zdobyć więcej informacji bądź słuchać ekspertów.

Marcin Nowak

PS W sumie należy przyznać, że moje wyjaśnienia rozpatrywanych kwestii również były dość pobieżne i uproszczone.

Ilustracje:

  • Trójkąt na płaszczyźnie sferycznej, Mikue, za Wikimedia Commons, GNU 1.2
  • Rozkłady prawdopodobieństwa ośmiu stanów stacjonarnych wodoru atomowego wzdłuż osi y, Ulrich Mohrhoff, za Wikimedia Commons, CC BY-SA 3.0
  • Orbitale tlenu, rysunek wykonany przez autora
  • Citipati osmolskae, rekonstrukcja, PaleoNeolitic, za Wikimedia Commons, CC BY-SA 4.0