O czym milczy matematyka
Grzegorz w swoim jubileuszowym, dwusetnym tekście napisał o twierdzeniu Gödla o niezupełności. Podrążę ten temat w stronę kilkakrotnie poruszanego u nas tematu „co może wynikać z milczenia”.
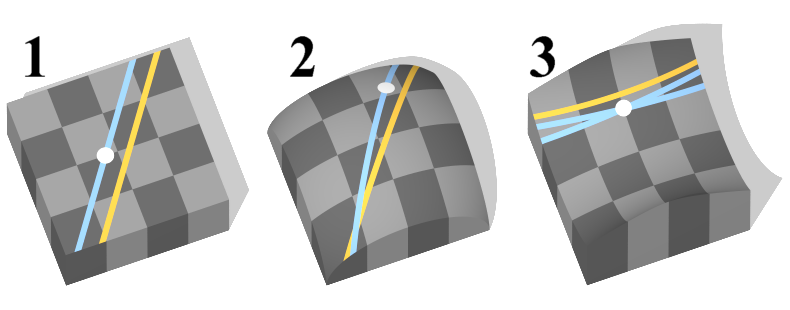
Zacznijmy jednak od czegoś starszego i nie mniej sławnego. Chodzi o postulat (albo aksjomat) Euklidesa o równoległych. Jest wiele jego sformułowań, zadowolę się takim:
Na płaszczyźnie, dla każdej prostej p i każdego punktu P leżącego poza p, istnieje dokładnie jedna prosta nie przecinająca się z p i przechodząca przez P.
Odkąd Euklides stworzył swój system aksjomatów geometrii, trwały próby wykazania, że aksjomat o równoległych wynika z pozostałych aksjomatów. Ostatecznie, w XIX wieku Nikołaj Łobaczewski i Janos Bolyai (byli też inni odkrywcy, ale te dwa nazwiska weszły do nazwy) wykazali, że nie wynika: można stworzyć zgodną z pozostałymi aksjomatami geometrię, w której przez P przechodzi nieskończenie wiele prostych nie przecinających się z p.
Jakiś czas później Bernhard Riemann stworzył kolejną zgodną z pozostałymi aksjomatami geometrię, w której dla odmiany przez P nie przechodzi żadna prosta nie przecinająca się z p.
Morał jest taki, że
Pozostałe aksjomaty Euklidesa milczą o tym, ile prostych nieprzecinających p przechodzi przez P.
Odkrycie Kurta Gödla można streścić tak:
Są zdania arytmetyki, o których jej aksjomaty milczą.
W odróżnieniu jednak od milczenia geometrii, milczenie arytmetyki jest dużo bardziej fundamentalne, bo żadne uzupełnianie zestawu aksjomatów nie pomaga. Gödel wykazał tak naprawdę, że każdy zestaw aksjomatów arytmetyki, jeśli tylko jest niesprzeczny i daje się opisać w skończony sposób, musi milczeć o czymś.
Niewątpliwie milczenie odkryte przez Gödla wiele nam mówi o ograniczeniu naszych możliwości poznawczych i skłania do pokory wobec matematyki, świata, który przecież powstał i żyje w naszych głowach.
Jerzy Tyszkiewicz
Ilustracja: Peo, Wikimedia Commons, CC BY-SA 3.0
Kwestia porządkowa. Po przygodach z moimi tekstami deklaruję co następuje:
Osoby komentujące w sposób obraźliwy dla innych bądź całkowicie nie na temat będę banował do zakończenia dyskusji pod tekstem. Mam nadzieję, że ten sposób wywodzący się ze sportu pozytywnie wpłynie na rozwagę w wyrażaniu swoich emocji. Swoich współautorów upoważniam do banowania, gdyby wcześniej ode mnie je zauważyli.

Komentarze
Dochodzi tu chyba jeszcze jeden rodzaj pokory. Niezupełność dotyczy nie tylko naszych możliwości poznawczych i narzędzi, ale również realnego świata (jeśli ktoś wierzy w niezależną od naszego postrzegania realność). Świat jest zatem niedopowiedziany i nie da się ująć w zamkniętą, zupełną i niesprzeczną strukturę. Mi się to podoba.
Ja bym to raczej ujął tak: niewątpliwie milczenie odkryte przez Gödla wiele nam mówi o ograniczeniu naszych możliwości poznawczych i skłaniać powinno matematyków do pokory wobec złożoności oraz niepoznawalności realnego świata, jako iż ich (matematyków) świat twierdzeń, dowodów oraz aksjomatów matematycznych jest przecież tylko sztucznym a mocno niedoskonałym modelem rzeczywistości, który to model przecież powstał i istnieje tylko w ich (matematyków) głowach.
Pozdrawiam.
I skąd bierze się wciąż to: BŁĄD: Could not read CAPTCHA token file?
Jeśli chodzi o błąd „Could not read CAPTCHA token file”, to chyba ta catpcha po pewnym czasie „traci ważność” i serwer o niej zapomina. Najlepiej zawsze kliknąc w znaczek przeładowania i dostać nowy, świeży obrazek.
Z pewnego wpisu na G+/pewne dyskusji:
„W internecie można znaleźć niezwykłe rzeczy. Ostatnio czytałem o listach ( http://www.math.uwaterloo.ca/~snburris/htdocs/noneucl.pdf ) jakie wymieniali między sobą Gauss i Bolyai ( ojciec i syn). Farcas Bolyai i Gauss byli bardzo dobrymi przyjaciółmi. W jednym z listów jakie wymienili, w okolicach 1800 roku, Bolyai oznajmia Gaussowi że zamierza „osadzić geometrię Euklidesa na solidnych podstawach co między innymi ma polegać na przeprowadzeniu dowodu V pewnika. Następnie następują 32 lata przerwy w korespondencji. Bolyai w ich trakcie stara sie bezskutecznie dokonać tego co obiecał, aż popada w zniechęcenie. Farcas sądzi że zmarnował swoje życie, próbując dowieść V pewnik geometrii Euklidesa. Swojemu synowi, Janosowi, który miał ciągoty matematyczne, zakazał zajmować się tym zagadnieniem. Bolyai syn zlekceważył ostrzeżenie, i pracował nad tymi samymi zagadnieniami kontynuując pracę ojca. W końcu doszedł do rewolucyjnego wniosku że nie da sie udowodnić V pewnika, a jako dowód tego odkrycia, skonstruował niesprzeczną geometrię w której V pewnik był nieprawdziwy. Janos Bolyai, syn, napisał wtedy do Gaussa list w którym przedstawiał mu swoje koncepcje na temat. Było to w 1831 roku. List ów nie doczekał sie odpowiedzi, a ważna część korespondencji, zaginęła. Wobec takiego obrotu spraw Farcas Bolyai, ojciec, napsiał do Gaussa list, w 1832 roku, z prośbą by ten odpowiedział na list syna Janosa, zaś wraz z tym listem przesłał brakujace materiały. Gauss odpowiedział na list Farkasa Bolyai, po trwającym 32 lata braku kontaktu, twierdząc że pomysł jego syna jest sensowny, ale że nie Janosowi należy się pierwszeństwo ale jemu, Gaussowi, bowiem sam wykonał całkiem podobne dowody i rozumowania.”
Reszta ( niezwiązana bezpośrednio z tematem geometrii nieeuklidesowych) tu: http://fiksacie.wordpress.com/2013/02/04/po-co-komu-taka-plwikipedia/
?
a moze jest tak, ze potrzebujemy nowy aksjomat (-y) i matematycznych zwyklych aksjomatow nie mozna uzyc jako przeciwdowodow. Istniejace przekonanie o hipotezie – continuum powinno byc uznane za falszywe.
@J.Ty.
1. Tyle, że ja zawsze pobieram nowy kod przez wysłaniem komentarza, a więc jest to zapewne fundamentalny problem z oprogramowaniem tego blogu (gdybym podał „przestarzały” kod, to bym dostał informację o tym, że jest on już nieważny, a nie że system nie może go odczytać). Obawiam się więc, że jest to oprogramowanie dziełem wybitnych teoretyków, tyle że wyznających z gruntu rzeczy błędną teorię?
2. Generalnie ? słabość matematyki polega przede wszystkim na tym, że opiera się ona na aksjomatach (pewnikach, dogmatach etc.), a te są przecież z definicji nieudowadnialne, a więc nienaukowe. Tak więc, moim zdaniem, należy opracować od nowa podstawy nauk (na początek ścisłych) w taki sposób, aby wyeliminować z niej obecną matematykę, a co za tym idzie takie oczywiste nonsensy jak n.p. nieskończoności, które nawet z fizyki potrafiły ostatnio uczynić coś w rodzaju systemu wiary (n.p. ta żałosna wręcz wiara fizyków w tzw. inflację kosmiczną czy też takie, z gruntu rzeczy nienaukowe praktyki, jak n.p. tzw. renormalizacja). Niemożliwość zunifikowania mechaniki kwantowej z ogólną teorią względności, niemożliwość uzyskania reakcji termojądrowej z pozytywnym bilansem energetycznym oraz rozpaczliwe wręcz próby fizyków skonstruowania weryfikowalnej teorii superstrun (supermembran) są tu najlepszymi chyba przykładami na to, że fizyka, a wraz z nią praktycznie cała nauka, znalazła się dziś w ślepym zaułku, a to z powodu posługiwania się niepoprawnym narzędziem, jakim jest współcześnie uprawiana ortodoksyjna matematyka, która sprawdza się owszem w sklepie przy wydawaniu reszty ze stosunkowo małej kwoty pieniędzy, ale nie sprawdza się ona w skalach ekstremalnych, czyli w skali subatomowej oraz skali kosmicznej. A bez zrozumienia zjawisk zachodzących w tych ekstremalnych skalach nie ma przecież mowy o poznaniu, a tym bardziej już o zrozumieniu natury naszej rzeczywistości.
Pozdrawiam.
Z tą CAPTCHĄ jest też problem na niektórych innych blogach Polityki. Komunikat mówi, że nie może odczytać, również po kilkukrotnym odświeżeniu, a kiedy odświeżę całą stronę, powraca uparcie ten sam kod, którego nie można było odczytać za pierwszym razem. Również po otwarciu strony w nowym okienku pojawia się ten stary kod. Po kilku próbach odświeżenia – ni z tego ni z owego nowy kod zostaje zaakceptowany.
Pytam mój komputer – dlaczego?
Milczy.
Matematyka jest tylko językiem zapisu (stenotypicznym, jak twierdzi Alfred Marshall, twórca ekonomii matematycznej), na pewno nie jest narzędziem badawczym i nie pomaga w zrozumieniu świata. To, że czasem brak językowi wyrażeń, czy słów, jest dość oczywiste. Rozpoznanie świata powinno zaczynać się od myślenia i opisu w języku żywym, niehermetycznym.
A więc do pokory przed czymś, co jest w naszych głowach…
@Ekonom – „renormalizacja” – to że teoria strun jest nieweryfikowalna to prawda, podobnie jak fakt że fizyka teoretyczna przez zbytnią koncentrację na tym podejściu przeżywa obecnie kryzys. Jednak nie oznacza to że wszystkie rzeczy które Pan wypisał sa bzdurami czy nonsensami jak Pan twierdzi. Akurat renormalizacja to słowo pojemnik na wiele technik znajdywania punktów stałych i w kilku z nich mamy do czynienia z w miarę konsystentnym postępowaniem ( renormalizacja procedurą Koguta). Tym co czyni tą procedurę nieścisłą nie są niedostatki matematyczne, a raczej pewne założenia fizyczne, które niekoniecznie są oparte na pewnych podstawach.
Co do nieskończoności – zasadniczo nie ma z nimi wielkiego problemu gdyż są dosyć dobrze ( co nie znaczy że całkowicie) zrozumiana.
Rola aksjomatów jest całkowicie inna niż Pan pisze, a kwestia ich dowodzenia jest całkowicie jasna – np. w ramach aksjomatyki teorie zbiorów można dowodzić aksjomatów (pod)teorii wyrażanych w jej języku. Znacznie ciekawsze i mniej oczywiste rzeczy dzieją się na styku logiki 2-giego i wyższych rzędów, oraz teorii toposów, a juz szczególnie polecam zainteresowanie sie Univalent Foundations ( polecam linki znajdujące sie na dole mojego wpisu: http://fiksacie.wordpress.com/2012/01/05/dowod-troche-bardziej-skomplikowany-coq-cz-3/ oraz to co w międzyczasie wytworzono – np. 400 stronicowa rekonstrukcja matematyki w tym systemie )…
Nauka oderwana od matematyki… No ciekawe. Da się tak wyrazić coś, czego nie wiedziano w średniowieczu?
@mpn
Nie „nauka oderwana od matematyki”, ale nauka poszukująca lepszej matematyki, niż ta obecnie (a generalnie od czasów Newtona i Leibniza) używana, a która zapędziła fizykę w ślepy kąt, z którego jedyne wyjście jest przez jego porzucenie. Niestety, ale naukowcy zainwestowali za dużo swego czasu w tą obecnie znaną oraz wszędzie nauczaną matematykę, a więc nie mają oni odwagi jej porzucić, pomimo iż jest ona w oczywisty sposób błędna, jako iż nie sprawdza się ona w konfrontacji z fizyczną rzeczywistością.
@Kakaz
1. Renormalizacja jest tak samo naukowa jak jedność Trójcy Świętej. Teolodzy też są konsystentni w ich pseudonaukowych rozważaniach na temat istoty owej Trójcy Świętej. Poza tym, to w fizyce nie powinno się robić nieweryfikowalnych założeń, gdyż wtedy przestaje ona być nauką, a zaczyna ona być, jak n.p. teorie superstrun, rodzajem wiary czy też innego kultu parareligijnego.
2. Nieskończoność jest zaś pojęciem wewnętrznie sprzecznym, co najlepiej ilustruje choroba umysłowa jej ?wynalazcy?, czyli Cantora.
2. Aksjomatów się z definicji nie dowodzi, stąd też matematyka na nich oparta jest konstrukcją z definicji błędna, a jej błędy, wynikające z przyjmowania nieudowadnialnych aksjomatów, najlepiej widać w praktyce, czyli w tym, że ta współcześnie używana matematyka zapędziła fizykę w ślepą uliczkę niezgodnych ze sobą, a więc z definicji błędnych, dwóch prób opisu rzeczywistości, czyli niezgodnymi ze sobą teorii grawitacji (ogólnej teorii względności) oraz teorii pozostałych oddziaływań (mechaniki kwantowej) oraz w rozpaczliwej, a z góry przecież skazanej na niepowodzenie próby wytłumaczenia złożoności wszechświata poprzez wymyślanie z góry przecież nieweryfikowalnych pseudonaukowych hipotez typu ?superstrun?, albo też innych ?holograficznych? wyjaśnień. A jak wyniki badań nie zgadzają się z teorią, to się te wyniki ?nagina?, n.p. oznajmiając odkrycie ?boskich? cząsteczek albo tzw. fal grawitacyjnych. Tyle, że te ?boskie? cząsteczki oraz fale grawitacyjne istnieją tylko w komputerowych modelach, a komputery potrafią dziś tworzyć doskonałe trójwymiarowe, dynamiczne złudzenia ? patrz n.p. film Grawitacja.
A to wszystko by było tylko zabawą czy też hobby naukowców, gdyby nie to, że te zabawy kosztują podatników grube miliardy dolarów czy też innych euro. 🙁
@Meruńka
Nigdzie matematyka nie poniosła tak spektakularnej klęski jak w ekonomii. Modele ekonometryczne okazały się przecież całkowitą klęską, zarówno na poziomie mikro (n.p. giełda) jak też i na poziomie makro (modelowanie gospodarki narodowej).
@markot
Oprogramowanie tego blogu zostało wyraźnie napisane przez matematyków, czyli osoby nierozumiejące działania sieci komputerowych oraz niemające pojęcia o tym, jakiego ?interfejsu? chcą użytkownicy.
@kagan: „Nigdzie matematyka nie poniosła tak spektakularnej klęski jak w ekonomii. Modele ekonometryczne okazały się przecież całkowitą klęską, ”
Proponuje nie winic matematyki, a ekonomistow. Ekonomisci posluguja sie matematyka z maestria I efektywnoscia malpy uzbrojonej w brzytwe. Podobnie mozna by obwiniac garnki emaliowane z tego powodu ze w pewnej restauracji jedzenie jest do niczego.
Na dodatek, ekonomistom myla sie modele matematyczne z rzeczywistoscia I tak dalej
„Oprogramowanie tego blogu zostało wyraźnie napisane przez matematyków”
Matematycy nie pisuja oprogramwoania do blogow. To programisci pisza orpogramwoanie do blogow. Na ogol ci programisci sa tak sobie albo I nijako wyksztalceni w matematyce
@kagan: „pomimo iż jest ona w oczywisty sposób błędna, jako iż nie sprawdza się ona w konfrontacji z fizyczną rzeczywistością.”
Nie jest zadaniem I celem matematyki opisywanie czegokolwiek. Akurat tak sie zdarza, ze niektore rzeczy w matematyce nadaja sie do opisywania tego I owego, jednego lepiej, drugiego gorzej.
Jako specjalista od tworczosci Stanislawa Lema powinien Pan znac jego analogie o matematyce jako „szalonym krawcu”. Polecam
A matematyka sama w sobie nie jest bledna. Jest bledna wtedy gdy w dowodzie jest blad
Inna matematyka? No to jaka? Na czym oparta?
Pomimo że to trolowanie, to jednak odpowiem, bo uważam że @Kagan porusza interesujący i ważny, a często źle przedstawiany czy wręcz mylnie, element matematyki – ” Aksjomatów się z definicji nie dowodzi” – nic bardziej błędnego. Warto poczynić tu następujące uwagi:
1. jakże się „nie dowodzi” skoro cały wpis powyżej i korespondencja Gaussa z Bolyai ojcem poświęcona jest kwestii dowiedzenia V aksjomatu Euklidesa? Skoro „się nie dowodzi” dlaczego do czasu prac Bolyayi, Łobaczewskiego i Gaussa całe tabuny matematyków starały sie go dowieść? I dziś ludzie starają sie „dowodzić” że jakiś aksjomat, szczególnie bogatych teorii jest zależny lub nie od innych. Jest to absolutnie fundamentalna kwestia w wypadku każdej teorii. Chcąc zatem odczytać wpis Kagana w sposób pozytywny ( warto spróbować dla samego przedstawienia poglądu 😉 musimy uznać zatem że autorowi ine chodzi o praktykę uprawiania matematyki ( gdzie próby dowiedzenia aksjomatów, udowodnienia ich zależności lub niezależności od pozostałych, są POWSZECHNE by wymienić tylko wieloletnie starania zakończone dowodem Cohena i wynalezieniem metody forcingu, by dowieść że pewnik wyboru jest niezależny – a więc nie da sie dowieść – od aksjomatów ZF Teorii Mnogości, oraz by dowieść że hipoteza kontinuum także jest od nich niezależna – a zatem może być przyjęta za kolejny aksjomat https://en.wikipedia.org/wiki/Forcing_%28mathematics%29 ) ale o tzw. zasady.
2. czyli Kaganowi nie chodzi o to co robią ( zapewne w jego opinii głupi ) matematycy, bo ci aksjomaty starają sie dowieść, lub dowieść że się ich nie da dowieść, ale o tzw. zasady. Mianowicie zapewne kagan wyobraża sobie że to jest tak. Matematyk siada i na kartce pisze 5-7 aksjomatów, których nie będzie dowoził, a następnie tworzy z nich teorię. Nie wiem czy tak postępują matematycy, wszakże taka praktyka jest możliwa, dlaczego nie? Służą do takich zabaw całe systemy matematyki symbolicznej, jak Coq, a sa nawet i takie które na podstawie podanych aksjomatów starają sie generować, czysto kombinatorycznie, twierdzenia ( -> Doron Zeilberger na swojej stronie ma kilka generatorów twierdzeń napisanych w mathematica czy maple? Polecam jego książek „A = B”, dostępna w internetach, poświęconą po części takim zagadnieniom.). Zatem działanie takie jest możliwe. I tu dochodzimy do fundamentalnego rozróżnienia. Mamy bowiem do czynienia z pomieszaniem terminologii, czy pojęć, wynikającym zapewne z faktu że w szkole średniej nie uczą juz teraz logiki. Otóż systemy rozumowania dzielą sie na nieformalne i formalne. Systemy formalne to takie które posługują się językiem formalnym w którym ściśle określone sa wszystkie symbole, gramatyka itp. Systemy nieformalne to wszystkie te dla których językiem ich rozwijania jest mowa potoczna. OCZYWIŚCIE matematyka jest systemem nieformalnym. W przeszłości do wyjątkowej rzadkości należały książki jak te wydawane przez panią Helenę Rasiową (**), w których przebieg wykładu zbliża się ( ale nie jest!) do stanu systemu formalnego.
3. System formalny zas wymaga określenia języka. Język zawiera stałe ( jak znak równości, kwantyfikator ogólny itp.), symbole zmiennych ( które wiąże kwantyfikator np.) , atomowe symbole na oznaczanie relacji ( np. relacja „jest elementem” w teorii zbiorów itp.) oraz jakieś określenie własności tych symboli. Aby budować system formalny zwykle na dzień dobry zakładamy że obowiązują nas prawa logiki klasycznej, zwykle 1-szego rzędu. mamy zatem na starcie symbole, stałe, relacje i logikę 1-wszego rzędu. Same symbole to za mało by sie dobrze bawić, dlatego dodajemy do naszego systemu także reguły wnioskowania, bowiem nie każda „operacja” na zadanych symbolach jest równoprawna. Reguł wnioskowania, tzw. reguł inferencji, może być bardzo dużo, co znacząco może komplikować system. Elementarnym wymogiem wydaje się być by owe reguły prowadziły od zdań prawdziwych do zdań prawdziwych co oczywiście sie dowodzi, ale dlaczegóż ktoś nie miałby badać systemów sprzecznych? Można jak kto chce. Systemy określa sie tu dwojako. Jeśli system logiczny nie posiada aksjomatów, ale ma pewien zbiór reguł inferencji, mówimy o systemie dedukcyjnym. Systemy takie badał jako pierwszy Jaśkowski i Gentzen. Jeśli jako reguły inferencji ( nadal bez aksjomatów!) weźmiemy zasadniczo znane reguły logiki ( przykłady we wpisie: http://fiksacie.wordpress.com/2011/12/30/co-mi-sie-wydaje-ze-wiem-o-automatycznym-dowodzeniu-twierdzen-i-systemie-coq/ ) to system taki nazwiemy systemem dedukcji naturalnej. Trudno sie to bada bo jest wiele metod przekształcania napisów. Dlatego kiedy formalizujemy istniejące teorie, zwykle bierzemy jedną regułę inferencji – tylko modus poens. Dowody konstruuje się w takich strukturach przez podanie ciągu przekształceń od innych udowodnionych twierdzeń, do takiego którego dowodu szukamy gdzie po drodze wolno nam tylko ożywać reguł inferencji. Zapis takiego „przejścia” od jednych napisów do innych – nazywamy dowodem. Okazuje się, że tak długo jak mamy do czynienia z samą logiką klasyczną ( bez predykatów i dodatkowych aksjomatów), cały system jest rozstrzygalny i zupełny – to znaczy każde twierdzenie ma dowód, a wykonuje sie go na rozmaite sposoby, np. metoda tabelek 0-1-kowych. Dodanie do niego predykatów ( kwantyfikacja!) czyni system nierozstrzygalnym, jest on jednak nadal zupełny. Zupełność oznacza że każde zdanie w nim wyrażone jest albo prawdziwe albo fałszywe, zaś jeśli jest prawdziwe we wszystkich strukturach spełniających aksjomaty, to można go dowieść, i odwrotnie, posiadanie dowodu gwarantuje prawdziwość. Do tej struktury dołączamy następne prawa określające jak pojęcia które opisujemy mają sie do siebie. I właśnie określenie owych własności symboli, obiektów czy stałych to aksjomaty. Te DODATKOWE aksjomaty dotyczą relacji pozalogicznych. Jeszcze raz – dodajemy aksjomaty dotyczące obiektów zdefiniowanych poza logiką ( liczb, zbiorów, obiektów grupy, obiektów geometrycznych). I wówczas nie sposób powiedzieć jakie własności będzie miał cały system. Czy będzie niesprzeczny? Czy każde twierdzenie które ma dowód będzie prawdziwe we wszystkich strukturach spełniających aksjomaty? Czy każde prawdziwe twierdzenie będzie miało dowód? Na te pytania NIE MA ODPOWIEDZI dlatego że struktura która rozważamy jest zbyt ogólna. W ogólności można w ten sposób dostać systemy formalne zupełne i niezupełne. Stąd trzeba wiedzieć więcej by na pytania odpowiedzieć. Odpowiedź zawarta jest w tw. Goedla o niezupełności.
Po pierwsze trzeba wiedzieć o jakich aksjomatach sie mówi. nie jest to obojętne – bowiem ta sama intuicyjnie rozumiana „teoria w ogóle” jak powiedzmy „liczby naturalne”, „teoria zbiorów”, „teoria wielomianów” itp. może mieć wiele nierównoważnych aksjomatyzacji, każda spełniająca pewien zbiór naszych oczekiwań czy wyobrażeń o własnościach jakie powinna spełniać owa „teoria w ogóle”. Okazuje się że np dodanie pewnych aksjomatów takich jak opisują ciało rzeczywiste ( https://en.wikipedia.org/wiki/Real_closed_fields ) daje w wyniku teorię zupełną. Geometria Euklidesa także jest teorią zupełną. Istnieją formalizację arytmetyki liczb naturalnych które mają tą własność ( https://en.wikipedia.org/wiki/Self-verifying_theories). Warto zwrócić uwagę na fakt, że znaczenie aksjomatyzacji Peano ( inne niż historyczne ) leży w tym że WYDAJE nam się iż opisuje ona nasze WYOBRAŻENIE o własnościach liczb naturalnych. No ale akurat tak jest że aksjomatyzacja Peano nie ma własności zupełności ( o czym mówi tw. Goedla). W tym kontekście ( nieco sarkastycznie i z przekąsem) kwestia że tak jest i że stanowi to dla nas zaskoczenie więcej mówi o naszych wyobrażeniach niż o samej arytmetyce. No ale nie powoduje to znaczących problemów, gdyż niesprzeczności i zupełności aksjomatyki Peano można dowieść i to na dwa sposoby ( indukcją pozaskończoną -> Gentzen, lub w ramach aksjomatyki teorii mnogości ZFC). Widać zatem że ISTNIEJĄ dowody poprawności czy prawdziwości aksjomatów, tyle że prawdziwość aksjomatów jednej teorii dowodzi sie wyrażając je w języku innej teorii. Dlaczego tak jest?
4. Pojęcie prawdy mówi o własności która nie jest precyzyjnie zdefiniowana. Na temat definicji prawdy toczą sie nadal aktywne dyskusje. Istnieje wiele możliwych formalizacji tego pojęcia, wszakże najszerzej przyjmowana jest znana koncepcja Tarskiego ( która wymaga relatywizacji prawdy do metajęzyka opisującego język formalny). Jest to niedoskonała koncepcja, ale przyjęta i działająca, o ile nie mnożymy bytów ponad potrzebę. Stwierdzenie prawdziwości danego twierdzenia w danej teorii, wymaga w jej ramach rozważenie wszystkich struktur spełniających aksjomaty tej teorii ( np. aksjomaty teorii grup spełnia każda grupa, która tym samym jest modelem teorii grup), i sprawdzenie czy twierdzenie które sprawdzamy, jest prawdziwe w każdej, z nich. Oczywiście to beznadziejne zadanie, ale nikt tak nie postępuje! Konstrukcja ta służy wyłącznie definicji prawdy – prawdziwe twierdzenie to takie które zachodzi we wszystkich modelach teorii. Tymczasem matematycy w praktyce zawodowej posługują sie dowodem. A dowód – to jak pisaliśmy wyżej to manipulacja napisami. Skąd wiadomo że taka manipulacja daje nam uzasadnienia dla prawdziwości twierdzeń? Ano z twierdzenia o pełności logiki, które stwierdza że jeśli reguły inferencji ( a w praktyce tylko modus poens) zachowują własność prawdziwości ( czyli od zdań prawdziwych prowadzą do zdań prawdziwych) to mamy równoważność obu pojęć – to co daje sie dowieść jest prawdziwe a to co prawdziwe daje sie dowieść. I w tym miejscu następuje wielkie zdziwienie, a jego powodem bynajmniej nie jest tw. Geodla ale twierdzenie Trachtenbrota które stwierdza, że aby logika była zupełna, nie może być strukturą finitystyczną. Ludzkim językiem idzie to tak: jeśli rozważymy logikę klasyczną realizowaną wyłącznie na strukturach skończonych to taki system nie jest zupełny. Czyli rozumowanie logiczne wymaga nieskończoności. Przy takich założeniach, logika jest zupełna i JEŚLI prawdziwe sa zdania które do niej dodaliśmy jako aksjomaty ( Geometrii Euklidesa, Arytmetyki Peano, Ciałą Rzeczywistego, Teorii Zbiorów itp.) to to co dowiedzione jest prawdziwe we wszystkich modelach. Niestety – jak wiadomo z tw. Geodla – to co prawdziwe we wszystkich modelach – nie zawsze jest dowodowe a łyżką cudnej przyprawy która czyni smak matematyki ciekawy jest arytmetyka Pano, która „psuje teorie” jeśli sa one na tyle „wygadane” by ja wyrazić w swoim języku. N ale jak ktoś chce mieć całkiem banalną matematykę bez owej przyprawy – proszę bardzo – wystarczy używać słabszych aksjomatyk dla liczb naturalnych – i będzie miał wszystko dowodliwe. Tyle że to trochę tak jak jeść potrawy bez soli. Co jest najważniejszym wnioskiem z powyższego? Ano że tak jak dowód prawdziwości twierdzenia wykonuje sie w oparciu o aksjomaty, tak prawdziwość aksjomatów DOWODZI sie w oparciu o teorie które pozwalają owe aksjomaty wyrazić w swoim języku. Czyli prawdziwość – twierdzeń czy aksjomatów jest RELATYWNA. Relatywna do uniwersum w którym dane pojęcia rozważamy.
A „Prawda W Ogóle”? Chętnie o niej pogadam – niechże tylko ktoś wyjaśni o czym mówi…
(**) Helenra Rasiowa wydała kilka książek w których dokonała daleko idącej formalizacji wykładu podstaw matematyki. Oczywiście takie podejście do matematyki w ogóle ( powiedzmy do tw. Fermata, do tw. Poincare dowiedzionego przez Perelmana, do zagadnienia rozwiązań równania Naviera-Stokesa, do kwestii Hipotezy Riemanna itp.) jest szalenie trudne, właściwie niemożliwe, najpewniej bezsensowne. W przeszłości takimi metodami badano podstawy matematyki, a celem tych prac było raczej wyeliminowanie kłopotów niż koncepcja rekonstrukcji matematyki. Niemniej warto zwrócić uwagę, że podejście formalne zdało sie złapać drugi oddech, a przynajmniej nabrać ciała, przez wykorzystanie komputerowych systemów dowodów. Zwrócę tu uwagę na dwa „produkty”. Jednym z nich jest system MIZAR autorstwa Andrzeja Trybulca. jest to zdecydowanie największy wynalazek Polskiej matematyki 2-giej połowy XX wieku, chyba całkowicie zapoznany w kraju, a szkoda, skoro daje niezwykłe możliwości rozwoju. System ten posiada obecnie najbardziej rozbudowaną bibliotekę twierdzeń matematycznych na świecie, w której całkowicie formalnie sprawdzono logiczną poprawność 49000 twierdzeń zapisując je w aksjomatyzacji Teorii Mnogości. http://mizar.org/project/ Składnia systemu odpowiada niemal że językowi naturalnemu. Proszę sobie wyobrazić jakie meta-analizy są możliwe w oparciu o taką bazę danych! NIKT TEGO NIE ROBI.
Innym ciekawym przykładem jest Univalent Foundations które idzie w kierunku odwrotnym. Za pomocą COQ zapisano w języku formalnym pewną aksjomatyzację podstaw matematyki, a na tej podstawie stworzono (napisano?) książkę opisującą zawartość tego systemu. Być może tka będzie wyglądała przyszłość jakiegoś fragmentu matematyki: http://homotopytypetheory.org/
Ilekroć pojawia się na tym blogu wpis o matematyce, po przejściu do komentarzy zaczynam mieć deja vu. Te same osoby podają te same argumenty na temat klęski matematyki, inne osoby tak samo jak poprzednio argumentują, by tej matematyki bronić. Zawsze pojawia się też sugestia, że oprogramowanie na tym blogu zostało napisane przez matematyków (na jakiej podstawie, nie wiem, być może, jeśli tak chętnie poznam ich nazwiska).
Co do klęski matematyki w naukach fizycznych, poprosiłbym szanownych krytyków o zaproponowanie lepszych rozwiązań, zapewniam, że jeśli je podadzą, to fizycy w większości bez żadnych sentymentów porzucą metodę matematyczną, są to ludzie praktyczni, matematykę traktują raczej użytkowo, głównie dlatego, że jak na razie działa lepiej niż inne rzeczy, których próbowali. Dlatego właśnie starają się weryfikować doświadczalnie przewidywania oparte na matematyce, z dość dużymi ostatnio sukcesami, jak w przypadku odkrycia bozonu Higgsa, czy podobno ostatnio fal grawitacyjnych. Jeśli to są te spektakularne klęski świadczące o problemach nauk fizycznych, spowodowanych matematyką, to oby takich więcej.
Jeśli zaś chodzi o teorię strun, problem opisał kiedyś Dyson (skądinąd fizyk matematyczny) i to o ile pamiętam w wywiadzie dla Polityki. Zbyt wiele wydziałów okryło, że tanim kosztem, bez nakładów na laboratoria można stworzyć grupę naukową i postawiło właśnie na modną wówczas teorię strun. Ruszyła lawina i rzeczywiście odciągnęło to wielu młodych ludzi od badania bardziej weryfikowalnych teorii, ze szkodą dla fizyki (i moim zdaniem tylko umiarkowaną korzyścią dla matematyki, ale być może sam zajmuję się zbyt przyziemną matematyką, by docenić należycie teorię strun, zwłaszcza, że nie byłbym w stanie nic z niej zrozumieć). Przyczyny więc (jeśli wierzyć Dysonowi, ale ja wierzę, bo na pewno zna te realia lepiej niż ja) miały charakter środowiskowy, a nie merytoryczny.
Ogólnie śmieszy mnie cały ten spór na temat matematyki, zwłaszcza, gdy ktoś krytykuje, a nie proponuje nic w zamian, a ktoś inny uważa matematykę za panaceum, albo przecenia samych matematyków. W tym ostatnim kontekście, zawsze drażniła mnie arogancja a la Steinhaus w stylu „Matematyk zrobi to lepiej”, sam jestem matematykiem, ale obawiam się, że przeciętny matematyk większość rzeczy zrobi raczej gorzej, albo wcale, chyba że będzie kontrolowany przez specjalistę w danej dziedzinie, wtedy współpraca może przynieść naprawdę dobre efekty.
Natomiast znamienne jest, że wpis na temat twierdzenia Goedla i geometrii nieeuklidesowych jak zwykle prowadzi do dyskusji nie na temat, która sama w sobie mogłaby pewnie być interesująca, gdyby nie to, że była już tu wałkowana po stokroć w takim samym wydaniu i z mniej więcej takim samym efektem. Aż mi samemu głupio, że się tu odzywam.
@xxx – właściwie to podobnie jak argumentum ad hitlerium należałoby wprowadzić argumentum and goedlum i uważać ze ten kto w dyskusji o matematyce użył tw. Goedla sromotnie przegrał z powodu braku argumentów…
Sądzić se można, co się chce, także o sromocie. Inna sprawa, jak się nie ma poważnych argumentów i próbuje bezpodstawnie zdezawuować wypowiedzi przeciwnika.
Nie znam się na tych wszystkich strunach i membranach, ale ponad 20 lat temu poznałem tę osobę i powiem Wam, że to ogromna przyjemność mieć z nią do czynienia.
Po latach obserwacji i kontaktów z ludźmi z różnych dziedzin nauki doszedłem do wniosku, że najbardziej wszechstronne zainteresowania poza własną profesją mają fizycy. Muzyka, sztuka, kultura w najszerszym pojęciu, ale także rzadkie dyscypliny sportowe… Da się z nimi pogadać i pomuzykować, powspinać i pochodzić po jaskiniach, ale też naprawić gontowy dach i ugotować dobrą kolację 😉
@xxx: „Ogólnie śmieszy mnie cały ten spór na temat matematyki, zwłaszcza, gdy ktoś krytykuje, a nie proponuje nic w zamian”
Na ogol matematyke krytykuja ci ktorzy nie maja o niej zielonego pojecia. Ot, taki sposob „odkompleksowiania sie”.
Zas jak komus nei podoba sie matematyka taka jaka jest, to sa rozne warianty: „non-standard calculus” czy matematyka z ktorej usunieto pojecie neiskonczonego zbioru. Proponuje pogoglwoac.
Tyle, ze jak mnie sie zdaje, te inne matematyki wcale nie sa lesze od tej niedobrej.
Tak na marginesie, jest piekna a elementarna ksiazeczka z wprowadzeniem od geometrii neiuklidesowej: Stefan Kulczycki, Geometria Nieeuklidesowa, PWN 1960. Calkiem neidawno zostala wydana w wersji angielskiej przez wydawnictwo Dover (2008 rok). Polecam gdyby ktos sie interesowal. Dostepan dla ucznai skoly sredniej z zamilowaniem do matematyki
@xxx
1. Niestety, ale fizycy wlozyli za duzo czasu, a czesto tez i pieniedzy w swa obecna edukacje matematyczna, aby porzucic ta obecna matematyke, pomimo iz ona wyraznie sie nie sprawdza w zderzeniu z rzeczywistoscia.
2. Tw. Boska czasteczka (bozon Higgsa) czy tez fale graitacyjene wcale nie zostaly wykryte, jako iz sa to byty tak ulotne, praktycznie niematerialne (sczegolnie te fale grawitacyjne) ze sie ich po prostu wykryc nie da. Wykryto tylko zjawiska, ktore zostaly (blednie zreszta) zinterpretowane jako owe bozony czy tez fale. Ale fizyka potrzebuje na gwalt sukcesow (ogromne wydatki na nia), a wiec sie je sfabrykowalo. Jak to juz pisalem, Hollywood potrafi dzis wyprodukowac tak doskonale imitacje np. stanu niewazkosci, ze ogladajac je (szczegolnie w 3D) nie zdajemy sobie czesto sprawy, ze to jest tylko symulacja komputerowa.
3. Ja proponuje zmiany, a mianowicie poszukiwanie innej matematyki, tym razem bardziej zgodnej z nasza rzeczywistoscia. Jak to przypomnial nam AL, matematyk jest rodzajem krawca, ale nie musi on przeciez byc szalony – moze rownie dobrze szyc ubrania na istoty realnie istniejace, a nie tylko na wyimaginowane, jak to sie dzis dzieje.
@A.L.
1. Akurat ja o matematyce wiem sporo jako absolwent ekonometrii na calkiem dobrej zachodniej uczelni (najlepsza w rankingach swiatowych na swoim kontynencie) . Aby wyprzedzic kontrargumenty: calki, rozniczki, geometrie analityczna oraz wykreslna mialem juz w szkole srednej, a rachunek macierzowy na pierwszym roku studiow (w Polsce).
2. Ekonomisci nie sa winni tego, ze matematycy dali im do reki zle narzedzie. Podobnie jest przeciez z fizykami. Raz jeszcze powtarzam, nawiazujac do Lema, ze matematyk jest rodzajem krawca, ale nie musi on przeciez byc szalony, jako iz moze ron ownie dobrze szyc ubrania (jak np. zona jednego z naszych skoczkow narciarskich) na istoty realnie istniejace, a nie tylko na wyimaginowane, jak to sie dzis dzieje w matematyce.
3. Naprawa matematyki musi byc zas gruntowna ? tu nie wystarczy usuniecie jednego aksjomatu, tu trzeba usunac wszystkie aksjomaty, a wiec zaczac niejako od fundamentow. Nie mozna bowiem opierac jezyka nauki (czyli matematyki) na z definicji nieudowadnialnych aksjomatach. Budowa nowej matematyki jest bowiem niezbedna ? inaczej nigdy nie uda sie fizyce stworzyc OTW(szystkiego), czyli polaczyc w jedna spojna calosc mechaniki kwantowej z OTW(zglednosci).
4. Zgoda – celem matematyki NIE jest opisywanie czegokolwiek, ale takie matematyki, ktore niczego nie opisuja, nie maja po prostu sensu. My tu zas dyskutujemy o zastosowaniach matematyki, a do tych, nadaje sie tylko taka matematyka, ktora opisuje nasz relany swiat. Inne matematyki mnie zas nie intresuja, choc oczywiscie moga byc one ciekawe dla matematyka. Ale te inne matematyki, opisujace nierealne swiaty, powinny byc traktowane jako hobby matematykow, a wiec nie powinny byc one finansowane przez podatnikow.
5. Oprogramowanie tego blogu wyraznie jest ?dzielem? matematykow (programistow z matematycznym wyksztalceniem), gdyz tylko matematyk moze wymyslc cos tak pokracznego jak to oprogramowanie. 😉
@mpn
1. Nie wiem, na czym ma byc oparta ta nowa matematyka (to jest zadanie dla matematykow), ale wiem, ze nie moze byc ona oparta na nieudowadnialnych aksjomatach.
@kakaz
1. A co z argumentem ad Cantorum – myslenie o nieskonczonosciach prowadzi wybitne umysly do obledu, jako iz nieksonczonosc jest pojeciuem wewnetrznie sprzecznym?
Pozdrawiam wszystkich uczestnikow tej dyskusji!
@kagan: „Aby wyprzedzic kontrargumenty: calki, rozniczki, geometrie analityczna oraz wykreslna mialem juz w szkole srednej, a rachunek macierzowy na pierwszym roku studiow (w Polsce).”
Z szacunkiem, ale to co Pan wymienil to nei jest matematyka. To sa RACHUNKI. W szczegolnosci w wydaniu dla ekonometrystow czy inzynierow. Proponuje wiec nei uzywac ich w kontekscie dyskusji o MATEMATYCE
@A.L.
1.Bardzo prosze bez ad personam: calki, rozniczki, geometrie analityczna oraz wykreslna a takze rachunek macierzowy i rachunek prawdopodobienstwa wraz ze statystyka matematyczna (ktore tez mialem w szkole sredniej oraz na studiach) naleza do tzw. matematyki wyzszej.
2. A poza tym, to nie ekonomisci sa winni temu, ze obecnie znana matematyka sie nie sprawdza w ekonomii, ale matematycy, ktorzy dostarczaja ekonomistom wadliwe narzedzia matematyczne. Gdyby owe narzedzia byly dobre, to dawno temu znalazlo by sie sporo matematykow, ktorzy by je z sukcesem zastosowali w ekonomii. Zas brak takowych matematykow swiadczy tylko o tym, ze obecnie znana matematyka opisuje jakichs fikcyjny swiat, niewiele majacy wspolnego ze swiatem, w ktorym zyjemy.Finasowanie takiej matematyki z pieniedzy podatnikow nie ma wiec nic wspolnego z demokracja oraz uczciwoscia.
Szalom!
@kagan „A co z argumentem ad Cantorum ? myslenie o nieskonczonosciach prowadzi wybitne umysly do obledu, jako iz nieksonczonosc jest pojeciuem wewnetrznie sprzecznym?” – dlaczego? Jakoś Pan to uzasadni? Zdaje sie akurat sprzeczności tu nie ma. Natomiast są kłopoty pojęciowe, n ale co w tym dziwnego skoro to rzecz tak odległa od codzienności? Znacznie bardziej kłopotliwe dla umysłu sa zagadnienia Mechaniki Kwantowej, gdzie mamy do czynienia z niekomutatywną teorią prawdopodobieństwa, a jakoś wariatów nie ma za wielu wśród fizyków ( no!) 😉 Poza tym można byc iść dalej. Skoro Cantor nabrał kłopotów umysłowych z powodu nieskończoności, cóż nas powstrzymuje przed dalszymi wnioskami?
Osobiście sądzę że algebra liniowa jest moczopędna, a zajmowanie sie nią zawodowo powoduje w dłuższej perspektywie choroby nerek. Pozostaje przeprowadzić badania przesiewowe – jest to teza naukowa bo dopuszcza falsyfikację!
Geometria różniczkowa i teoria liczb – zdecydowanie choroby płuc, gruźlica ( Riemann).
Syn Hilberta był niepełnosprawny umysłowo, co sugeruje że wymyślanie problemów i zajmowanie stanowiska formalizmu daje wpływy jeśli chodzi o genetykę.
Itp. itd.
@kagan
„Wykryto tylko zjawiska, ktore zostaly (blednie zreszta) zinterpretowane jako owe bozony czy tez fale.”
Nie poproszę o żaden argument na to, że ta interpretacja jest błędna, bo wiem, że go nie podasz. Chyba, że wykształcenie w dziedzinie fizyki masz równie dobre jak z matematyki i nas zaraz zagniesz.
W prąd elektryczny też pewnie nie wierzysz, bo go nie widziano, a tylko zinterpretowano…
„Ja proponuje zmiany, a mianowicie poszukiwanie innej matematyki, tym razem bardziej zgodnej z nasza rzeczywistoscia.”
To powodzenia w poszukiwaniach, jak już ją znajdziesz, odezwij się jeszcze, bo na razie to nie jest żadna propozycja, tylko takie ględzenie, że trzeba zrobić coś by było lepiej. Ja więc na razie zawieszam swój udział w dyskusji i niecierpliwie czekam na konkretne osiągnięcia Twojej nowej matematyki. Proszę mi nie odpowiadać, dopóki ich nie będzie (to by tylko niepotrzebnie oderwało Cię od pracy, ludzkości na to nie stać, bo problem z fizyką i matematyką jest zbyt palący). Mam nadzieję, że porozmawiamy już wkrótce (nie mogę się doczekać).
@kaganL :Bardzo prosze bez ad personam: calki, rozniczki, geometrie analityczna oraz wykreslna a takze rachunek macierzowy i rachunek prawdopodobienstwa wraz ze statystyka matematyczna (ktore tez mialem w szkole sredniej oraz na studiach) naleza do tzw. matematyki wyzszej.”
Nie przypominam sobie abym uzywal argumentwo ad-persona. W koncu, nei dyskutowalem jakosci Panskiej uczelni. Owa matematyka ktora Pan opisal, to matematyka „wyzsza” dlatego ze sie aj wykalda na „wyzszej” uczelni. Jako inzynier wiem jak sie naucza matematyki inzynierow, I jakiej. Jako krecacy sie wokol szkol ekomomicznych, wiem jak sie tam naucza matematyki I jakiej. A jako osobnik ktory zaliczyl 5 lat matematyki na Uniwersytecie Warszawskim, wiem czym sie owa matematyka rozni od inzynierskiej.
„A poza tym, to nie ekonomisci sa winni temu, ze obecnie znana matematyka sie nie sprawdza w ekonomii, ale matematycy, ktorzy dostarczaja ekonomistom wadliwe narzedzia matematyczne”
Panskei narzekanai przypominaja mi narzekania faceta ktoremu dostarczono nowoczesna, elektronicznie sterowana wiertarke elektryczna, a on stwierdza ze jako mlotek to ona sie kiepsko sprawdza.
Nei szujakac daleko, modele regresyjne czy modele szeregow czasowych na przykald ARIMA konstruowane byly ptzy zalozeniu ze czynniki losowe maja okreslone wlasnosci statystyczne, konkretnie rozkald prawdopodobienstwa I autokorelacje (w modelach regresyjnych wymagany jest brak autokorelacji). Tylko przy takich zalozenaich mozliwe jest stosowanie testow statystycznych I wyciaganei wnioskow na podstawie tych testow. Chcialbym zobaczyc prace ekonometryczna w ktorej bylby testy czy owe zalozenie sa spelnione. Nikt sobie tym glowy nei zawraca. Wrzuca sie dane do pudelka, kreci korbka – I jest
Jest caly szereg publikacji powaznych facetow twierdzacych ze ostatni kryzys ekonomiczny spowodowany byl pzrez ekonomistow, uzywajacych „na chama” I bez zrozumienia modeli ktore w okreslonych warunkach sie nei nadawaly. Byly to modele sluzace do zupelnei innych celow niz te do ktorych byly uzyte. Linki podawale przyejdnej z poprzednich dyskusji, wiec nei bede sie powtarzal.
W kwestii podniesionej pzrez xxx, pytanei do Gospodarza, w zwiazku z jego „manifesto” na temat porzadku na blogu: czy nie mozna uznac ze systematyczne wyjezdzanie z niekonstruktywna I bezpzredmiotowa krytyka matematyki jest „nei na temat”?
Chciałbym podziękować wszystkim blogowym terapeutom i pielęgniarzom za zajęcie się ciężkim przypadkiem i tym samym za umożliwienie mi zrobienia zakupów, posprzątania w domu i takiego ogólnego ogarnięcia się. Bez waszej pomocu byłoby to niemożliwe.
@kakaz
1. Pojecie nieskonczonosci jest wewnetrznie sprzeczne, jako iz dla kazdej racjonalnej liczby (racjonalnej w sensie ogolnym, czyli zgodnym z empiria, a nie w waskim sensie, jak to przyjeto obecnie w ortodoksyjnej matematyce), to N+1>N, ale nie dla nieskonczonosci ? ergo pojecie nieskonczonosci jest wewnetrznie sprzeczne, co doprowadzilo (m. in.) Cantora do obledu.
2. Reszty nie komentuje, bo bez sensu.
@xxx
1. Podobno fizycy wykryli jakies zajwiska, ktore uznali oni za dowod na istnienie tzw. boskiej czasteczki (pewnego rodzaju bozonu) oraz fal grawitacyjnych, ale nie wykryli oni przeciez ani tej czasteczki, ani tez tych fal. Po prostu tyle wydaje sie ostanio na fizyke, ze fizycy sa pod wielka presja znalezienia jakich wynikow, ktore by usprawiedliwialy owe ogromne przeciez wydatki. A poniewaz brak jest realnych wynikow (np. wciaz nie udaja sie eksprymenty z praktycznym wykorzystaniem zjawiska synetzy jadrowej jako zrodla energii, to szuka sie substytutow, np. w postaci wykrycia owych tzw. boskich czasteczek). A tymczasem, to cala wspolczesna fizyka okazuje sie niespojna, jako iz mechanika kwantowa jest fundamentalnie wrecz niezgodna z ogolna teoria wzglednosci, z czego wynika, ze grawitacja jest dalej zle zroumiana, a wiec najprawdopodobniej to ogolna teoria wzglednosci jest jednak bledna, jako iz mechanika kwantowa zdolala ujednolicic wszytskie pozostale sily czy tez pola, ale poza grawitacja, a z drugiej strony to najprawdopodobniej teoria stojaca za synteza jadrowa jest bledna, jako iz w laboratorauch nie udalo sie przeciez wytworzyc sztucznego slonca w tym sensie, ze reaktory termojadrowe maja dzis, w odroznieniu od gwiazd, ujemny bilans energetyczny, pomimo iz istnieja owe reaktory juz od ponad pol wieku (koncepcję tokamaka stworzono przeciez na pocztaku lat 1950tych).
2. Prad elektryczny jest zas czyms zupelnie innym niz boskie czasteczki czy fale grawitacyjne, jako iz mozna go wyczuc naszymi zmyslami (choc nie polecam eksperymentow z pradem z gniazdka domowego).
3. Niestety, matematycy wraz fizykami zbyt duzo wlozyli w obecna, ortoksyjna matematyke, aby odwazyc sie na jej odzrzucenie. Ale zostana oni do tego zmuszeni, kiedy okaze sie wszem i wobec, ze fizyka stoi do wielu lat w miejscu, a te ogromne pieniadze wydawane na nia sa dzis juz tylko pieniedzmi zmarnowanymi. Niestety,ale jedynym obiektywnym testem dla teorii naukowej jest jej praktyczne zastosowanie, a wiec to niemozliwosc parktycznego zastosowania wynikow badan przeprowadzanych dzis przez fizykow spowoduje, ze te badania przestana byc finasowane przez podatnikow, co dopiero zmusi fizykow, a posrednio tez i matematykow, do pracy na nowa matematyka, tym razem opisujaca nasz realny wszechswiat.
@A.L.
1. Tylko matenmatyka, o ktorej piszesz z pogarda jako inzynierskiej, ma sens, jako iz ona sie sprawdza w praktyce. Reszta matematyki to jest wynik dzialan owych szalonych krawcow, ale po co mam szaleni krawcy? Oni wrecz sa niebezpieczni dla otoczenia ze swymi ostrymi nozycami! 😉
2. Jesli porownujemy matematyke do wiertarki, to ja bym ja porownal do takej wiertarki, ktora sie wciaz zacina oraz do ktorej nie pasuja dostepne na rynku wiertla. Po prostu matematycy nie sa dzis w stanie dostarczyc ekonomii uzytecznych matematycznych narzedzi,a wine zwalaja ci matematycy nie na siebie, czyli na dostawcow bezuzytecznych, wadliwych narzedzi, a na bogu duch winnych uzytkownikow tych wadliwych narzedzi matematycznych, czyli na ekonomistow.
3. Poza tym, to czynniki losowe w praktyce czesto nie maja zadnych okreslonych wlasnosci statystycznych, jako iz sa one losowe. A wtedy to ortodoksyjna teoria prawdopodobienstwa, oparta na ortodokosyjnej matematyce zawodzi z definicji.
4. Zgoda, ekonometrycy z reguly bezmyslnie uzywaj komputerow, ale to jest wynik tego, ze nie znaja oni dobrze teorii ekonomii, a wiec wydaje im sie, ze realna gospodarka da sie opisac przy pomocy znanych im narzedzi formalnych. Problem lezy tu nawet bardziej w niedostatkach obowiazujacej obecnie na uniwersytetach ortodoksyjnej teorii ekonomii niz w ograniczeniach narzedzi matematycznych znanych oraz dostepnych dzis ekonomistom.
5. Widze, ze z braku sily argumentow, siegamy do argumentu sily. 🙁
6. I dlaczego matematyka miala by byc ponad krytyka? Przeciez prawdziwa cnota krytyk sie nie boi!
@zza kałuży
1. Widze, ze z braku argumentow ad rem,siegamy po argumenty ad personam. 🙁
@kagan: „Tylko matenmatyka, o ktorej piszesz z pogarda jako inzynierskiej, ma sens, jako iz ona sie sprawdza w praktyce. Reszta matematyki to jest wynik dzialan owych szalonych krawcow, ale po co mam szaleni krawcy?”
O ile pamietam, proetstowal Pan rozniez pzreciwko pochodnym, bo te opieraja sie na pzrejsciach granicznych I wielkosciach neiskonczenie malych.
A ci „inni krawcy” tez sie przydaja. Nei wiem czy Pan wie, ale praktyka „control engineering” opiera sie dzis w znacznym stopniu na teorii zwanej H-infinity. To teoria bazujaca na specjalnych przestrzeniach Hardy-Lebesque, ktore same w sobie sa pzrestrzeniami Banacha. Ta teoria, do ktorej matematyczne wyksztalcenei inzynierskie nei wystarcza, okazala sie calkiem praktyczna. Bez tej teorii samoloty by nei lataly, rakiety by nei lately, I pare rzeczy by nei latalo. Pdobnie w „control engineering” przydaja sie pewne dosyc specjalne pzrestrzenie Hilberta, zwane przestrzeniami Sobolewa. Przydaly sie miedzy innymi do tego zeby International Space Station leciala stabilnie, a nie kiwala sie na boki. Dlatego tez wlasnie, jako automatyk, studiowalem matematyke. Dla inzyniera automatyka wykraczajacego poza walcownie stali czy petrochemie wyksztalcenie inzynierskie okazalo sie niewystarczajace.
Przydaje sie rozniez na przyklad dosyc abstrakcyjna teoria krzywych eliptycznych. Do konstrucji algorytmow szyfrujacych na przykald. Zarownio pzrestrzenie Hardy-Lebesque jak I krzywe eliptyczne jeszcze calkiem niedawno nei mialy zadnych zastosowan. Wiec proponuje ostroznie z ta nieprzydatnoscia matematyki.
„Poza tym, to czynniki losowe w praktyce czesto nie maja zadnych okreslonych wlasnosci statystycznych, jako iz sa one losowe”
Pzrepraszam, ale to zdanie jest wewnetrznei sprzeczne. Nonsensowne. Nei mowiac o tym ze nei ma sensu. O statystyce, procesach stochastycznych, rachunku prawdopodobienstwa Pan zapewne nei slyszal
„a na bogu duch winnych uzytkownikow tych wadliwych narzedzi matematycznych, czyli na ekonomisto”
No wlasnie. Wiertarka jest wadliwa bo kiepsko nai sie wbija gwozdzie. Wiec producent wieertarki winien.
@A.L.
1. Protestowałem przeciwko nadużywaniu pochodnych, jako iż są one zbyt mocno powiązane z nieskończonością – w wielkim skrócie różniczka nazywa się po polsku różniczką, jako iż jest to, w wielkim skrócie nieskończenie mała różnica, całka nazywa się całką, jako iż jest to (także w ogromnym skrócie) niejako całość powstała z nieskończonej ilości nieskończenie małych części. Oczywiście, można (i powinno się) używać różniczek oraz całek w mechanice klasycznej, czyli rozpatrując relatywnie niskie wartości takich parametrów jak n.p. szybkość czy masa, ale jednym wielkim nieporozumieniem jest używanie różniczek czy też całek w mechanice kwantowej czy też teorii względności (ogólnej oraz szczególnej), czyli tam, gdzie mamy do czynienia z wielkościami albo bardzo małymi albo też bardzo dużymi. Wychodzą nam wtedy takie pokraki jak n.p. to, że teorie związane z kwantową teorią pola (mechaniką kwantową) dają zwykle skończone i poprawne wartości wielkości mierzalnych, takich jak prawdopodobieństwa rozpraszania cząstek czy czasy życia układów złożonych jak n.p. nukleony tylko wtedy, jeśli założy się, NIEZGODNIE Z FIZYCZNA RZECZYWISTOŚCIĄ, że wartości parametrów modelu mają nieskończone wartości. Innymi słowy n.p. wartość parametru reprezentującego ładunek na przykład elektronu musi mieć wartość nieskończoną, aby poprawnie opisać cząstki jądrowe i ich reakcje. Oczywiście, taka teoria pola nie jest z definicji naukowa (oparta jest ona bowiem na błędnych, nierealistycznych założeniach), a więc powinna być ona z miejsca odrzucona, a tymczasem fizycy sztucznie utrzymują takiego trupa przy życiu poprzez nienaukową z definicji procedurę renormalizacji.
2. Nie mam nic przeciwko szalonym krawcom, jeśli pracują oni na swój własny rachunek oraz nie zmuszają innych do uczenia się ich teorii.
3. Samoloty latają od początku XX wieku, pomimo iż bracia Wright oraz inni pionierzy awiacji na 100% nie mieli pojęcia o teorii zwanej H-infinity.
4. International Space Station jest nam potrzebna jak wrzód na pewnej tylnej części ciała.
5. Algorytmy szyfrowania najbardziej przydają się gangsterom oraz skorumpowanym politykom.
6. Nigdzie też nie napisałem, że matematyka jako taka jest nieprzydatna. Ja tylko opisuje nieprzydatność oraz ograniczenia obecnie znanej matematyki, czyli tej nauczanej na wydziałach matematyki praktycznie wszystkich uniwersytetów.
7. Proces losowy jest z definicji nieprzewidywalny. A jeśli jakiś proces jest przewidywalny, to nie jest on losowy. Proponuję weryfikację tego, co tu napisałem n.p. w kasynie.
8. Mowa jest o dostawcy wadliwych wiertarek dla kogoś, kto chce nimi wiercić otwory, a nie dla kogoś, kto nie ma pojęcia o tym, do czego służy wiertarka. Za przeproszeniem, ale ekonomista, nawet ortodoksyjny, czyli neoklasyczno-monetarystyczny nie jest jednak małpą, która wali zegarkiem w ścianę czy też tym przysłowiowym polskim chłopem, wbijającym gwoździe przy pomocy zegarka.
Szalom.
Udowodniłem FLT. Twierdzenie oparłem na podzielności funkcji pierwotnej przez jej pochodną. Może kogoś to zainteresuje.
https://www.dropbox.com/s/cvpvelt4ea7qsei/Beal%20Conjecture%20and%20FLT_1.pdf
@kagan: „Proces losowy jest z definicji nieprzewidywalny. A jeśli jakiś proces jest przewidywalny, to nie jest on losowy. Proponuję weryfikację tego, co tu napisałem n.p. w kasynie”
A ja proponuje werfiakcje w jakims podreczniku. Procesy losowe doskonale sie daja prognozowac. Przynajmniej niektore.
Proponuje aby Pan troche sie przyuczyl matematyki zanim zaczie ja krytykowac.
@A.L.
1. Prawdziwy proces losowy to jest, taki, którego wyniki są nieprzewidywalne. A jeśli wyniki jakiegoś procesu dają się przewidywać, to znaczy, że rządzi nim jakiś mechanizm NIElosowy, a więc nie jest to z definicji proces losowy. A za bałagan w terminologii matematycznej, to już nie ja jestem odpowiedzialny. 2. I jeszcze raz powtarzam, że numery padające w prawdziwej grze losowej są całkowicie nieprzewidywalne. Niech tu przykładem będzie np. ruletka, ale taka nieoszukana. Zgoda, paść w niej mogą tylko te numery, które są na stole, czyli od 0 do 37 albo 38 (dokł. 00 – w zależności od odmiany tej gry). Ale w ruletce tak samo prawdopodobne jest, przynajmniej w teorii, ze będą padać po kolei same zera, jak każda inna sekwencja liczb od 0 do 37 (38/00). A z kolei wiemy z praktyki, ze pomimo iż w ruletkę grają codziennie (i conocnie) tysiące ludzi w setkach kasyn, to nie ma (przynajmniej dotychczas) takiej ruletki, gdzie ciągle padały by tylko i wyłącznie zera. Jedyne logiczne wyjaśnienie jest więc takie, że gra w ruletkę nie jest grą losową, a wiec jej wynikami rządzi jakichś mechanizm, o którym jednak nikt na razie nie ma pojęcia, jako iż gdyby ktoś poznał ten mechanizm, to kasyna by zwyczajnie, po pewnym czasie, zbankrutowały. A ze one na razie nie zbankrutowały, to znaczy, ze nikt na razie nie rozumie procesu sterującego wynikami gry w ruletkę.
3. Co więcej: dotychczas twierdzono, że chociaż ruch kulki jest ściśle zdeterminowany prawami mechaniki klasycznej, to koło ruletki jest jednak układem chaotycznym, a więc przewidzenie, na którym polu zatrzyma się kulka, jest niemal niemożliwe. Ale obecnie w kasynach pojawiła się ostatnio ruletka elektroniczna, gdzie wyniki są losowane przez komputer. W takim wypadku mamy do czynienia z jakimś algorytmem generującym liczby losowe, ale dobrze wiemy, że to są tylko liczby pseudolosowe, a więc, przynamniej w teorii, da się przewidzieć wyniki takiej elektronicznej ruletki. Proponuję więc matematykom rozpracowanie takiej elektronicznej ruletki, co dało by im o wiele lepsze publicity niż zmuszanie innych ludzi do uczenia się, w ogromnej większości przypadków, całkowicie dla nich bezużytecznej matematyki.
@RP
A co, jeśli dana funkcja jest nieciągła, a więc z definicji nie ma ona pochodnej?
@kagan: „A co, jeśli dana funkcja jest nieciągła, a więc z definicji nie ma ona pochodnej?”
Mialem juz nei odpowiadac, ale nie moge sie powstrzymac: funkcja nieciagla nei ma ppochodnej tylko w punkcie nieciaglosci. Chociaz – nic nei wiadomo. Sa funkcje ciagle wszedzie ktore nigdzie nei maja pochodnej. Z drugiej strony, dzieki teorii dystrybucji mozna uogolnic funkcje tak ze sa rozniczkowalne mimo nieciaglosci. Z grubsza rzecz biorac…
@A.L.
Nigdy nie watpilem w formalne mistrzostwo czolowych matematykow, czyli w ich bieglosc w przeksztalcaniu formulek matematycznych (w tym przeksztalcaniu nieskonczonosci w skonczonosci i na odwrot) oraz tworzenia, najczesciej zbednych, sztucznych, wirtulanych bytow. Tyle, ze w tej ostatniej sztuce to oni wciaz ustepuja filozofom, a sczegolnie zas teologom.
Szalom!
P.S.
Porownajmy np. wyobraznie filozoficzna takiego np. Leibniza z jego wyobraznia matematyczna. Nic nie ujmujac calkom czy rozniczkom, to czym one sa wobec Monad a przede wszystkim Harmonii Przedustawnej?
@kagan, @j.ty
Co do bledu patrz:
http://www.question-defense.com/2012/11/16/fast-secure-contact-form-error-could-not-read-captcha-token-file-try-again
@zFlorydy
Ta porada jest tyle sama warta co taka:
Problem: moj samochod pokazuje blednie komunikat: problem z silnikiem – jedz do najblizszej stacji obslugi.
Rozwiazanie: Zmien chip x1o1aB w komputerze na chip x101ab z wersja oprogramowania 3.2 rev.3 oraz przylutuj dodatkowo kondensator o pojemnosci pol pikofarada rownolegle do zielonego opornika w obowodze laczacym komputer z czujnikiem cisnienia oleju.
A na serio: ten problem powinien byc rowiazany przez tzw., geniuszy, ktorzy napisali to dziadowskie oprogramowanie. Jesli instaluje na swim koputerze np. Worda, to przeciez nie musze niczego zmieniac w root directory. Jak widac, matematycy potrafia wszystko sknocic…
Cytuje: The error above can be resolved by adding a folder named captcha-temp to the Fast Secure Contact Form?s root directory as shown in the below example shell output. Make sure to set the permissions to 777 using chmod to make it world readable/writable.
Aż z ciekawości sprawdziłem. Okazuje się, że główny twórca wordpressa ma wykształcenie wcale nie matematyczne, ale z nauk politycznych:
http://en.wikipedia.org/wiki/Matt_Mullenweg
Jakoś mnie to nie dziwi, doświadczenie wyniesione z dyskusji na tym blogu mówi mi, że specjaliści od nauk politycznych znają się na wszystkim, także na captcha related issues.
Chciałbym się nieśmiało przypomnieć moderatorom, mój poprzedni wpis miał link do wikipedii i trzy słowa po angielsku, przez co najwyraźniej utknął. Pozdrawiam.
@xxx
Linki podawaj bez tych trzech literek w i nastepujacych po nich trzech znakach niealfanumerycznych oraz pamietaj, że niektóre angielskie wyrazy są trefne dla amerykańskiego oprogramowania tego blogu.
Np. nietrefny link do tego wpisu to:
naukowy.blog.polityka.pl/2014/03/18/o-czym-milczy-matematyka/#comment-159894
Szalom!
Może skrócić linka oraz usunąć jego standardowy początek, np. tinyurl.com/l7xscm2