Złożona kwestia

23 listopada 2017
Blog szalonych naukowców

Niedawno wziąłem udział w spotkaniu, które miało poruszać m.in. kwestie prostoty i złożoności. Ostatecznie dyskusja poszła w inną stronę, ale samą kwestię mogę tu zarysować.

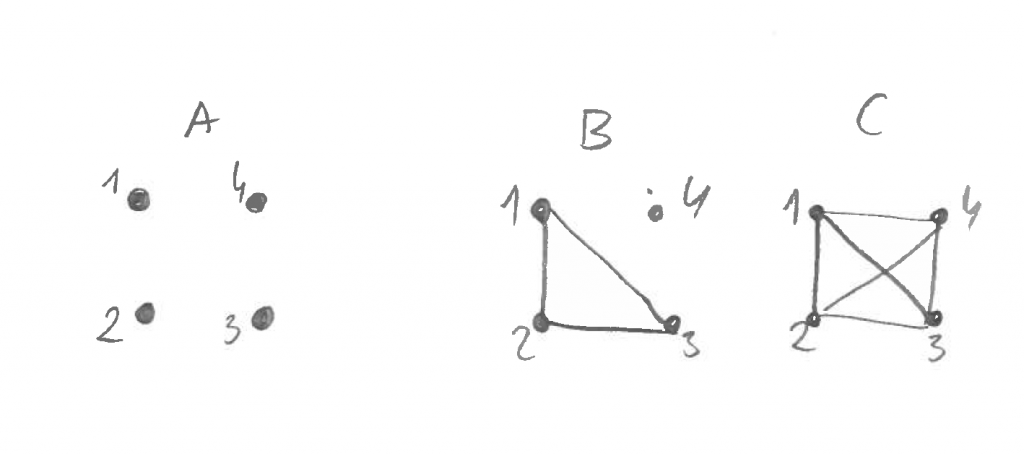
Przeanalizujmy sytuacje z obrazka. Sytuacja A wydaje się stosunkowo prosta – mamy cztery punkty. Nie są połączone. Właściwie nie ma o czym więcej mówić. To, że punkty są ponumerowane w kolejności odwrotnej od ruchu wskazówek zegara, nie ma większego znaczenia.

Sytuacja B jest na pewno bardziej złożona. Punkt 1 jest połączony z punktami 2 i 3, a punkt 2 dodatkowo z 3. Punkt 4 nie jest połączony z żadnym innym.

A sytuacja C? Wydaje się bardzo złożona. Punkt 1 jest połączony z punktami 2, 3 i 4. Punkt 2 ponadto jest połączony z punktami 3 i 4. Na dodatek punkt 3 jest połączony z punktem 4.

Ale zaraz, przecież sytuację C można opisać inaczej. Wszystkie cztery punkty są ze sobą połączone.

Poprzedni akapit jest przykładem kompresji opisu. Sytuację C można opisać zawile, połączenie po połączeniu, ale da się ją opisać też jednym zdaniem. W istocie sytuacja C jest praktycznie tak samo prosta jak sytuacja A. Są to sytuacje komplementarne, wzajemnie się dopełniające.

W teorii informacji złożoność i prostotę określa się właśnie przez długość opisu i ewentualną możliwość kompresji tego opisu. Zatem niektóre układy mogą się wydawać na pierwszy rzut oka bardzo złożone, a są w istocie całkiem proste. Tak jest z układem na obrazku C. Najbardziej złożona sytuacja jest na obrazku B, który wcale nie ma największej liczby połączeń. Warto o tym pamiętać, gdy dyskutuje się o złożoności i prostocie.

Tu przyznam, że mam pewien problem z liczbą π. Problem pojawił się właśnie w związku z przywołanym na wstępie spotkaniem. Otóż Karol Jałochowski, który jest fizykiem i twórcą tego bloga (choć teraz przeszedł do bardziej centralnej części POLITYKI), twierdzi, że π jest bardzo prosta. W końcu da się ją opisać banalnym równaniem – jest ilorazem obwodu koła (okręgu) do jego średnicy. Mnie jednak to nie do końca przekonuje. Owszem, sam wzór na obliczanie π jest prosty, ale jak uznać, że liczba o nieskończonym rozwinięciu, które na dodatek nie jest w żaden sposób okresowe, jest prosta? Pomijam już kwestię praktyczną, bo żeby dokładnie wyznaczyć ten iloraz, trzeba by nieskończenie dokładnie zmierzyć i obwód, i średnicę. Trzeba by mieć nieskończenie dokładną linijkę (jak praktycznie zmierzyć obwód, a nie tylko jego przybliżenie, nawet sobie nie wyobrażam). I – jeśli dobrze rozumiem (jeśli nie, proszę mnie poprawić) – przynajmniej jedna z tych wielkości musi być wyrażona liczbą niewymierną.

No właśnie, może to kwestia wyobraźni. Może jako przyrodnik za bardzo chcę wyobrazić sobie coś namacalnego, i stąd problem. Podobną kwestią mogą być fraktale. W matematyce idą w nieskończoność, ale w gruncie rzeczy są dość proste. Ich kształty nie są losowe, nie są chaotyczne (ani w sensie klasycznym, ani w sensie chaosu deterministycznego, który wydaje się prostszy, bo przynajmniej opisywalny matematycznie). W przyrodzie struktury przypominające fraktale są jednak skończone i koniec końców – mimo pewnej złożoności – proste.

Przywołane spotkanie miało związek z pokazem jednego z filmów Jałochowskiego, który przede wszystkim jest jednak dziennikarzem i ostatnio zrobił serię filmów „Pionierzy” o inspirujących naukowcach. Tym razem był film o Gregorym Chaitinie, informatyku, który chciałby opisać matematycznie biologię, a w szczególności teorię ewolucji. Marzy mu się metabiologia. Ubolewa jednak nad tym, że układy biologiczne – ekosystemy – są bardzo złożone, ale wierzy, że problemy z matematyzacją teorii ewolucji to nie feler tej teorii, tylko cecha wynikająca ze złożoności większej niż ta, z którą informatycy sobie zwykli radzić. Przynajmniej jeśli dobrze go zrozumiałem.

Domyślam się, że nie chce wyważać drzwi otwartych na oścież, bo akurat ekologia i ewolucjonizm to te działy biologii, w których matematykę wprowadza się od wielu lat. I z powrotem – można powiedzieć, że statystyka rozwinęła się bardziej dzięki biologom (zwłaszcza ekologom) i ekonomistom, którzy zawracali głowę matematykom, niż samym matematykom. Dzięki temu Nash mógł dostać nagrodę Nobla, co nieczęsto zdarza się matematykom stroniącym od nauk stosowanych. Nagrodę dostał z ekonomii, ale jego wkład w teorię gier jest też podstawą obecnej wersji teorii ewolucji.

Na spotkaniu przyznałem, że z nazwiskiem Chaitina spotkałem się po raz pierwszy. Tymczasem, przygotowując się do tego wpisu, sięgnąłem na półkę do książki, gdzie jakieś 20 lat temu po raz pierwszy zobaczyłem przykład z łączeniem punktów jako ilustracją złożoności – „Kwarka i jaguara” Murraya Gell-Manna. Tamtejszy przykład jest bardziej złożony, bo ma osiem punktów. Po paru przykładach możliwości rozwleczenia i skondensowania informacji Gell-Mann wprowadza podrozdział „Algorytmiczna zawartość informacyjna”. Tytułowe pojęcie wprowadziło w podobnym czasie trzech matematyków-informatyków. Pierwszy z nich to Andriej Kołmogorow.

Mnie to nazwisko jest znane głównie jako eponim testu statystycznego, którym analizuje się dane. Wbrew podręcznikom dane nie zawsze mają rozkład gaussowski i nie można ich analizować testem t-studenta. Tak było też w przypadku moich badań. Algorytmiczna zawartość informacyjna w ogóle jest znana jako złożoność Kołmogorowa. Dwaj pozostali matematycy nie zostali tak upamiętnieni. Jeden z nich to Ray Salomonoff, a drugi to… Gregory Chaitin.

Zatem wynika z tego, że o Gregorym Chaitinie słyszałem, tzn. czytałem, już dawno temu, a teraz tylko miałem okazję sobie przypomnieć. Czasem warto wrócić do lektur sprzed lat, zwłaszcza że „Kwark i jaguar” to całkiem dobra pozycja na rynku popularyzacji nauki.

Piotr Panek

ilustracja autora, copy left (róbta z nią, co chceta)